|
WARMATHS |
Médiatrice
|
Définition:
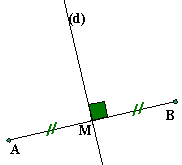
La médiatrice d'un segment est la droite perpendiculaire à ce segment en son milieu.
Propriétés:
|
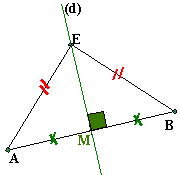
propriété 1: Si un point appartient à la médiatrice d'un segment alors ce point est équidistant des extrémités de ce segment.
|
|
propriété 2:
Si un point est équidistant des extrémités d'un segment
alors ce point appartient à la médiatrice de ce segment.
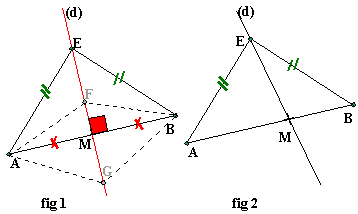
Remarques sur la propriété 2:
Nous pouvons avoir (dans un exercice, un problème) le point E sur une droite (d) avec EA=EB: cela n'est pas suffisant pour affirmer que (d) est la médiatrice de [AB] comme le montre la figure 2 !! Il est nécessaire, pour démontrer cela, que nous ayons un renseignement de plus:
soit un second point de (d) qui soit aussi équidistant de A et B.
soit que (d) est perpendiculaire à [AB].
ou encore que (d) passe par le milieu de [AB] (ce qui revient à avoir un second point équidistant de A et B).
Cette propriété permet:
de démontrer qu'une droite est une médiatrice (vous devrez l'utiliser deux fois pour deux points de la droite).
de tracer le symétrique d'un point par rapport à une droite.
Attention: les propriétés 1 et 2 sont réciproques l'une de l'autre:
Dans la première, nous savons que le point est sur la médiatrice alors que dans la seconde nous n'en savons rien.
Dans la seconde, nous savons que le point est équidistant des extrémités du segment alors que dans la première nous n'en savons rien.
Remarques: La première propriété permet de démontrer qu'un point est équidistant des extrémités d'un segment. La seconde permet de démontrer qu'un point est sur la médiatrice d'un segment.
Construction d'une médiatrice:
Données: le segment [AB].
Pour en construire la médiatrice, nous utilisons deux fois la propriété 2 ci-dessus (revoir les remarques sur cette propriété): détermination de deux points équidistant de A et B avec le compas:
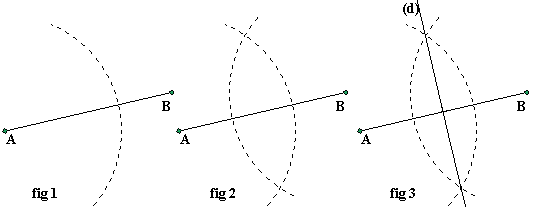
Fig 1: Le rayon donné au compas doit être supérieur à la moitié de AB. Nous traçons un arc de cercle de centre A.
Fig 2: Même chose mais avec B pour centre. Les deux arcs se coupent en deux points (voilà pourquoi il faut que le rayon soit supérieur à la moitié de AB). Comme ces deux points sont équidistants de A et B alors A et B appartiennent à la médiatrice de [AB].
Fig 3: Tracez la droite (d) qui passe par ces deux points. La médiatrice de [AB] est (d).
Remarques: La construction de la médiatrice d'un segment permet:
de trouver très précisément le milieu d'un segment.
de trouver le centre du cercle circonscrit à un triangle.
de tracer une droite perpendiculaire à une droite donnée et passant par un point donné.
Cas de figures:
Vous pouvez rencontrer une médiatrice dans le cas de:
Cercles sécants: La droite des centres est médiatrice de la corde commune.
Cercle circonscrit à un triangle: Le centre d'un cercle circonscrit à un triangle est le point d'intersection des médiatrices des côtés de ce triangle.
Cercle circonscrit à un quadrilatère: pour les rectangles et les carrés voir plus bas. Des trapèzes seul le trapèze isocèle a un cercle circonscrit (dont le centre est l'intersection des médiatrices des deux côtés de même longueur). Sauf cas particuliers, les quadrilatères quelconques n'ont pas de cercle circonscrit.
|
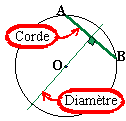
Médiatrice d'une corde: elle passe par le centre du cercle (comme OA=OB=rayon alors O appartient à la médiatrice de [AB]. Diamètre perpendiculaire à une corde: Un diamètre perpendiculaire à une corde d'un cercle est médiatrice de cette corde. Pour démontrer cette propriété voyez les remarques sur la propriété 2. Diamètre passant par le milieu d'une corde: ce diamètre est la médiatrice de cette corde (à démontrer...). |
|
Symétrie orthogonale: L'axe de symétrie est médiatrice du segment dont les extrémités sont un point et son image.
Rectangles et carrés: Ces figures ont pour axe de symétrie les médiatrices (qui sont aussi les médianes) des côtés. L'intersection de ces axes est le centre du cercle circonscrit.
![]() © Lallet Gérard 1998
© Lallet Gérard 1998
|
[Accueil] |