|
WARMATHS |
Hauteur et Orthocentre |
- Définitions. : « hauteur » ;
« orthocentre »
- Cas particuliers:
Hauteur : Une hauteur d'un triangle est une
droite qui passe par un sommet et est perpendiculaire au côté opposé.
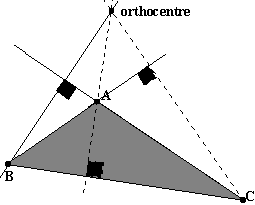
Orthocentre :
Les trois hauteurs d'un triangle se coupent en un point (elles sont
concourantes en ce point) appelé orthocentre.
Dans un triangle le mot
"hauteur" désigne aussi la distance d'un sommet au côté opposé. Ce côté est alors appelé
la base du triangle. Il faut bien voir qu'il y a trois bases possibles
dans un triangle, comme il y a trois hauteurs et donc trois façons de calculer
l'aire d'un triangle
Tracés:
-d'une hauteur: voir le tracé d'une
droite perpendiculaire à une droite donnée et passant par un point donné.
-de l'orthocentre: il suffit
de tracer deux hauteurs. Leur intersection est le point cherché.
|
Remarque: La hauteur issue d'un sommet d'un
triangle peut se trouver entièrement à l'extérieur de ce triangle. C'est le
cas lorsqu'il y a un angle obtus dans le triangle (c'est le seul angle obtus
du triangle d'ailleurs). L'orthocentre est alors aussi à l'extérieur
du triangle; |
|
Cas
particulier du triangle rectangle:
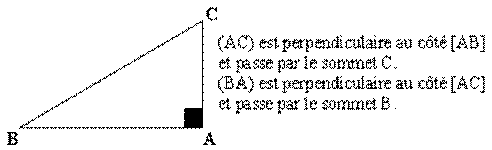
Dans un triangle rectangle
deux côtés sont perpendiculaires. Chacun de ces deux côtés passe par un sommet
et est perpendiculaire au côté opposé. Nous avons donc déjà deux hauteurs qui
se coupent au sommet de l'angle droit. L'orthocentre est donc ce sommet.
Cas
particulier du triangle équilatéral:
Dans un triangle équilatéral,
les hauteurs sont aussi les médianes,
les médiatrices des côtés et
les bissectrices des angles.
L'orthocentre d'un triangle équilatéral est donc aussi le centre de gravité, le centre du cercle inscrit et du cercle circonscrit.