Le cône droit

Définitions:

Le cône droit (ou cône de révolution) est un solide de révolution.

Le cône droit est engendré par la révolution d'une ligne polygonale SAO ( le profil) telle que l' angle en SOA est droit, autour de (SO). L'axe de révolution est la droite (SO).

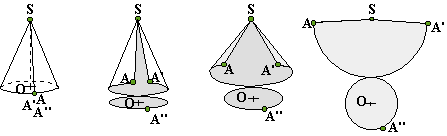
fig 1: Représentation du profil en noir et de l'axe de révolution en vert .

fig 2: Vue de dessous. Dessinées en pointillés, quelques positions du profil sont représentées. La rotation autour de l'axe (SO) se fait ici, dans le sens des aiguilles d'une montre (indiqué par une petite flèche rouge).

fig 3: Le cône est représenté par 16 positions du profil. Les faces ont été constituées par des petits morceaux de plan (facettes).

fig 4: Toutes les positions du profil ont été représentées. Comme il y en a une infinité, les 2 faces du cône sont chacune en un seul morceau.

Remarques:

-Au lieu de prendre la ligne polygonale SAO nous pouvons n'utiliser que le segment [SA] (profil générateur). Le point A décrit un cercle de centre O et de rayon OA. Dans ce cas nous obtenons un cône droit sans matérialisation de la base (il s'agit d'un cornet droit).

-La partie [AO] du profil décrit un disque de centre O et de rayon OA.

-L'axe de rotation est perpendiculaire au plan engendré par la droite (OA).

-Le profil est appelé génératrice.

Propriétés:

Le cône droit possède 2 faces:

-Une face de base: disque (ou cercle) dont le centre O est sur l'axe de révolution (axe autour duquel tourne le profil ou génératrice) et de rayon R.

-Une face latérale dont la forme développée (vue à plat) est étudiée au paragraphe Patron.

Par construction, l'axe (SO) autour duquel tourne le profil est un axe de symétrie pour le cône droit.

L'axe (SO) est perpendiculaire au plan de la base.

Patron:

Un patron est une figure dessinée sur un plan. Elle permet de façonner un objet qui représente le solide dans l'espace.

Les trois premières figures ci-dessous essaient de représenter le "dépliage" du cône droit en utilisant la perspective cavalière. La dernière figure représente le patron d'un cône droit.

Exercice: construire le patron du cône droit dont la génératrice SAO est composée du segment [SA] de longueur 6cm et du segment [OA] (rayon de la base) de longueur 2cm. Ne pas oublier une languette le long de [SA] pour le collage (deux filets de colle rapide sur l'arc [AA'] devraient suffire pour la fixation du disque).

Calculs: le patron est constitué d'un disque de rayon r=2cm et d'un secteur de disque de rayon R=SA=6cm. Ce qu'il faut calculer c'est l'angle au centre ASA'.

Angle

centre(°)

Longueur

l'arc(cm)

360

2.pi.R

2.pi.r

Figure à l'échelle 1/2

Si nous gardions tout le disque de rayon R l'angle au centre aurait pour mesure 360° et le périmètre serait 2.pi.R. Nous ne gardons que le secteur d'angle au centre de mesure inconnue a et dont la longueur de l'arc est égale au périmètre du disque de base 2.pi.r (comme le bord du disque doit être collé sur le bord du secteur il faut qu'ils aient la même longueur). Il s'agit d'un calcul de proportionnalité: la longueur du bord du secteur (appelé arc de cercle) est proportionnelle à l'angle au centre qui sous-tend cet arc.

Utilisons l'égalité des produits en croix:

a.2.pi.R=2.pi.r.360

En multipliant les deux membres de cette égalité par l'inverse de 2.pi.R (c'est à dire par 1/2.pi.R: voir résolution des équations) nous obtenons:

a=(2.pi.r.360)/(2.pi.R)

Après simplification par 2.pi:

a=r.360/R ou a=360.r/R

Avec les données de notre exemple, l'angle au centre est 360.2/6 soit 120°.

Sections planes:

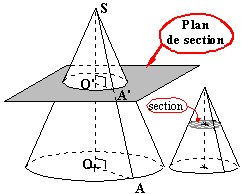
Une section plane d'un cône est obtenue en coupant le cône à l'aide d'un plan. Sur les figures de ce chapitre, le plan utilisé est représenté par un parallélogramme colorié en gris afin de donner une impression de relief. Les lignes cachées sont représentées en pointillés.

- parallèlement à la base:

La section d'un cône droit par un plan, parallèlement à la base du cône est un disque (cercle si nous avons un cornet) de rayon plus petit que celui du disque (cercle) de base.

Ce rayon dépend de la distance SO' de S au plan de section.

Les triangles SOA et SO'A' sont rectangles respectivement en O et O'. Les droites (OA) et (O'A') sont dans le même plan (celui contenant les points S, O et A) et sont perpendiculaires à la droite (SO). Les droites (OA) et (O'A') sont donc parallèles.

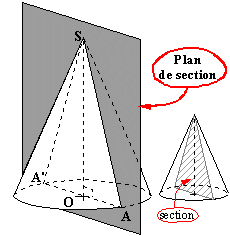
-passant par l'axe de symétrie (SO):

La section d'un cône droit par un plan passant par l'axe de symétrie (SO) du cône, est un triangle isocèle de sommet principal le sommet S du cône et dont la base principale a pour longueur le diamètre de la base du cône.

Sur la figure ci-contre:

SAA' est isocèle en S. [AA'] est un diamètre du disque de base du cône. Nous avons: SA=SA' et (SO) est médiatrice de [AA'].

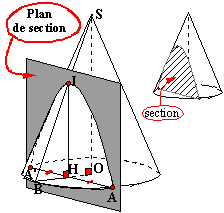
-parallèlement à l'axe de symétrie: (pour info: n'est pas au programme du collège)

La section d'un cône droit par un plan parallèle à l'axe de symétrie est une surface limitée par une corde du disque de base et un arc d'une courbe appelée hyperbole.

Sur la figure ci-contre:

-A, I et A' sont des points de l'hyperbole. Le triangle AIA' est isocèle de sommet principal I.

-(IH) perpendiculaire au plan du disque de base, coupe [AA'] en son milieu, (OH) est donc médiatrice de [AA'] (c'est un diamètre du disque de base, passant par le milieu d'une corde)

Formules:

On sait que l'aire d'un secteur circulaire est donné par la formule (pi.R².a)/360 où R est le rayon du secteur et a l'angle au centre (nous remplacerons dans cette formule R par L dans la suite de ce document).

Nous avons vu, lors de l'étude du patron du cône, que l'angle au centre a du secteur circulaire (face latérale du cône) est donné par a=360.(R/L) où R est le rayon du disque de base et L le rayon du secteur circulaire représentant la face latérale.