Warmaths :

Résumé « collège »

Conversions

Unités de mesures:

de longueurs
d'aires et agraires
de volumes
de masses
de capacités
d'angles
de durées
de vitesse

1. Unités de longueur:

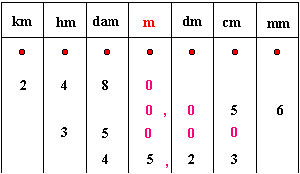
L'unité de mesure des longueurs est le mètre noté M ou m. Le tableau ci-dessous représente les multiples (kilomètre-km- hectomètre-hm- décamètre-dam-) et les sous-multiples (décimètre-dm- centimètre-cm- millimètre-mm-) du mètre.

Le point rouge, dans chaque colonne signifie que vous ne pouvez mettre qu'un chiffre par colonne. Le premier chiffre à placer dans ce tableau (comme dans les autres) est celui qui indique l'unité utilisée ( dans 12,569m, c'est le 2 qui exprime l'unité utilisée, le mètre, et non pas le 9; c'est donc le 2 qui est placé le premier dans la colonne des mètres). Exemples de conversions:

Convertir 248dam en mètres: le chiffre 8 indique le nombre de décamètres. Ce chiffre est placé dans la colonne des dam et les chiffres de gauche sont placés dans les colonnes à gauche de celle du 8. Il suffit de mettre le zéro manquant (en rouge dans le tableau) pour trouver 248dam=2480m.

Convertir 56mm en mètres. Le 6 de 56 doit être placé dans la colonne des millimètres avec le 5 à sa gauche. Pour obtenir les mètres, il faut mettre des zéros dans les colonnes vides à gauche du 5 jusque dans la colonne des mètres et mettre une virgule à droite de ce dernier zéro. Le résultat est: 56mm=0,056m. Attention à bien placer la virgule..
Convertir 3,5hm en centimètres. Le premier chiffre à poser est le 3 dans la colonne des hectomètres: car il s'agit de 3hm.Le 5 est placé à sa droite, dans la colonne des décamètres. Les zéros remplissent les colonnes vides jusqu'à celle des centimètres. Pas besoin de virgule ici puisqu'à droite de la colonne des centimètres il n'y a aucun chiffre. D'où: 3,5hm=35000cm.
Convertir 452,3dm en mètres. Le 2 doit être mis dans la colonne des décimètres. Les autres chiffres se placent dans les colonnes à gauche (pour le 4 et le 5) et à droite (pour le 3). Une virgule doit être mise à droite du chiffre qui se trouve dans la colonne des mètres, donc à droite du 5 et nous avons le résultat: 452,3cm=45,23m.

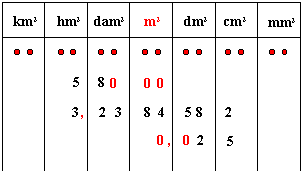
2. Unités d'aires:

L'unité d'aire est dérivée de celle des longueurs puisque nous calculons une aire en manipulant des longueurs (longueurs de côtés, de rayons,..). Il s'agit du mètre carré (symbole: m²). Cette unité représente l'aire d'un carré de 1m de côté. Les multiples sont : le décamètre carré (dam²), l'hectomètre carré (hm²) et le kilomètre carré (km²). Les sous multiples sont: le décimètre carré (dm²), le centimètre carré (cm²) et le millimètre carré (mm²). Dans chaque colonne du tableau ci-dessous, deux points rappellent qu'il faut mettre deux chiffres dans chaque colonne. Pour placer 218,6dm², il faur d'abord écrire le 8 dans la colonne des décimètres carrés et le 1 à la gauche du 8 dans la même colonne; le 2 se retrouve alors sur la droite de la colonne des mètres carrés et le 6 sur la gauche de la colonne des centimètres carrés. Pour convertir 218,6dm² en centimètres carrés il faudrait donc ajouter un 0 à droite du 6 dans la même colonne ( d'où: 218,6dm²=21860cm² et aussi 218,6dm²=2,186m²,...). Autres exemples de conversions:

Mettre 5,8hm² en mètres carrés: mettre le 5 sur la droite de la colonne des hectomètres carrés, placer le 8 et ajouter un nombre de 0 (en rouge dans le tableau ci-contre) tel qu'il y ait deux chiffres par colonne, jusque dans celle des mètres carrés. On obtient:
5,8hm²=58000m².
Convertir 323,84582dam² en hm². Dès que le 3 est convenablement placé, il suffit de lire la réponse:
323,84582dam²=3,2384582hm²
Ecrire 2,5dm² en mètres carrés. Il manque des chiffres à gauche du 2 pour remplir les colonnes jusqu'aux mètres carrés. Il suffit d'ajouter des 0 à gauche du 2. On trouve:
2,5dm²=0,025m²

Unités agraires: dans l'agriculture d'autres unités d'aire sont utilisées. L'unité de base est l'are(a) qui ne possède qu'un seul multiple l'hectare(ha) et qu'un seul sous multiple le centiare(ca). Les équivalences avec les mesures d'aire du tableau sont:

1are=100m² ; 1hectare=100ares=10000m² ; 1centiare=1m²

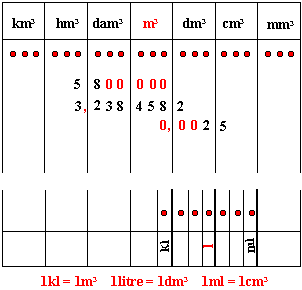
3. Unités de volumes:

L'unité est dérivée de celle des longueurs puisque nous calculons un volume en manipulant des longueurs (longueur de côtés, de rayons,..) et des aires (aires de base diverses). Il s'agit du mètre cube (symbole: m³). Cette unité représente le volume d'un cube de 1m d'arête. Les multiples sont : le décamètre cube (dam³), l'hectomètre cube (hm³) et le kilomètre cube (km³). Les sous multiples sont: le décimètre cube (dm³), le centimètre cube (cm³) et le millimètre cube (mm³). Dans chaque colonne du tableau ci-dessous, trois points rappellent qu'il faut mettre trois chiffres dans chaque colonne. La technique de conversion est toujours la même: il faut placer d'abord le chiffre des unités sur la droite de la colonne correspondante. Exemples:

5,8 hm³ à convertir en mètres cubes. Il faut ajouter des 0 de façon à cequ'il y ait trois chiffres par colonne jusque dans celle des mètres cubes. On a:
5,8 hm³= 5 800 000m³
Rien de plus facile pour convertir 3238,4582dam³en hectomètres cubes. La virgule se place dans la colonne des hectomètres cubes, à droite.
Pour convertir 2,5dm³ en mètres cubes, il faut ajouter à gauche les 0 nécessaires pour aller jusque dans la colonne des mètres carrés.

Remarques: Les unités de volumes expriment des mesures beaucoup plus grandes que celles de capacité. Sous le tableau des volumes j'ai placé le tableau réduit des unités de capacités pour mettre en évidence les équivalences

4. Unités de masse: L'unité de mesure des masses est le gramme noté G ou g. Le tableau ci-dessous représente les multiples (kilogramme-kg- hectogramme-hg- décagramme-dag-) et les sous-multiples (décigramme-dg- centigramme-cg- milligramme-mg-) du gramme. Son utilisation est la même que pour celui des longueurs ci-dessus.

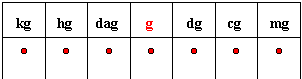
remarque: Dans l'industrie et le commerce la tonne (T) et le qintal (q) sont aussi utilisés avec les correspondances suivantes:

1T=10q 1T=1000kg et 1q=100kg

5. Unités de capacités: L'unité de mesure des capacités est le litre noté L ou l. Le tableau ci-dessous représente les multiples (kilolitre-kg- hectolitre-hg- décalitre-dag-) et les sous-multiples (décilitre-dg- centilitre-cg- millilitre-mg-) du litre. Son utilisation est la même que pour ceux des longueurs et des masses ci-dessus. Attention: ne pas confondre avec les unités de volumes dont le tableau permet l'introduction de trois chiffres par colonne.

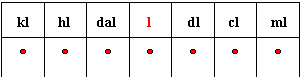
6. Unités d'angles:

L'unité d'angle est le Droit; elle est notée D. C'est la mesure de l'angle ...droit! Jusque là c'est très simple. Mais il faut reconnaître qu'un angle mesurant 1D est déjà un grand angle. Aussi existent-ils des sous multiples et c'est là que tout se complique...

L'unité sous multiple du Droit la plus utilisée en quatrième est le degré et ses sous multiples.

a) Le degré:

Par définitions:

· Il y a 90 degrés dans un Droit. Ce qui s'écrit: 1D=90°.

· Il y a 60 minutes d'angle dans un degré. Soit: 1°=60' (remarquez bien la petite virgule en haut derrière 60, ce qui exprime les minutes d'angle et 60' se lit 60 minutes d'angle ou 60 minutes si on ne peut pas confondre avec une durée). Remarque: 1'=1°/60 ou 1/60 de degré

· Il y a 60 secondes d'angles dans une minute d'angle. Soit: 1'=60" (deux petites virgules en haut cette fois, pour les secondes d'angle). Donc: 1°=60 x 60=3600" (60' valant chacune 60"). Remarque: 1"=1°/3600 ou 1'/60.

Exemples: 45°20'50" soient 45x3600 + 20x60 + 50 = 163250" . La manipulation de ces unités se fait comme avec les unités de durée.

En général nous n'utilisons pas les sous multiples du degré (écriture sexagésimale). Nous préférons utiliser une écriture décimale.Par exemple: 30,5° ce qui ne signifie pas 30° et 5 minutes d'angle mais 30° et 0,5°=0,5 x 60= 30' , finalement: 30,5°=30°30'

Autres exemples:

45,8° (remarquez bien que le symbole ° est placé complètement à droite du nombre et non pas après 45) à convertir en écriture sexagésimale: 45,8°=45°+0,8° où 0,8°=0,8x60'=48'. Donc: 45,8°=45°48'.

Convertir 25°50' en écriture décimale. En fait il faut convertir 50' en degré. Comme 1'=1°/60 alors 50'=50x1°/60 ou 50'=50°/60 ou 50'=0,833333...° arrondi à 0,83° (après avoir effectué la division de 50 par 60); Nous obtenons: 25°50'=25,83°.

b) Les autres sous multiples du Droit:

- Le grade: il y a 100 grades dans un Droit. Le grade se note: gr (ne pas confondre avec le gramme!...). L'écriture des mesures d'angles en grade est une écriture décimale. On utilise sourtout les sous multiples du grade: le décigrade (dgr), le centigrade (cgr) et le milligrade (mgr). Les conversions se réalisent comme pour les longueurs, les masses ou les capacités.

-Le radian: non utilisé en quatrième mais vous sera très utile dans certains calculs.. plus tard dans vos études.

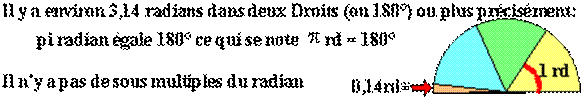
1 radian

c) Opérations sur les mesures d'angles: elles s'effectuent de la même manière qu'avec les unités de durée (paragraphe suivant). Vous remplacerez les heures par les degrés (°), les mn par ' et s par " .

7. Unités de durées:

Les unités de durée mesure le temps qui passe. L'unité de base est l'heure (h). Les sous multiples en sont la minute (mn) et la seconde (s). Ici, comme pour les mesures d'angles en degrés, il s'agit d'écritures sexagésimales. Les conversions se font de la même façon. Nous donnons ci-dessous quelques exemples de calcul avec ces unités.

Il faut ajouter, retrancher ou multiplier les nombres dans chaque colonne ( heures, minutes, secondes) sans faire de reports (retenues faites lors de calculs sur des nombres décimaux). Les résultats obtenus sont convertis dans l'unité immédiatement supérieure si ils sont supérieurs à 60 pour les minutes et le secondes. Vous pouvez convertir un nombre d'heures supérieur à 24, en jours.

Dans les exemples ci-dessous, les calculs présentés en bleu sont des calculs intermédiaires qu'il est parfois inutile d'écrire (vous barrez proprement et vous remplacez directement dans l'opération).

Addition: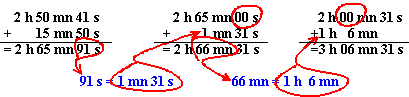

Soustraction: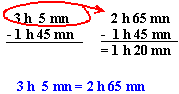

Multiplication (par un décimal):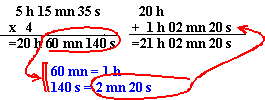

Division (par un nombre sexagésimal):dans ce cas le résultat est un nombre sans unité (c'est à dire, ici, simplement un nombre de fois 3h15mn dans 20h45mn)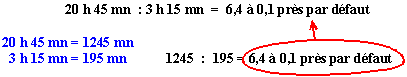

Division (par un décimal):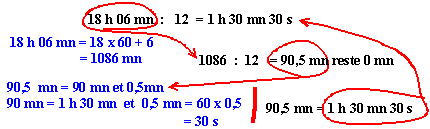

8. Unités de vitesses:

La vitesse moyenne d'un mobile est définie comme étant la distance parcourue par unité de temps. L'unité de vitesse dépend des unités choisies pour la distance (=longueur) et le temps (=durée). Si la distance est en centimètres et la durée en secondes ou en heures.. la vitesse est en cm.s ou cm.h,.. (centimètres par seconde ou centimètres par heure,...)

Si le mobile parcourt 10000m en 20mn alors sa vitesse est le nombre de mètres parcourus pendant une seconde soit 10000:20=500m.mn ce qui se lit 500 mètres minute. Pour obtenir la vitesse de ce mobile en kilomètres heure il faut convertir 10000m en kilomètres soit 10km, et 20mn en heure, soit: 20x1/60d'heure (car 1mn=1h:60), et 20/60 d'heure=0,33h environ (effectuez la division de 20 par 60). D'où la vitesse est 10:0,33=30km.h environ.

Remarques:

1.dans l'exemple précédent la durée de 20mn est un cas intéressant puisqu'il y a 3 fois 20mn dans une heure. Si le mobile parcourt 10km en 20mn, il va parcourir 3 fois 10km en 1h. Sa vitesse est donc 30km.h exactement. Cependant la méthode précédente est plus générale (elle fonctionne dans tous les cas). Pour les cas particuliers, le calcul est évidemment plus rapide et plus précis (il y a bien une division mais le résultat est exact et non pas du style 0,333333...!) et la méthode fonctionne très bien pour toutes les durées sous multiples de 60 ( 2, 3, 4, 5, 6, 10, 12, 15, 20, 30).

2. En fait il existe une formule pour calculer la vitesse moyenne. De cette formule, en utilisant les propriétés des quotients égaux, nous pouvons extraire une formule pour calculer la durée et une autre pour calculer la distance:

où: v exprime la vitesse, d la distance et t la durée. Attention de bien associer les unités dans les formules. C'est la cause la plus fréquente d'erreurs: ne mettez pas, par exemple, la vitesse en mètres.seconde avec une distance en kilomètres ou une durée en heures...