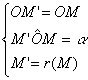DOC. : Professeur ; Formateur

DOC : Formation Individualisée

DOC : Elève.

COLLEGE : RESUME en GEOMETRIE PLANE

TRANSITION / COLLEGE / LYCEE.

Information « TRAVAUX » Cliquer sur le mot !.

INFORMATIONS PEDAGOGIQUES :

NIVEAU : GEOMETRIE PLANE Formation Niveau V

OBJECTIFS : - Savoir

I ) Pré requis:

i9

La géométrie plane (lecture)

:i

II ) ENVIRONNEMENT du dossier :

Index

Dossier précédent : PROPRIETE et réciproque DE THALES.

Dossier suivant :

Info :retour vers liste des résumés. i9 les transformations en géométrie.

III) LECON Rappels sur : GEOMETRIE PLANE (partie 1)

Chapitres :

i9	TITRE :	:i
i9	1. TRANSFORMATIONS USUELLES. Symétrie orthogonale/ symétrie centrale/Rotation/Translation.	:i
i9	2. COMPOSITION DE TRANSFORMATIONS.	:i
i9	3. ENSEMBLES INVARIANTS PAR SYMETRIE	:i
i9	4. AIRES	:i

IV) INFORMATIONS «  formation leçon » :

Test	RESUME	Travaux auto - formation.			Corrigé des travaux auto - formation.
		Contrôle	évaluation	INTERDISCIPLINARITE	Corrigé Contrôle	Corrigé évaluation

V ) DEVOIRS ( écrits) : à venir !!!

Devoir diagnostique L tests.	Ÿ
Devoir Auto - formatif (intégré au cours)	Ÿ
Devoir Formatif « Contrôle : savoir » ; (remédiation)	Ÿ
Devoir Formatif «  Evaluation  savoir faire » (remédiation)	Ÿ
Devoir sommatif.	Ÿ
Devoir certificatif : (remédiation)	Ÿ

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

Leçon	Titre
N°	GEOMETRIE PLANE :LES TRANSFORMATIONS

RESUME

i9

1°) TRANSFORMATIONS USUELLES.

:iAprès

Avant

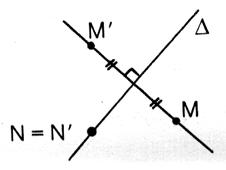
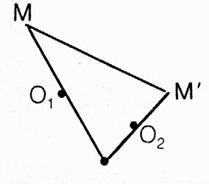
Symétrie orthogonale (notée :)

Après

Si le point M et le point M' sont symétriques par rapport à la droite "delta" (D) , cela signifie que (D) est la médiatrice du segment [MM'] On note M' = (M) et M = (M') . Si NÎ D , alors N'=N La droite D est l'ensemble des points "invariants" par la symétrie orthogonale

i9

Symétrie centrale

:i

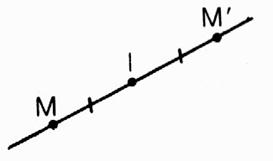
Si M et M' sont symétriques par rapport à I , cela signifie que le point I est le milieu du segment [MM'] M' = [M] et M = [M'] , I = (I) Le point I est son propre symétrie. C'est le seul point invariant dans la symétrie ce centre "I". Il s'agit du centre de symétrie.

Avant :secteur angulaire

Rotation

Après : en plus

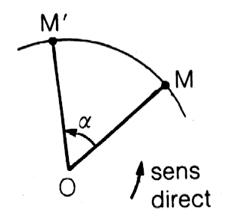
On dira que M' est le transformé de M par rotation "r" de centre "O", et d'angle a , ce qui signifie : Le point O est son propre transformé, il est le "centre" de la rotation, c'est le seul point invariant.

Avant

Translation

Après

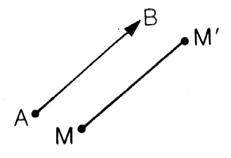
Le point M' est le "transformé" de M par la translation de vecteur AB ( ) Cela signifie que = . On note M' = (M) Si ¹ , il n'y a aucun point invariant.

Propriétés des transformations.

Les quatre transformations conservent :

·Les distances, l'alignement, les angles, les aires, le parallélisme, la perpendicularité.

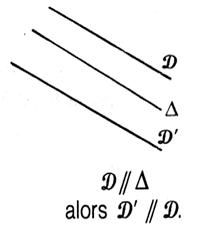
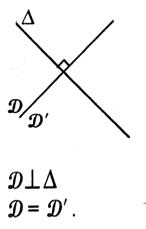
* L'image d'une droite est une droite.

Ainsi :

- Elle est parallèle à elle même dans la symétrie centrale et dans une translation.

- Dans une symétrie orthogonale par rapport à "delta" nous avons l'image des droites :

· L'image d'un cercle C (O,r) est un cercle C' ( O',r) , le point O' étant l'image de O.

i9

COMPOSITION DE TRANSFORMATIONS

:i

· Suite de deux symétries orthogonales : suivie de

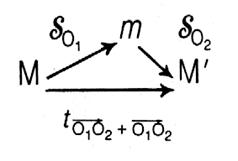
	On remarquera que la composée de deux symétries orthogonales est aussi la symétrie centrale de centre "O"
Remarquer que l'ordre de la composition n'intervient pas quant au résultat obtenu.

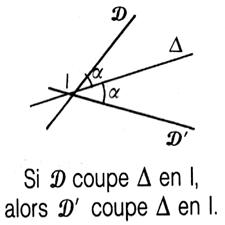
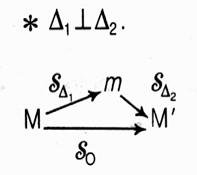
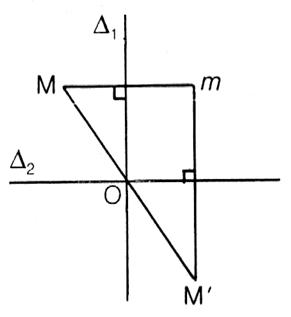
· D 1 // D2 · On trace la double symétrie du point M ; on obtient successivement "m" et "M'" image de "m" par rapport à la droite D2 La composée des symétries suivie de est une translation. Dans ce cas : L'ordre dans lequel s'effectue les symétries intervient.

· Suite de deux symétries centrales : suivie de

	On réalise une double symétries centrales; on obtient d'abord l'image "m" de "M"puis l'image "M" " image de "m".
	m

i9

ENSEMBLES INVARIANTS PAR SYMETRIE

:i

¨Une droite delta (D) du plan est un axe de symétrie d'une figure "F" si et seulement si "F" coïncide avec son image "F' " dans la symétrie orthogonale d _D

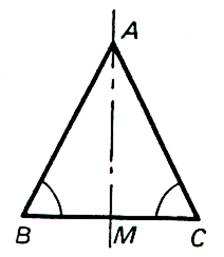
Exemple 1 :

Triangle isocèle: Possède: · un axe de Symétrie AM

¨Un point "O" du plan est un centre de symétrie d'une figure "F" si et seulement si " F " coïncide avec son image " F' " dans la symétrie centrale d _O

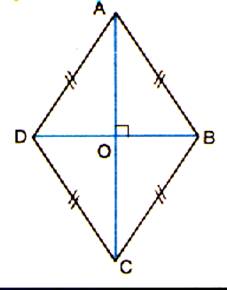
Exemple 2:

Le losange. Possède: · deux axes de symétrie: AC et BD · Un centre de symétrie. "O"

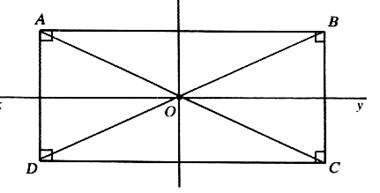
D₂

Exemple 3:

Le rectangle: Possède: · deux axes de symétrie: D1 et D2 · Un centre de symétrie. "O"

D1

Un point "O" du plan est un centre de symétrie d'une figure "F" si et seulement si " F " coïncide avec son image " F' " dans la symétrie centrale d _O

Exemple 4:

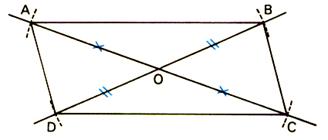
Le parallélogramme. possède: · Un centre de symétrie. "O"

Exemple 5

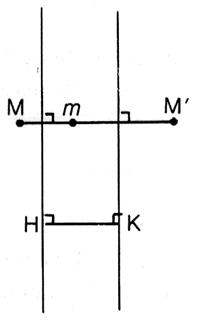
La bande de plan. La droite D est l'axe de symétrie qui "échange" D1 et D2 Toutes les perpendiculaires communes à D1 et D2 sont des axes de symétrie laissant D1 et D2 invariantes.

D1 D2 D2

Exemple 6

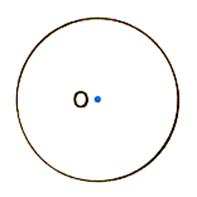
Le cercle : ·Le cercle admet un centre de symétrie, son centre « O ». · toutes droites diamétrales sont axes de symétrie.

i9

AIRES

:i

On retiendra essentiellement la formule concernant l’aire du triangle et celle du disque.

· L’aire d’un triangle ABC, de hauteur AH :

· Aire du disque de rayon R . S = p R²

Leçon	Titre
N°	TRAVAUX d ’ AUTO - FORMATION sur LES TRANSFORMATIONS USUELLES.

Voir cas par cas.

TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE

TRAVAUX N° d ‘ AUTO - FORMATION EVALUATION