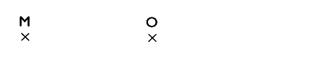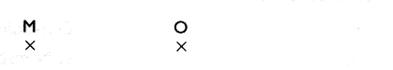|
Auteur :
WARME R.
Document
« élève ».
|
||||||||||||||||||
|
NOM : ……………………………… |
Prénom : ………………………….. |
Classe :………………….. |
||||||||||||||||
|
Année scolaire : ……………………… |
Dossier
pris le : ……/………/……… |
Validation
de la formation : O -
N Le : …………………………………….. Nom
du formateur : …………………… |
||||||||||||||||
|
ETABLISSEMENT :
………………………………………….. |
||||||||||||||||||
|
Leçon |
||||||||||||||||||
|
N°16 |
L ' axe de symétrie et SYMETRIE CENTRALE ;
« orthogonalité » , « centre de symétrie » et SYMETRIE ORTHOGONALE |
|||||||||||||||||
|
CHAPITRES : |
||||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|||||||||||||||
|
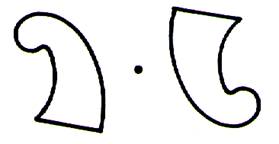
Ne pas
confondre symétrie centrale et symétrie
orthogonale
|
|
||||||||||||||||
|
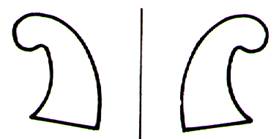
Symétrie centrale : le point est centre de symétrie. |
Symétrie orthogonale : la droite qui sépare les
figures est axe de symétrie. |
|
|||||||||||||||
|
F’ F |
|
|
|||||||||||||||
|
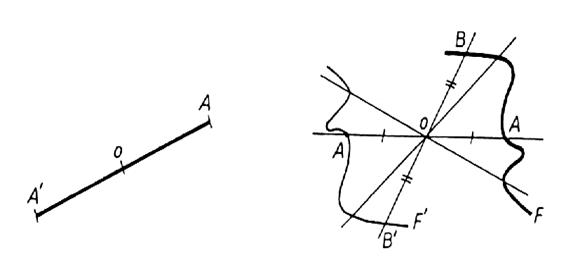
Imaginer la figure F liée au centre ; F’ est la
position de F après une rotation de 180° , ( penser au manège) |
Reproduire avec une feuille de calque et constater qu’après pliage (
suivre l’axe de symétrie ) et remarquer que les deux figures se superposent . |
|
|||||||||||||||
|
|
|||||||||||||||||
|
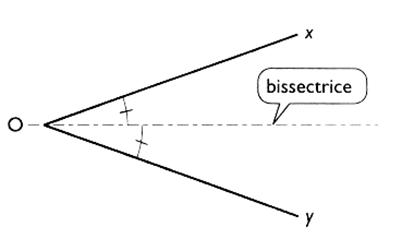
Par
définition : la bissectrice et
la médiatrice sont appelées aussi : « axe de
symétrie » : uLa bissectrice est l' axe de
symétrie d'un angle |
|
||||||||||||||||
|
|
|
||||||||||||||||
|
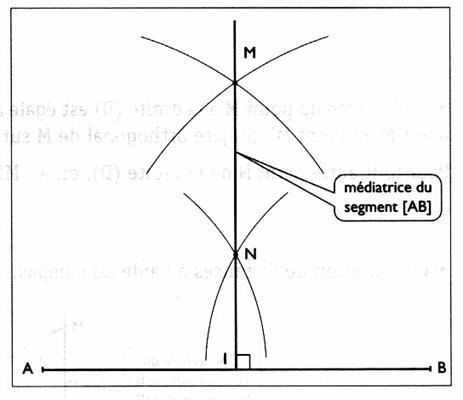
v La médiatrice
d'un segment est l'axe de symétrie de ce segment .
|
|
||||||||||||||||
|
w Lorsqu'une figure est conservée par une
symétrie orthogonale d ' axe ( D ) , elle
admet cette droite ( D ) comme axe de symétrie
.
|
|
||||||||||||||||
|
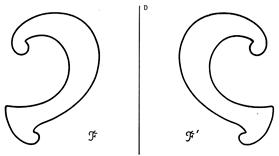
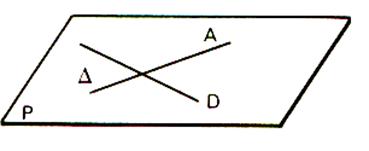
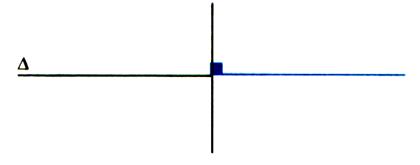
² On dira
que : Dans
une symétrie orthogonale par rapport à une droite « delta » , la
droite « delta » est appelée « axe de symétrie » Activité : Joignez les points pour obtenir le « symétrique : F’ » de la figure « F » .
|
|
||||||||||||||||
|
|
|||||||||||||||||
|
u centre
de symétrie entre deux points : —Activité
: Avec une
règle tracer une droite passant par M
et O . a) Mesurer la distance [MO] avec un compas . b) Reporter le point "N" tel que "O"
soit le milieu du segment [MN].
|
|
||||||||||||||||
|
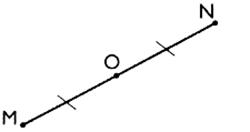
Commentaire : On dit que les deux points
M et N sont symétriques par rapport au point O lorsque le point O est
le milieu du segment [MN]. |
Résultat : Le point "O" est le centre de symétrie
; le point "N" est l ' image
du point " M" dans la symétrie de centre "O" . |
|||||||||||||||||
|
|
||||||||||||||||||
|
vLe centre
de symétrie de figures
géométriques : |
||||||||||||||
|
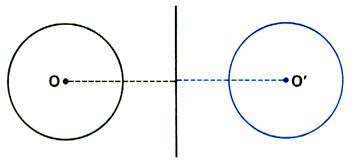
le centre du cercle est centre de symétrie |
le centre du cercle est
centre de symétrie du polygone. |
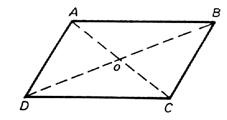
Parallélogramme ( et losange –rectangle- carré) . Le point de
rencontre des diagonales est centre de symétrie. |
||||||||||||
|
|
||||||||||||||
|
w le
centre de symétrie d’une figure quelconque « F ». « O »
est le centre de symétrie ; observer la figure , et constater qu‘il faut décomposer la ligne en une
« infinité » de points qui font individuellement l’objet
d’une symétrie centrale .
|
||||||||||||||
|
|
||||||||||||||
|
III )
TRACES des éléments de base en SYMETRIE CENTRALE. |
|
||||||||||||
|
1°) Savoir tracer le
symétrique d’un point par rapport à un autre point . Activité : Construire « P », le symétrique de M par rapport à
"O" Procédure : tracer une droite passant
par M et 0 .
Avec un compas , prendre l’écartement
de O à M , conserver la pointe
en 0 et tracer un trait
coupant la droite , à l’opposé de M , pour obtenir le point P ; tel que le point "O" soit le
milieu du segment MP.
|
|
||||||||||||
|
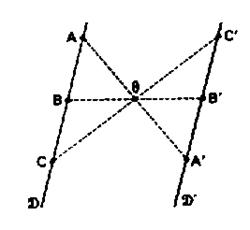
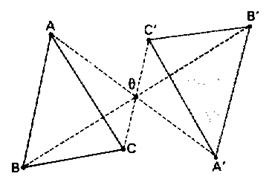
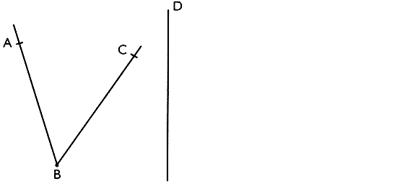
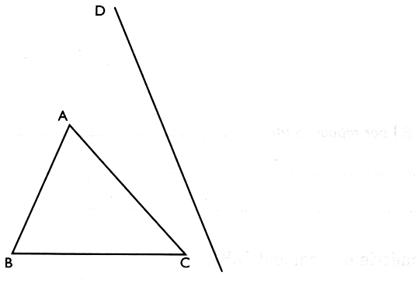
2° ) Savoir construire le symétrique du
segment AC , noté [AC ] par rapport à "O". Procédure : - Construire le point "A '
" avec la règle et le
compas ; tel que le point
"O" soit le milieu du segment A A '. -
Construire le
point "C ' "
avec la règle et le compas ;
tel que le point "O" soit le milieu du segment CC '. -
Tracer le segment A ' C ' . ( noté [A’C ’]
) On dira que : le segment [A ' C ' ] est appelé le symétrique du segment [A C ] l Remarque : si le point
B appartient au segment AC ; on
remarquera que le point B’
appartient au segment A’
C’ . L’alignement des points est conservée . |
|
||||||||||||
|
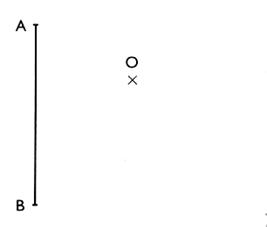
Activité : tracer
le symétrique de [ AB ] par rapport au point O .
? Vérification : On
peut vérifier qu’il y a parallélisme
entre les segments et qu’ils sont de même longueur : Il faut vérifier que [A ' C' ] est parallèle à [A C ] . Rappel de 2 méthodes qui permettent de vérifier si deux côté sont
parallèles : i 1 : si C , A
, C’, A’ forment un
parallélogramme , le point
« O » est le point
d’intersection des diagonales , elles se coupent en leur milieu . On
vérifie si A O =
OA’ et si CO = O’ C’ i 2 :
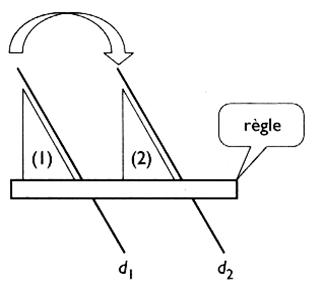
Méthode : Un bord de
l'équerre coïncide avec la
droite " d 1"; On fait glisser l'équerre sur la règle
(qui conserve une direction fixe ) en passant de (1) à la position ( 2). Les
droites "d1" et " d2" matérialisées
par le bord de l' équerre sont parallèles si
la droite " d 2" coïncide avec le bord de l'équerre .
et l’on vérifie avec le compas que les longueurs
A'C' et AC sont égales. Puisque dans un parallélogramme les côtés doivent être parallèles et égaux deux à deux , on vérifiera que les côté A C’ et C A’
sont // et de même longueur . · Pour faire la symétrie centrale d’une droite on fait la symétrie d’un de ses segments : A _ : la symétrie de la droite ( A C ) , droite portant le segment AC , est la droite ( A ' C ' ) , droite
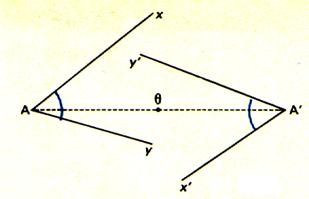
portant le segment A' C' . 3 ° ) Savoir construire le symétrique de l'angle
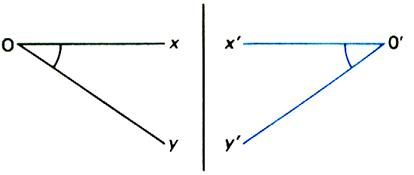
par rapport à un point : ( voir CD ) · Le point A ’ et les demi - droites y’ A’ et
x’ A’ forment le symétrique de
l’angle de sommet A par rapport
au point q .
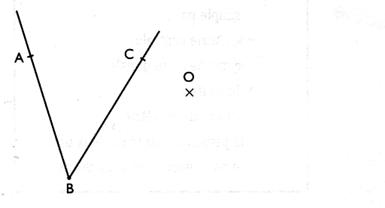
Procédure : On nomme 3 points : le sommet "B" et l'on place un
point " A" et "C"
sur chaque demi - droite . (pour former
l'angle -
Construire le point "A
' " avec la règle et le compas ; tel que le point "O" soit le
milieu du segment A A '. -
Construire le point "B '
" avec la règle et le
compas ; tel que le point
"O" soit le milieu du segment B B '. -
Tracer le segment A'B' . -
Construire le point "C '
" avec la règle et le
compas ; tel que le point
"O" soit le milieu du segment C C '. - tracer le segment B'C' · On
dira que : le segment [B' A'
] est appelé le symétrique du
segment [A B ] , On dira que : le
segment [B' C' ] est appelé le symétrique du segment [BC ] . Les deux segments
[B' A' ] et [B' C' ] ont un point commun B' , ils forment
l'angle ·Vérification : Il faut vérifier , à
l'aide du compas , que les angles Vérification de l' égalité des deux angles
trois solutions immédiates sont possibles : j soit par
mesure à l’aide du rapporteur . k soit par
comparaison à l’aide d’un transparent
ou calque : lsoit par
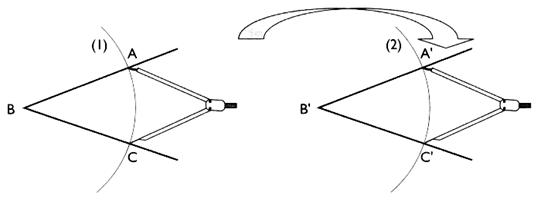
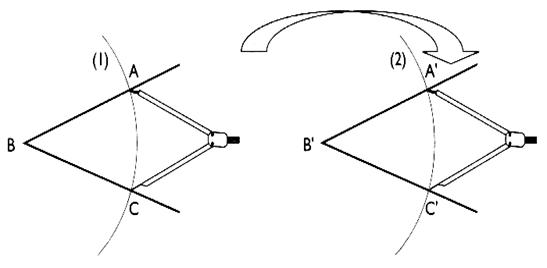
comparaison avec un compas. — Rappel
de la méthode du compas : On trace
les arcs de cercle ( 1) et ( 2) de centre B et B' respectivement de même
rayon .
On règle
l'ouverture du compas AC ; en conservant
la même ouverture , on déplace le compas sur A'C' . Si AC = A'C' , les deux angles ont la même
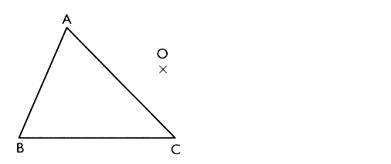
mesure. 4° ) Savoir construire le symétrique du polygone
à trois côtés ( triangle) par
rapport à un point "O".(
voir Cd)
la procédure utilisée pour construire la
symétrie de l’angle est la même que celle qu’il faut mettre en œuvre pour le
triangle : Il faut faire la symétrie de chaque point (sommet) et joindre
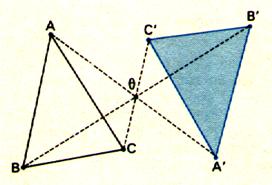
à la règle ces points . Application : On construit les points A' ; B' et C'
symétriques de A ; B et C par rapport
à "O" et l ’ on trace le
triangle A' B'C'
—On dit aussi que l’on fait le symétrique de
chaque segment , qui compose la figure . Activité : tracer
le triangle A ‘ B ‘ C ‘ en
symétrie centrale par rapport au point
O .
N ! On vérifiera à l'aide du compas que les longueurs et les mesures des angles sont conservées dans la
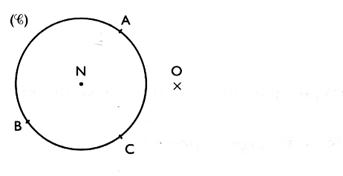
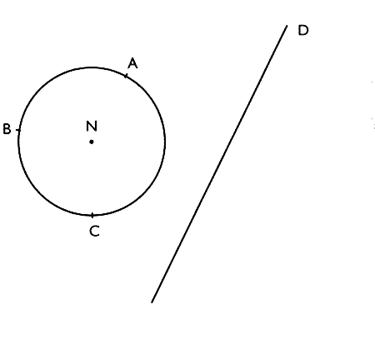
symétrie . 5° ) Construire le symétrique du cercle par rapport à "O" ( voir CD )
Procédure : Construire les points A' , B' C' et N' ,
symétriques de A,B,C et N respectivement par rapport à "O" . Tracer
le cercle ( C ) de centre N' et de rayon N'A' . On peut
constater que ce cercle passe aussi par les points B' et C' .
On peut ajouter d’autres points ! Pour construire le symétrique d'un cercle il suffit de
construire le symétrique du centre et celui d'un point quelconque du
cercle par rapport à zéro . Alors avec
un compas on trace le cercle symétrique de rayon R
= R ’ = OA = OB ; …… Après avoir observé les tracés précédents
: On retiendra : |
|
||||||||||||
|
|
|
||||||||||||
|
Par
une symétrie centrale de centre
"O" : -
l'image d'un
segment est un segment parallèle et de
même longueur . -
l'image d'un
angle est un angle de même mesure . -
l'image d'un polygone est un polygone de mêmes
dimensions. -
L'image d'un
cercle est une cercle de même rayon . La symétrie centrale conserve les longueurs et
les angles . |
||||||||||||||
|
|
||||||||||||||
|
|
|||||||||||||
|
Définition : |
||||||||||||||
|
Quels que soient la droite D et le
point A ,non situé sur « D » , il existe
dans le plan défini par « A » et « D » une droite D et une seule contenant le point « A » et elle est dite « orthogonale » à la droite
« D » . |
|
|||||||||||||
|
Remarque :
Deux droites orthogonales coplanaires
( dans un même plan
) sont dites perpendiculaires. |
||||||||||||||
|
|
|
|||||||||||||
|
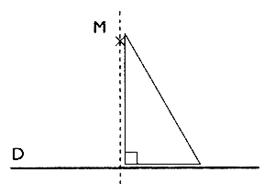
Par M
, on trace une perpendiculaire à D
avec une équerre . |
Si M ’ est la projection orthogonale de M alors la droite passant par MM’ est
perpendiculaire à la droite D |
|||||||||||||
|
IV ) ) TRACES des
éléments de base en SYMETRIE ORTHOGONALE |
||||||||||||||
|
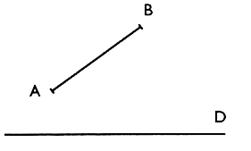
1 ° ) Savoir construire la symétrie orthogonale d’un
point : activité : Placer
un point "A" à une distance de 3,5 cm de la droite ( D) et Construire le
symétrique orthogonal "A' "
par rapport à ( D ) . Procédure : -
Tracer
une demi droite perpendiculaire
à D
, placer le point A. -
Prolonger la demi droite et placer au compas le
points A’ , symétrique de A , tel que O soit le milieu du segment [ A A’ ]. |
||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
De ce côté de « D » placer sur la demi droite le point A à 3,5 cm de D |
De ce côté placer le point A’ |
||||||||||||||||||||||||||
|
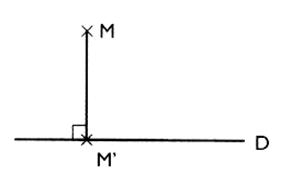
deux
points A et A' sont symétriques par
rapport à la droite ( D ) lorsque la droite ( D ) est médiatrice
du segment [ A A '] La
droite ( D) est l'axe de symétrie , le point A' est l'image de A
dans la symétrie orthogonale d ' axe
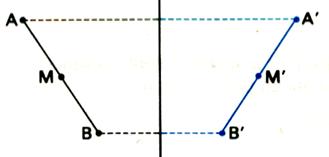
( D ) . 2° ) Savoir construire
le symétrique du segment AB par rapport
à la droite ( D ) . 2 - 1 le segment n’est
pas sécant à l’axe :
-
Construire A' ,
symétrique de A par rapport
à ( D ) : Tracer une droite (d ) perpendiculaire à ( D ) passant par A ,
relever la distance de A à la droite
(D) avec un compas , reporter cette distance sur la droite (D) ( de l'autre côté
de D ) le point A' obtenu est le symétrique orthogonale de A
par rapport à ( D) . -
Construire B' , symétrique de B par rapport à ( D ) : Tracer
une droite (d ) perpendiculaire à ( D
) passant par B , relever la distance de
B à la droite (D) avec un compas , reporter cette distance sur la droite (D)
( de l'autre côté de D ) le point B ' obtenu est le symétrique
orthogonale de B par rapport à ( D) . -
Joindre les deux points A'B' :
Le segment
A'B' est le symétrique du segment AB par rapport à ( D ) . Activité : Construire
le symétrique A’ B’ du segment
A B .
A _ : la symétrie de la droite ( A B ) par , droite portant le segment AB , est la droite ( A ' B ' ) , droite
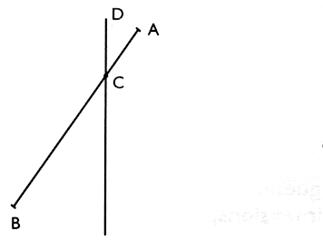
portant le segment A' B ' . 2 - 2 ) le segment coupe
l’axe : Construire A' symétrique de A par rapport à ( D ) puis B' , symétrique de "B"
par rapport à ( D ) . Le segment
A'B' est le symétrique du segment AB
par rapport à ( D).
— On remarque que le symétrique de C
; C' sont superposés . N ! On vérifiera que les longueurs A'B' et AB sont égales
et que les segments A'B' et A B se
correspondent par pliage suivant la droite ( D ) .
D D ’ 2 - 3 ) le segment
( D ) est perpendiculaire à l’axe delta ( D ) : Procédure : on
détermine des bornes ( 2 points nommés
) et l’on trace la symétrie orthogonale de chaque point ; on trace ,pour
conclure, une droite passant ces bornes symétriques.
. — On
remarque que le symétrique de C ; C' sont superposés . N ! On vérifiera que la perpendicularité est conservée . 3° )Savoir Construire
le symétrique de deux droites sécantes
(angle ) par rapport à la
droite ( D )
( Info :voir / O) — exemple :
l’angle
— Activité : tracer l’angle Cela
revient à construire [ A' B'] et [ B'
C'] , symétriques de [AB] et [BC] par
rapport à ( D)
On
comparera, à l'aide d'un compas, les angles. N ! Il faut vérifier , à l'aide du compas ,
que les angles Vérification de l' égalité des deux angles trois solutions immédiates sont
possibles : j soit par
mesure à l’aide du rapporteur . k soit par
comparaison à l’aide d’un transparent
ou calque : lsoit par
comparaison avec un compas. — Rappel
de la méthode du compas : On trace
les arcs de cercle ( 1) et ( 2) de centre B et B' respectivement de même
rayon . On règle l'ouverture du compas AC ; en conservant la même ouverture , on déplace le compas
sur A'C' . Si AC = A'C' , les deux
angles ont la même mesure. —
Si le tracé
est effectué sur un transparent ( ou calque) , on peut aussi faire la vérification par
pliage suivant la droite ( D ) , les
figures se superposent . 4°)Savoir construire le
symétrique de deux droites
parallèles par rapport à la
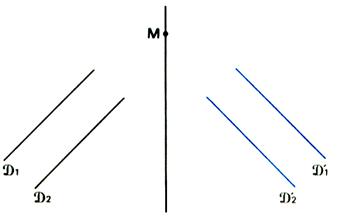
droite ( D ) nous avons vu que A _ :
« la symétrie d ’ une
droite ( D ) , droite portant un
segment [ ], est la droite ( D ' ) , droite
portant un segment [ ’ ’ ]’ . Ce qui est vrai pour une droite est vrai pour une deuxième droite , quelque
soit la position entre ces deux droites . Procédure : On
tracera deux points appartenant à chaque droite , pour obtenir deux segments . On fera ensuite , la
symétrie orthogonale des bornes de
chaque segment . Il n’y aura plus qu’a tracer les deux droites passant par ces bornes
.(on vérifiera que
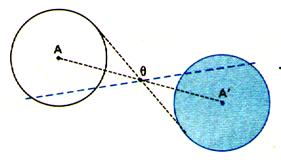
le parallélisme est conservé) « SYMETRIQUES ORTHOGONALES DE FIGURES. » 5° ) Savoir construire
le symétrique du cercle par
rapport à la droite ( D ) — exemple :
On
construit le symétrique du centre et celui du point du cercle par rapport à
la droite ( D ). Construire
les points A’ , B’ , C’ et N’ ,
respectivement symétriques de A , B ,
C et N par rapport à la droite ( D). Construire
le cercle de centre N’ et de rayon N’
A’ . On constatera que
le cercle passe aussi par les
points B’ et C’ . 6° ) Savoir construire
le symétrique orthogonal d ’ une ligne courbe — pour faire la symétrie d’une
ligne courbe , il faudra rechercher le centre de chaque arc de cercle s’il existe , autrement il faudra faire la symétrie
d’un très grand nombre de points
rapprochés et choisis sur cette courbe . exemple : vu au
début du cours
7 °) Savoir construire
le symétrique du « polygone » par rapport
à la droite ( D ) . Rappel
de la définition d’un polygone : Un polygone est une portion de
plan limitée par une ligne brisée fermée. —Les polygones usuels sont le triangle , le
rectangle , le carré , le trapèze , le losange . — Procédure
à utiliser pour effectuer la
symétrie orthogonale d’un polygone : -
Nommer
chaque extrémité de segment ( toutes)
ou ( tous les sommets d’angle) , et centre d’arc de cercle (s’il
existe) par une lettre différente .(pour ce marquage il est conseillé de tourner
toujours dans le même sens , par exemple le sens des aiguilles d ‘ une montre
) -
Construire le symétrique de tous les points . -
Joindre
chaque point par une ligne droite ou
courbe , suivant le cas. Attention
de bien suivre l’ordre des
points ! ! ! ! En procédant ainsi on a construit le symétrique de chaque côté de
la figure par rapport à la droite ( D
). 7 -
1 le polygone est un triangle . Activité : construire le symétrique orthogonal du triangle ABC par rapport à la droite D .
Procédure :
Construire les points A’ , B’ et C ‘
, respectivement symétriques de A ; B et C par rapport
à la droite ( D). Joindre
les points A ‘ , B’ et C’ . N !On
vérifiera , à l’aide d’un compas , que
les longueurs des côtés et les mesures des angles sont conservées
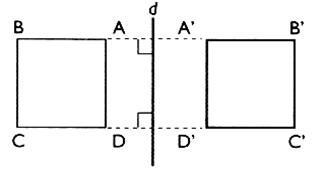
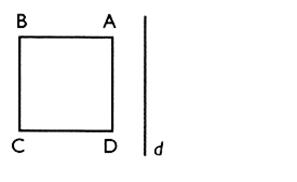
dans la symétrie . 7 - 2 le
polygone est un carré : Procédure : On construit les points A ' B'
C' et D' , respectivement symétriques de A , B , C et D .et l'on joint les points .
· L’ordre des tracés des points n’est
pas important , mais il faut prendre garde
de ne pas joindre B’ et D
’ ainsi que C’ et A’ Activité : construire le symétrique du polygone par rapport
à une droite ou axe .( d )
7 - 3 le polygone est un rectangle : Procédure : On construit les points A '
B' C' et D' , respectivement
symétriques de A , B , C et D .et l'on
joint les points .
L’ordre des tracés des points n’est pas important , mais il faut prendre
garde de ne pas joindre B’ et D’
ainsi que C’ et A’ 8
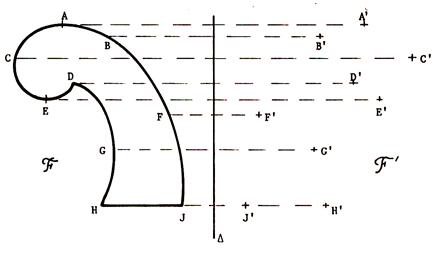
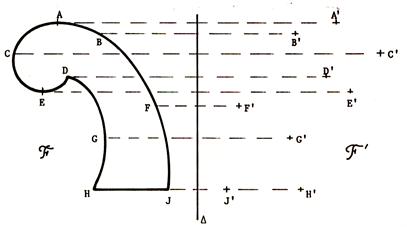
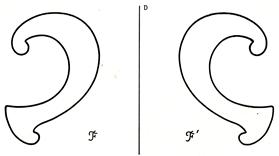
°)Savoir construire ( tracer ) une figure quelconque : Exemple : ci
dessous F’ est
la symétrie orthogonale de la figure F
par rapport à une droite « delta » . Remarquez que le
choix des points sur F doit être
réfléchi .
· L’image de « F » dans
la symétrie orthogonale par rapport a « delta » est une figure
« F’ » constituée par l’ensemble des points qui sont les
symétriques des points de « F ». · Sur le dessin ci-dessus , on a choisi quelques
points de « F » et on a déterminé leurs images .En imaginant que l’on fait la même chose pour
tous les points de « F » ,on peut compléter la figure
« F’ » .
REMARQUES : · Dans une symétrie orthogonale chaque point « une Figure » et « son image » sont superposables ( par pliage) . Ce qui signifie
que dans une symétrie orthogonale la figure et son image ont donc même forme
et mêmes dimensions. i Ce constat étant
fait , la leçon suivante portera sur
les propriétés de la symétrie
centrale et sur les propriétés de la
symétrie orthogonale . |
|||||||||||||||||||||||||||