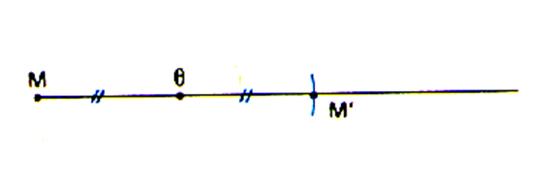|
|
Pré requis:
|
|
|
|
Le point |
|
|
Symétrie centrale
1 |
ENVIRONNEMENT du
dossier:
|
Objectif
précédent : |
Objectif
suivant : |
2°)liste des objectifs cours de géométrie plane. |
DOSSIER : SYMETRIE CENTRALE N°2
1.
Définition d'une
symétrie centrale
2.
PROPRIETES d'une
SYMETRIE CENTRALE
3.
Symétrie centrale de figures
simples:
4.
Résumé
|
TEST |
COURS |
Interdisciplinarité |
|
(dans « centrale » il y a
« centre », le « centre » est assimilable à un
« point » )
Deux points possèdent un centre de symétrie (voir médiatrice d’un segment)
Définition d'une
symétrie centrale:
Soit
un point O donné ; on appellera "symétrie centrale" de centre O , noté "So
" l' application du plan R dans
le plan R (noté : R ® R) qui
associe à tout point M le point M' (on dit aussi :que le point M a pour image le
point M' ) tel que "O" soit le milieu du segment MM' noté [ MM']
Ce qui se traduit en écriture mathématique:
So : R ® R
M
![]() M' , O = milieu [ MM']
M' , O = milieu [ MM']
Construction
de l'image d'un point :
|
L'image du point ( M') se trouve sur la droite passant par les points
MO et à l'intersection de cette
droite avec l'arc de cercle de centre
O et de rayon MO . |
|
PROPRIETES d'une
SYMETRIE CENTRALE:
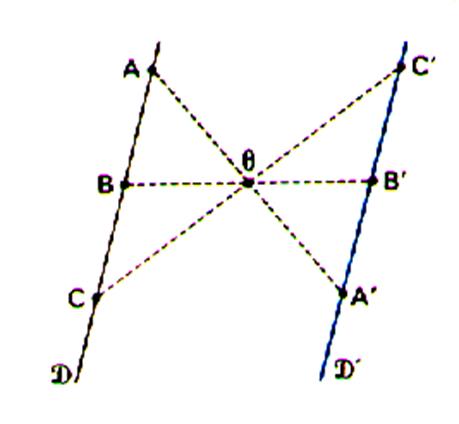
L'image d'une droite D est une
droite D' , telles que les droites sont
parallèles ( Pour ce qui est d'un
vecteur : cela est vrai pour la direction mais pas pour le sens )
|
On dit que la symétrie centrale conserve l'alignement. |
|
|
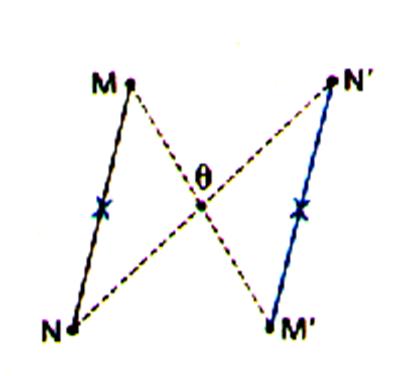
Une
symétrie conserve les distances . d( M,N) = d(M' ,
N' ) |
|
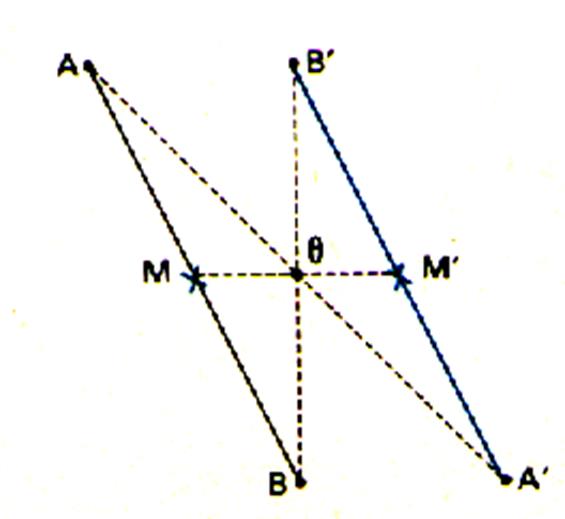
L'image du milieu d'un segment est le milieu du "segment - image"
|
|
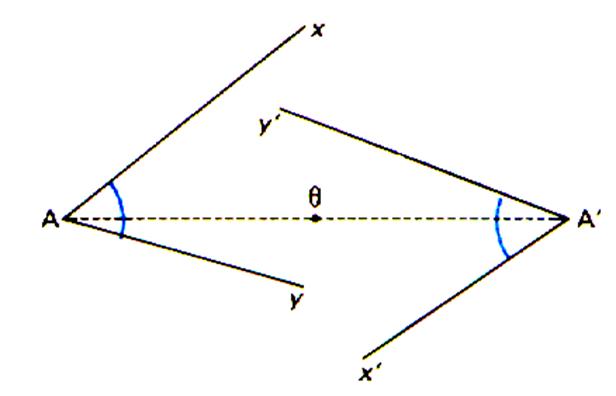
Une symétrie centrale conserve les angles:
|
|
Symétrie
centrale de figures simples:
|
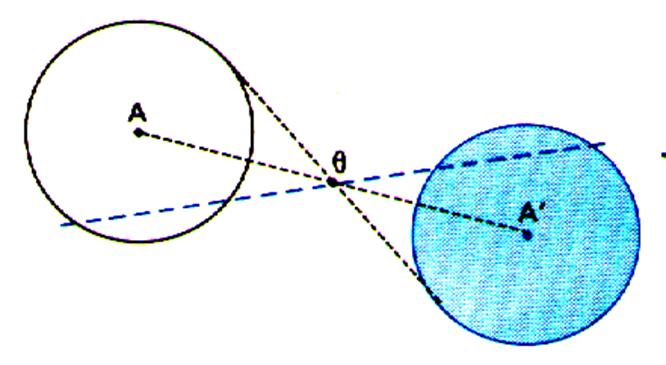
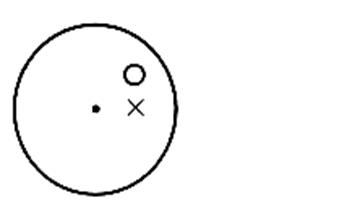
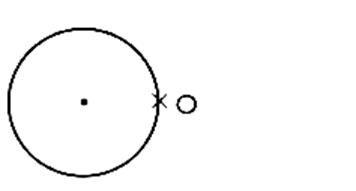
L'image
d'un cercle est un cercle de même
rayon. Donc
: l'image d'un disque est un disque de même aire. |
|
|
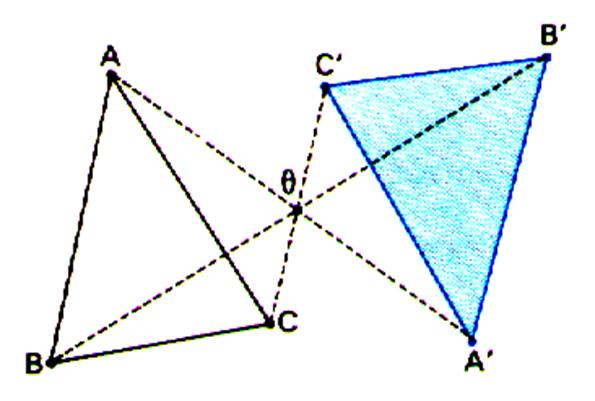
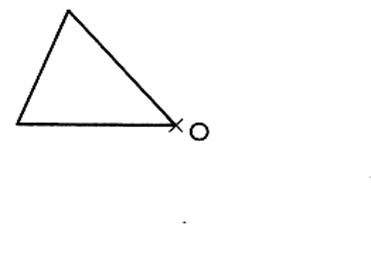
L'image d'un triangle est un triangle de mêmes dimensions |
|
|
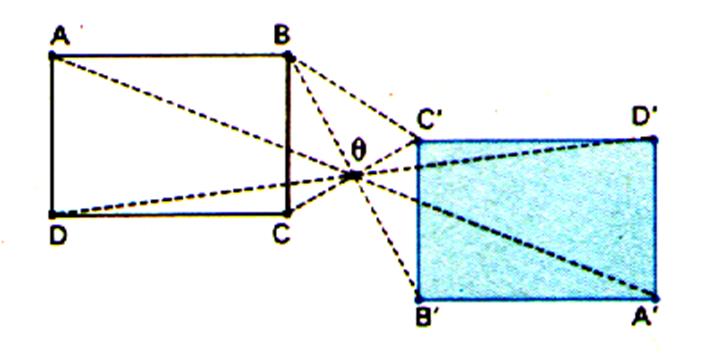
L'image d'un rectangle est un rectangle de mêmes dimensions |
|
Ainsi : L'image d'un carré
est un carré de mêmes dimensions et
L'image
d'une figure quelconque est une figure quelconque de mêmes dimensions
PROPRIETES : EN
CONCLUSION
( INFO :à retenir 5e : à relier avec celles du parallélogramme
)
|
Une
symétrie centrale conserve : L'alignement Les longueurs Les angles Il en résulte que toutes figures
géométriques à pour image une figure de même dimension
, donc de même aire. Une
symétrie centrale conserve aussi : les aires . |
TRAVAUX AUTO FORMATIFS.
Que conserve une symétrie centrale ?
Traduire en écriture littérale :
So : R ® R
M ![]() M' , O = milieu [ MM']
M' , O = milieu [ MM']
Corrigé: on appelle "symétrie centrale" de centre O , noté "So
" l' application du plan R dans le plan R (noté : R ® R) qui associe à
tout point M le point M' tel que "O" soit le milieu du segment MM'
noté [ MM']
1°) dessiner un segment AB de
Construire le symétrique [A ' B '] du segment AB par rapport à
"O" .
Vérifier que le symétrique du milieu "I"
du segment AB ; "I'" est milieu du segment A' B' .
On dit que la symétrie centrale conserve le milieu
.
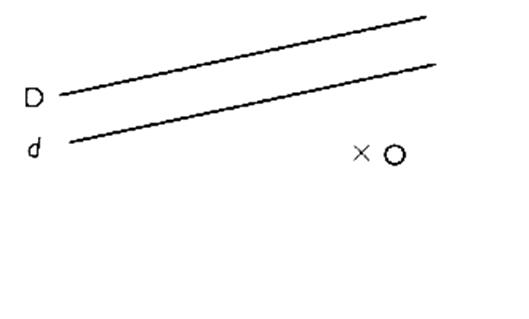
2°) Construire le symétrique des deux droites
parallèles ( D ) et ( d ) par rapport à
"O" .
Vérifier si les images D' et d' sont parallèles .
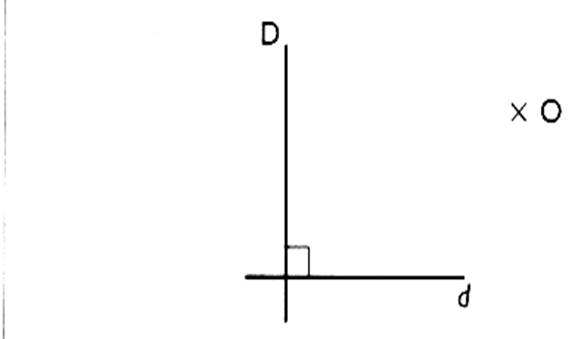
3° ) Construire le symétrique des deux droites
perpendiculaires ( D ) et ( d) par
rapport à "O" .
Vérifier que les images ( D' ) et ( d' ) sont perpendiculaires .
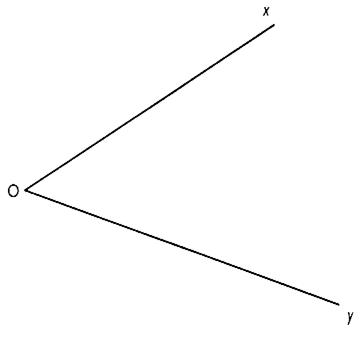
4°) construire le symétrique de l'angle par rapport
à "O"
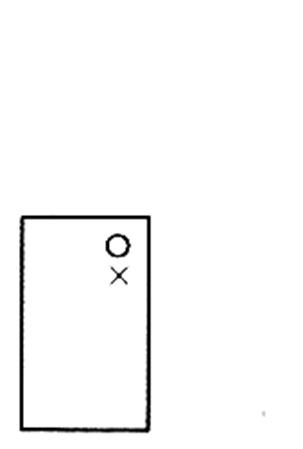
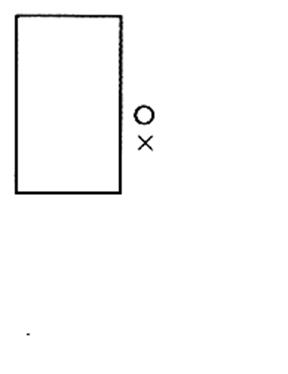
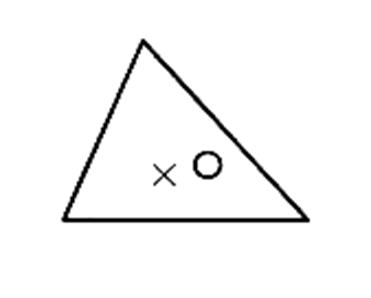
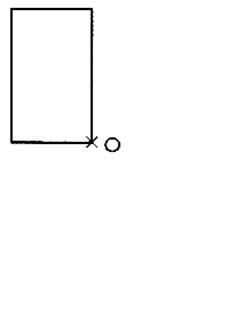
5°)Construire les symétriques des figures ci -
dessous par rapport au point "O"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|