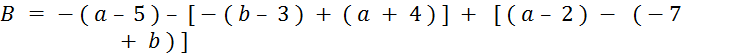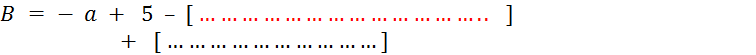|
Juin 2014 |
|
Niveau :
Classe de collège : 4ème |
|
|
|
|
|
|
||
|
Objectifs les
égalités : vocabulaire 1EG1 |
|
|
|
égalités les
égalités : vocabulaire 2 EG2 |
|
|
ENVIRONNEMENT du dossier :
|
Objectif précédent : |
.
|
|
DOSSIER : LES SOMMES ALGEBRIQUES |
|
|
|
Fiche 1
–Simplification de l’écriture d’une somme ou d’une différence de deux nombres . |
|
|
|
Fiche 2 -Calcul d’une somme de deux nombres (relatifs)
écrite sous forme simplifiée. |
|
|
|
Fiche 3 : Les sommes algébriques. |
|
|
|
Fiche 4 : Nouvelle écriture de l’opposé d‘un
nombre relatif. |
|
|
|
Fiche 5 : Des lettres dans une somme
algébrique. |
|
|
|
Fiche 6 : Des parenthèses dans une somme
algébrique. |
|
|
|
Fiche 7 : (après
les parenthèses) Cas des crochets . |
|
|
|
Fiche 8 : Exemples d’utilisation des nombres
relatifs et des sommes algébriques :les
moyennes . |
|
|
|
Fiche complémentaire : Calcul des coordonnées
du milieu d’un segment. |
|
|
|
|
|
|
COURS |
Interdisciplinarité |
|
|
|
Fiche 1
–Simplification de l’écriture d’une somme ou d’une différence de deux nombres . |
|
||||||||||||||
|
|
(Faîtes bien attention, savoir simplifier
c’est savoir remettre sous la forme non-simplifiée) |
|
||||||||||||||
|
|
|
|
||||||||||||||
|
|
Vous savez que, par exemple, le nombre relatif ( + 27) peut s’écrire « 27 »
et que dans certaines circonstances , ( - 43 ) peut
s’écrire « - 43 » |
|
||||||||||||||
|
|
En utilisant le fait que
« a – b = a + Opp. b ou que « a + b = a – Opp. b , vous avez vu en classe de « 5ème » comment simplifier l’écriture
d’une somme ou d’une différence. ( mais , attention, savoir simplifier c’est
aussi savoir ré- écrire la forme non-simplifier , sinon vous risquez de
commettre des erreurs ….° |
|
||||||||||||||
|
|
Ainsi : |
|
||||||||||||||
|
|
( +3 ) + ( + 7) |
s’écrit 3 + 7 |
De même. |
( - 13 ) + ( + 2 7) |
s’écrit : |
|
||||||||||
|
( +9 ) + ( - 7) |
s’écrit 9 - 7 |
De même. |
( -39 ) + ( - 67) |
s’écrit
|
||||||||||||
|
( +5 ) - ( + 9) |
s’écrit 5
- 9 |
De même. |
( - 69 ) -
( -
17) |
s’écrit |
||||||||||||
|
( + 6 ) - ( - 3) |
s’écrit 6
+ 3 |
De même. |
(- 28
) - ( - 87) |
s’écrit
|
||||||||||||
|
|
|
|
||||||||||||||
|
|
Activités n°. : Simplifiez de même l’écriture des
sommes suivantes . ( Ne
pas effectuer le calcul ) ; |
|
||||||||||||||
|
|
( -26 ) + (-
78 ) = |
|
|
(+ 36 ) - ( - 93 ) = |
|
|
(+85 ) -
(+ 43 ) = |
|
|
|||||||
|
( -13 ) - (+ 55 ) = |
|
|
(+57 ) + ( -23 ) = |
|
|
( - 73 ) - ( - 47 ) = |
|
|||||||||
|
( |
|
|
( |
|
|
( |
|
|||||||||
|
|
|
|
||||||||||||||
|
|
( mais , attention, savoir simplifier c’est
aussi savoir ré- écrire la forme non-simplifier , sinon vous risquez de
commettre des erreurs ….° |
|
||||||||||||||
|
|
Activités n° .. : Transformer les écritures simplifiées en écriture
dite « algébrique »… |
|
||||||||||||||
|
|
|
|
||||||||||||||
|
|
-26 – 78 = |
|
|
36 +93 = |
|
|
85 - 43 |
|
|
|||||||
|
-13 – 55= |
|
|
57
– 23 = |
|
|
-
73 + 47 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||
|
|
Fiche 2 - Calcul d’une somme de deux nombres
(relatifs) écrite sous forme simplifiée. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Cas 1 : Les nombres sont séparés par le signe « + ». |
|
|||||||||||||
|
|
Opération : |
Commentaire : |
C’était l’écriture
algébrique….. |
Calcul : |
|
||||||||||
|
|
25 + 43 |
Ce calcul ne présente aucune difficulté …. |
( + 25 ) + ( + 43 ) = |
25
+ 43 =
…….. |
|
||||||||||
|
-15 + 52
|
C’est la somme de
…. Et de ……. |
( - 15 ) + ( + 52 ) = ( + (52-15))= ( + 37) |
-15 + 52
= ………………………. |
||||||||||||
|
-76 + 39 |
C’est la somme de
….
Et de ……. |
( -76) + ( +38) = (
- ( 76 – 39 ) ) = ( - 37) |
-76 + 39
= ……………………………. |
||||||||||||
|
|
Dans les calculs (1) et (2) nous sommes en
présence de la somme
de deux nombres relatifs ( @) de signe contraire. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Cas 2 : Les nombres sont séparés par le signe « - ». |
|
|||||||||||||
|
|
Opération : |
Commentaire : |
C’était l’écriture
algébrique….. |
Calcul : |
|
||||||||||
|
|
31 – 86 |
C’est la somme de
….
Et de ……. |
( +31) + ( - 86) = ( - ( 86 – 31) ) = ( - 55 ) |
31 – 86 =……….
|
|
||||||||||
|
75 – 32 |
C’est la somme de
…. Et de ……. |
( + 75 ) + ( - 32 ) = ( + ( 75 – 32) ) = ( + 43 ) |
75 – 32 = …….. |
||||||||||||
|
-18 - 43 |
C’est la somme de …. Et de ……. |
( - 18 ) + ( - 43 ) = ( - ( 18 + 43 )) = ( - 61) |
-18 – 43 = ……….. |
||||||||||||
|
-65 - 27 |
C’est la somme de
….
Et de ……. |
( - 65 ) + ( - 27) = ( - ( 65 + 27) ) = ( - 92) |
-65 – 27 = ………… |
||||||||||||
|
|
|
|
|||||||||||||
|
|
Vous constatez que dans tous les cas , on est ramené à une « addition ». Tout se passe comme si l’on avait sous – entendu
un signe « + » (plus) entre les deux nombres . Ainsi
« -74 +35 » n’est
autre que « ( - 74) + ( + 35)
.l’écriture « -18 – 43 » n’est autre que l’écriture « ( - 18) + ( - 43) ». Vocabulaire : On pourra donc parler de
« somme » même s’il y a un signe « - » (moins) entre les deux nombres. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Méthode pratique de
calcul d’une somme de deux nombres dits « relatifs ». |
|
|||||||||||||
|
|
Le calcul
« 75 + 32 » ne pose pas de problème,……..le résultat est le
nombre « ( + 107) » Il reste 5 types de difficulté : |
|
|||||||||||||
|
|
Difficulté n°1 |
Difficulté n°2 |
Difficulté n°3 |
Difficulté n°4 |
|
||||||||||
|
75 – 32 |
-15 + 53 |
33 - 87 |
-19 - 47 |
||||||||||||
|
|
Puisque
75 > 32 , vous pouvez faire la
soustraction |
Dans ce cas et en considérant que
l’opération est une addition et comme l’addition est commutative
, alors « -15 + 52 = 52 –
15 », on est ramené à la difficulté 1 . |
Dans ce cas , vous
savez que l’opposé de « 33-87 » est « 87-33 », or
« 87-33 » se calcule facilement , « 87 – 33 = …… » donc « 33-87= ….. » |
De même |
|
||||||||||
|
|
|
|
|||||||||||||
|
|
Pour découvrir un
début de solution il faut transformer
les écritures précédentes en
écritures algébriques…….. |
|
|||||||||||||
|
|
( +75) + ( – 32) |
( -15) + ( + 53) |
( +33) + ( - 87) |
(-19) + (- 47) |
|
||||||||||
|
|
|
|
|||||||||||||
|
|
Difficulté n°5 :
- 76 + 43 |
De même l’opposé de « -76 + 43 » est
« 76 – 43 ». Or : 76 – 43 = 33 , donc - 76 + 43 = - 33 |
Remarque : : - 76 + 43 s’écrit
sous la forme d’une somme algébrique : « ( -76) + ( + 43) » |
|
|||||||||||
|
|
|
|
|||||||||||||
|
|
Nota : pour réussir tous ces calculs
il faudrait travailler les
objectifs de formations proposés ici @ …. |
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Activité :n°1…(sur copie) |
|
|||||||||||||
|
|
Faire les exercices proposés : 1°) En passant par les « opposés »
quand cela est nécessaire. 2°) En passant par la transformation en
somme algébrique. |
|
|||||||||||||
|
|
24 – 36 = ………….. |
- 43
– 37 = ……………. |
-79 + 26 = ………. |
-61
+ 61 = ………. |
|
||||||||||
|
56 + 27 = …………… |
59 – 33
= ……………. |
-15 – 67 = …………. |
- 37 + 97 = ……….. |
||||||||||||
|
|
|
|
|
||||||||||||
|
Activité :n°2…(sur copie) |
Calculez , comme ci –dessus… |
|
|
||||||||||||
|
8 + 2 = …………. |
8 – 2 = ……………. |
-8 +
2 = …………. |
-8 – 2 = ………….. |
||||||||||||
|
2 +
8 = ………….. |
2 – 8
= …………… |
-2 + 8 = ……………. |
-2
- 8 = …………. |
||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
||||
|
|
Fiche 3 :
Les sommes algébriques. |
|
|||||
|
|
|
|
|||||
|
|
Aux fiches 1 et 2
, on a simplifié et
calculé des sommes de deux termes. Il est possible de faire de même pour des
sommes de plusieurs termes. Ainsi : A = ( +8 ) + ( - 5 ) + ( - 7 ) + ( + 6
) s’écrit : A =
8 – 5 ………………… De même
B = ( + 9 ) – ( - 3 ) + ( - 8 )
– ( + 7 ) s’écrit B = 9 + 3 …………..
A = 8 – 5
- 7 + 6 et B = 9 + 3 – 8 – 7 sont appelées des expressions algébriques (mais on les appelle couramment aussi : « sommes algébriques ») |
|
|||||
|
|
·
Vous pouvez calculer
« A » et « B » comme dans la fiche 2 ( en faisant les
calculs de gauche à droite). |
|
|||||
|
|
|
A = ………. - 7 + 6
|
|
B =
……. – 8
– 7 |
|
|
|
|
|
= …… - 7
+ 6 |
|
= … -
8 - 7 |
|
|||
|
|
= - 4 + 6 |
|
= 4 -
7 |
|
|||
|
|
= + 2 |
A = 2 |
= - 3 |
B =
- 3 |
|||
|
|
|
|
|||||
|
|
Activités N° ..: Donnez l’écriture simplifiée de
« C » et « D » puis calculez les sommes simplifiées
(comme précédemment ) |
|
|||||
|
|
C = ( + 6 ) + ( - 8 ) – ( - 9 )+ ( + 4 )- (
+7 ) + ( - 1 ) = …………………………… = |
|
|||||
|
|
D =
( - 0 ,9 ) + ( 2 , 4 ) – ( - 5,3 ) – ( + 3 , 5 ) =
…………………………………. = |
|
|||||
|
|
|
|
|||||
|
|
Ci-dessous avec des nombres entiers |
Ci-dessous avec des nombres décimaux. |
|
||||
|
|
E = 9 – 5 + 4 – 8 + 6 – 7 = ……… |
G = - 4,3 – 7,3 + 8,5 – 2,3 + 3,7 =………. |
|
||||
|
F = - 4
- 5 + 9 – 7 + 8 – 2 = ……………… |
H = 3,9
- 2,1 + 0,6 – 4,5 + 5,2 =……….. |
||||||
|
|
|
|
|||||
|
|
A ) Autre méthode de calcul d’une somme
algébrique. |
|
|||||
|
|
Une somme algébrique pouvant être
considérée comme une succession d’additions et l’addition étant commutative, on peut alors changer l’ordre des termes. Ainsi : C =
5 – 8 + 9 + 4 – 7 – 1 peut
s’écrire C = -8 + 4 – 7 + 5 – 1 + 9 ou
C = …………………………….. ·
De plus , l’addition étant associative , il
est possible de regrouper d’une part les termes précédés du signe
« + » et d’autre part, les
termes précédés du signe « - » Ainsi : C =
( 9 + 5 + 4 ) + ( - 8 – 7 – 1 ) , poursuivez le calcul : C
= ( ….. ) + ( ……. ) = ……… ·
Le regroupement peut se faire mentalement . On écrira alors directement :
J =
44 – 27 + 12 – 37 – 49 + 17
= ( ……)
+ ( ……) = ………. K = 44,3
– 27,5 + 12 ,6 – 37,3 – 4,9 + 1 , 7 = (
……) + ( ……) = ………. |
|
|||||
|
|
B ) Simplification des opposés. |
|
|
||||
|
|
On fait comme nous l’avons vu , dans la leçon 5 « Fiche
3 »,
on surligne les opposés. |
|
|||||
|
|
Ainsi : M = 9 + 2 -4 – 8 + 7
+ 4 – 6 + 8 - 9 = ………………………. = ……………. ·
Faites de même pour N =
2,5 + 5 ,
1 – 8,2 + 4 , 7 – 5,1 – 6, 3 + 8,2
= ………….. ·
On va voir aussi que l’on peut regrouper plusieurs termes : « - 5 – 2 » se simplifie avec
« +7 » Ainsi calculez : P = 5
– 9 + 3 – 7 + 4 +2 – 8 + 6 = ………… R = - 6,8
- 2,9 + 3,5 + 5 , 7 - 1,2 + 4,1- 7 , 6 + 2,3 = ……. |
|
|||||
|
|
|
|
||||||
|
|
Fiche 4 : Nouvelle
écriture de l’opposé d‘un nombre relatif. |
|
|
|||||
|
|
On désigne par la lettre « a » un
nombre relatif quelconque , vous savez que « …….. » s’écrit
« ……. » et
« …….. » s’écrit
« ……… » C'est-à-dire que
« - ( +
5) = - 5 » et « - ( - 7 ) = + 7 » Ou encore : - ( + 5 ) = Opp ( + 5 ) et - ( - 7 ) = Opp ( - 7) on peut donc dire : |
|
||||||
|
|
A retenir : Mettre le signe « - »
devant un nombre , revient à écrire « …… …….. » de ce nombre. |
|
||||||
|
|
|
|
||||||
|
|
D’une manière
générale, « a » désignant un nombre relatif, |
« - a = Opp ( a
) » |
|
|||||
|
|
ATTENTION : |
|
||||||
|
|
On vous propose 2 phrases
, l’une est vraie l’autre est fausse , encadrez la réponse vraie ,
barrez la réponse fausse. |
|
||||||
|
|
|
« - a » est toujours négatif |
|
« -a » n’est pas forcément
négatif |
|
|
||
|
|
|
|
||||||
|
|
|
|
|
|
|
Fiche 5 : Des
lettres dans une somme algébrique. |
|
|
|
|
|
|
|
|
|
Dans une somme algébrique dans laquelle
figurent des lettres « a » , « b » , « c » ». Ces lettres représentent des nombres
relatifs. Exemple : R =
7 + a + 5 – b – c + 3 – a - 8 +
b Bien qu’il y a des lettres précédées du
signe « - » , on peut dire que
« R » est une somme. En effet , «
7 – b » n’est autre que « 7 + Opp (b) c'est-à-dire « 7 + ( - b ) ». Ø Pour calculer « R » , on additionne
les nombres écrits en chiffres ( voir l’exemple dans la fiche 3) et
pour les lettres, on additionne les opposés en remarquant que « a – a = ….. » et « b – b = ……. » Vous
trouvez : R = ……. |
|
|
|
|
Ø Calculez de même : T = V = - n – 9 + 3 – m +
7 + n – 6 + m – n + 2 = ………………………….. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Fiche 6 : Des
parenthèses dans une somme algébrique. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Rappelons la règle étudiée en classe de « 5ème . » . cette règle s’applique
aussi aux lettres. |
|
||||||||||||||||||||||||||||||||||
|
|
A retenir : Dans une somme algébrique contenant des parenthèses,
on peut supprimer ces parenthèses et le signe situé devant
, à condition : -
De ne rien changer si le signe précédant les parenthèses est ………… -
De changer les signes situés à l’intérieur des parenthèses si le
signe situé devant est …« ……….. » …. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Activités n°1….. : En appliquant la règle ci-dessus, supprimez les parenthèses (sans effectuer de calcul). |
|
||||||||||||||||||||||||||||||||||
|
|
9 + ( 6 – 7 + 8 )
= |
|
6 - ( 3 + 7 – 4 )
= |
|
|
|||||||||||||||||||||||||||||||
|
5 + ( - 8 + 2 – 7 ) = |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
2 – ( - 9 – 7 + 6
) = |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Activités n°.2. |
|
||||||||||||||||||||||||||||||||||
|
|
On vous demande de calculer « B » de deux façons
différentes : 1°) Vous effectuez les calculs indiqués
(Vous faîtes d’abord le calcul dans
les parenthèses). 2°) Vous supprimez les parenthèses avant
d’effectuer les calculs. B = ( - 8 + 9 – 2 ) - ( 5 + 4 – 6 ) + ( 2 – 8 ) - ( - 9 + 4 – 7) |
|
||||||||||||||||||||||||||||||||||
|
|
1ère méthode : B = ( …..
) - ( ……
) + ( ……
) - ( …. ) B = ( …..
) + ( ……
) + (…… )
+ ( …..) B = ( …….. ) + ( ….. ) B = ( …..
) |
|
||||||||||||||||||||||||||||||||||
|
|
2ème méthode : B =
……………………………………………….. B = …………………………………………….. B =
……………………… |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Activité N° 3… Faites de même pour : C = - ( - 5 + 2 – 6 ) + ( - 7 + 4 –
5) – ( 2 + 8 – 5 ) + ( 7 – 4 + 9 ) |
|
||||||||||||||||||||||||||||||||||
|
|
1ère méthode : C =
- ( ……. ) + ( …….. ) - (
……. ) + ( ……. ) |
|
||||||||||||||||||||||||||||||||||
|
|
2ème méthode : C = + 5 - 2 + 6 -
7 + 4 – 5 – 2 -
8 + 5 + 7
– 4 + 9 C = …………………………………………………………..…… |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Activité N° 4… Après avoir supprimé les parenthèses
calculez : ( « s » et
« n » représentent des
nombres). D =
( D =
…………………………………………………………………….. D =
Etait-il possible de faire cet exercice par
l’emploi de la première méthode ? ……….…………… Vous comprenez donc l’utilité de la règle
relative à la suppression des parenthèses… |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Activité N° 5…( avec des lettres ) Calculez après avoir enlevé les parenthèses
( les lettres
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Fiche 7 : Cas des crochets. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
La règle de suppression des crochets est la
même que celle des parenthèses. Exemple :
A = ( 8 – 3 + 6 ) + [ ( 7 – 9 – 3 ) - ( 2 + 4 – 8 ) ] -
[ - ( 4 + 8 – 3 ) + ( - 2 + 6 ) ] Méthodes différentes que l’on
vous demande d’ appliquer : 1°) Faîtes les calculs indiqués.(dans chaque
parenthèses, puis ……) 2°) Enlevez les parenthèses puis les
crochets ( sans effectuer les opérations). 3°) Enlevez les crochets puis les
parenthèses ( Sans effectuer les opérations). 4°) Effectuez les calcul du résultat obtenu
au « 2°) » ou au « 3°) » . |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Méthode 1 : Faîtes les calculs indiqués
A = ( 8 – 3 + 6 ) + [ ( 7 – 9 – 3 ) - ( 2 + 4 – 8 ) ] -
[ - ( 4 + 8 – 3 ) + ( - 2 + 6 ) ] A
= ( ….. ) + [
(…… )
- ( …….
) ] - [
( …….. ) + ( …….. ) ] A
= ( ….. ) + [ ( ……. ) + ( …… )
] - [ - 5
] A
= ( …….. ) + ( ……. ) +
( ……. ) A
= ( …….. ) + ( …….. ) + ( ……. ) A = ……… |
|
||||||||||||||||||||||||||||||||||
|
|
Méthode 2 : Enlevez les parenthèses
puis les crochets ( sans effectuer les opérations).
A = ( 8 – 3 + 6 ) + [ ( 7 – 9
– 3 ) - ( 2 + 4 – 8 ) ] -
[ - ( 4 + 8 – 3 ) + ( - 2 + 6 ) ] A = (
8 – 3 + 6 ) + [ ( 7 – 9 – 3 ) - ( 2 +
4 – 8 ) ] - [
- ( 4 + 8 – 3 ) + ( - 2 + 6 ) ] A = ( 8 – 3 + 6 ) + [ …………………………….. ]
- [ …………………………….. ] A = ( 8 – 3 + 6 ) …………………………………………………………………………… A
= ( 11
) + 7 – 9 – 3 - 2
- 4 + 8 …………………………….. A = 11 – 3 +
5 = 16 – 3 = 13 |
|
||||||||||||||||||||||||||||||||||
|
|
Méthode 3: Enlevez les crochets puis les
parenthèses ( Sans effectuer les opérations). A
= ( 8 – 3 + 6 ) + [ ( 7 – 9 –
3 ) - ( 2 + 4 – 8 ) ] -
[ - ( 4 + 8 – 3 ) + ( - 2 + 6 ) ] A
= ( 8
– 3 + 6 ) + ………………………………………………………………………….. A
= ( 8 – 3 + 6 ) + ……………………………………………………………………………… Si l’on compare cette dernière ligne avec
la dernière ligne « 2°) » on retrouve les mêmes valeurs
numériques…. 4°) Fin du calcul : A
= …………………………………………………………………………. = ……………………… |
|
||||||||||||||||||||||||||||||||||
|
|
Activité n° .1. |
|
||||||||||||||||||||||||||||||||||
|
|
Faites de même pour |
|
||||||||||||||||||||||||||||||||||
|
|
C = [ ( 9 – 5 + 2 ) - ( - 7 + 4 + 6 ] - [
- ( 9 – 3 – 4 ) + ( - 4 – 9 + 5 ) ] |
|
||||||||||||||||||||||||||||||||||
|
|
1°)
Calculs indiqués : C = [ ( 9 – 5 + 2 ) - ( - 7 + 4 + 6) ] - [
- ( 9 – 3 – 4 ) + ( - 4 – 9 + 5 ) ] C = ……………………………………………. C = ……………………………………………… C = ………………………….. |
|
||||||||||||||||||||||||||||||||||
|
|
2°) Suppression des parenthèses puis des
crochets. C = [ ( 9 – 5 + 2 ) - ( - 7 + 4 + 6) ] - [
- ( 9 – 3 – 4 ) + ( - 4 – 9 + 5 ) ] ……………………….. ………………………………………………………….. ………………………………………………………………………………………. ; …………………………………………………………………………………….. |
|
||||||||||||||||||||||||||||||||||
|
|
3°) Suppression des crochets puis des
parenthèses. |
|
||||||||||||||||||||||||||||||||||
|
|
C = [ ( 9 – 5 + 2 ) - ( - 7 + 4 + 6) ] - [
- ( 9 – 3 – 4 ) + ( - 4 – 9 + 5 ) ] C = ………………………………………………………………………………. C = …………………………………………………………………………… C = ……………………………………………………. C = ………………………………… |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Activité n° .2. |
|
||||||||||||||||||||||||||||||||||
|
|
Calculez
(simplifiez) l’égalité
« B » ; ( |
|
||||||||||||||||||||||||||||||||||
|
|
·
Appliquez la 1ère méthode : Enlevez les parenthèses
puis les crochets. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
·
Appliquez la 2ème
méthode : Enlevez les crochets puis les parenthèses. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Activité n° 3 |
|
||||||||||||||||||||||||||||||||||
|
|
C = Supprimez crochets et parenthèses (dans
l’ordre de votre choix) C = …………………………………………………………………………………………………. C = …………………………………………………………………………………………………… Regroupez entre elles les fractions de même
dénominateur : C
= Terminez le calcul (commencez à l’intérieur
des parenthèses ) et simplifiez . ……. |
|
||||||||||||||||||||||||||||||||||
|
|
Fiche 8 :
Exemples d’utilisation des nombres relatifs et des sommes algébriques. |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
1°) Calculs d’une moyenne . |
|
||||||||||||||||||||||||||||||||||
|
|
(soit une moyenne de note par exemple ) ·
Moyenne de 12 et 18 :
( 12 + 18 ) ·
Moyenne de 8 ; 15 ; 4 :
( 8 + 15 + 4 ) ·
Calculez la moyenne de : 11 ; 8 ; 4 ;
18 ; 7 ; 15 ; 9 ; vous trouvez : ……………( ………. |
|
||||||||||||||||||||||||||||||||||
|
|
Remarque 1 : Il est possible que la
division « ne tombe pas juste » . Exemple : faîtes la moyenne de 13 ; 6 ; 18 :
( 13 + 6 + 18 ) La division ne se termine pas. Vous obtenez
environ : 12 , 33 Dans le cas d’une moyenne de notes , on arrondirait à « 12 » ou
« 12,5 » |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
2°) Moyenne de nombres relatifs. |
|
||||||||||||||||||||||||||||||||||
|
|
Moyenne de ; - 3 ; 7 ; -
4 ; 9 ; - 2 ; 5 ; ………………….. ( - 3 + 7 – 4 + 9 – 2 + 5 ) |
|
||||||||||||||||||||||||||||||||||
|
|
Remarque 2 : Il se peut que la somme soit un nombre
relatif négatif , dans ce cas , pour calculer la moyenne , vous effectuez la
division sans vous occuper du signe et vous attribuez le signe
« - » au résultat. (cette règle sera justifiée dans la suite
de cette fiche ) . Exemple ( -
24 ·
Moyenne de : 1 ; - 9 ; - 7 ; 3 : …. ( +
1 – 9 – 7 + 3 ) Activité n°1.. Calculez la moyenne de :
- 7 ; 5 ; - 4 ; - 8 ; - 6 ; 3 ; -
5 ; 2 ………………….vous trouvez : … |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
3°) Autre façon de calculer une moyenne. Souvent, vous calculez la moyenne de vos
notes pour savoir si vous avez plus ou moins de « 10 ». Supposez que vous avez obtenu les
notes suivantes ; 5 ;
12 ; 18 ; 15 ; 9 ; 17 ; 8 ; . Par rapport à « 10 » : la
note « 5 » vous fait perdre
« 5 » points, c'est-à-dire « -5 » Par rapport à « 10 » : la
note « 12 » vous fait gagner « 2 points », c'est-à-dire
« +2 » Aussi, complétez le tableau donnant l’écart
de vos notes par rapport à « 10 ». |
|
||||||||||||||||||||||||||||||||||
|
|
Notes |
5 |
12 |
18 |
15 |
9 |
17 |
8 |
|
|
|
|||||||||||||||||||||||||
|
Ecarts |
.-5 |
+2 |
+8 |
+5 |
.-1 |
+7 |
.-2 |
|
←Somme |
|||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
La somme des gains ou des pertes ( par rapport à « 10 » ) est alors …… « 14 » …….. Ce gain ( ou cette
perte) total est à répartir sur les « 7 » notes. Votre moyenne est alors de : 10 + ( .. Vérifiez en calculant la moyenne par la première méthode ,
vous trouvez : ….. |
|
||||||||||||||||||||||||||||||||||
|
|
Remarque 3 : Dans la deuxième ligne du tableau, si l’on enlève les traits
verticaux, on obtient : |
|
||||||||||||||||||||||||||||||||||
|
|
|
.-5 |
+2 |
+8 |
+5 |
.-1 |
+7 |
.-2 |
= 14 |
|
||||||||||||||||||||||||||
|
|
Nous
sommes en présence d’une somme
algébrique ( les signes d’addition sont en
sous-entendus) |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Activité n°2 : On
vous demande de calculer la moyenne de : 5 ;
8 ; 14 ; 16 ;
4 ; 12 ;
7 ; 6 . Ecart
de rapport à « 10 » : ……………………… - 5 ; - 2 ; +
4 ; + 6 ; - 6 ; + 2 ; - 3 ; - 4 ; ← soit la somme = -
8 La
moyenne est alors de : 10
+ ( …… -
Calculez de même la moyenne de 8 ; 13 ; 15 ;7 ; 1 ;9 ;6 11 ; 3 ; 2 ; vous trouvez …………………. : ……… |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
4°) Calcul
mental de la moyenne. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Exemple : |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
Variation des écarts |
|
Variation des écarts |
|
Variation des écarts |
|
Variation des écarts |
|
Variation des écarts |
|
|
|
|
|||||||||||||||||||||
|
|
Notes |
16 |
|
8 |
|
15 |
|
6 |
|
13 |
|
11 |
|
|
|
|||||||||||||||||||||
|
Ecarts |
+6 |
|
-2 |
|
+5 |
|
-4 |
|
+3 |
|
+1 |
|
||||||||||||||||||||||||
|
|
|
+4 |
|
+5 |
|
-4 |
|
+3 |
|
+1 |
|
|||||||||||||||||||||||||
|
|
sommes |
|
+4 |
→ |
+9 |
→ |
+5 |
→ |
+8 |
→ |
+9 |
|
Somme finale
= +9 |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
La
moyenne est alors « 10 + ( ………..
) = 10 + …….. = ……… .
Vérifiez par la 1ère méthode : …… |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Activité n° 3…. |
|
||||||||||||||||||||||||||||||||||
|
|
Calculez
mentalement la moyenne de : 8 ; 6 ; 13 ; 15 ;
7 ; 4 ; 5 ; 2 ; 12 ; …………. vous trouvez :
………………………. Et
calculez la moyenne de : 12 ;
13 ; 5 ; 7 ; 8 ; 15 ; 6 ; 14 ; 16 ;
9 ;8 :
.vous trouvez : ………………………… |
|
||||||||||||||||||||||||||||||||||
|
|
Fiche
complémentaire : Calcul des coordonnées du milieu d’un segment. |
Info +++@ ..les coordonnées
du milieu d’une droite (segment) |
|
|||||||||||||||
|
|
I ) Milieu d’un segment sur une droite
graduée : |
|
||||||||||||||||
|
|
« A » et « B » sont deux points d’une
droite graduée. Le
point « A » a pour abscisse ( -3) et le point « B » ( + 7). Placez
sur la droite ci-contre le point
« M » milieu du segment noté : [ AB] Donnez
l’abscisse de ce point : M a pour abscisse ( + 2 ) |
|
|
|||||||||||||||
|
|
Vérifiez
que cette abscisse est égale à la demi-somme des abscisse
de « A » et « B ». ( C'est-à-dire à la
demi –somme des abscisses ) soit |
|
||||||||||||||||
|
|
Cas général : Etant
donné deux points « A » et « B » d’une droite graduée et
« M » le milieu de [ AB] , appelons
« |
|
||||||||||||||||
|
|
On
écrit : AM
= MB = |
|
|
|||||||||||||||
|
|
En
désignant par « B » celui des points qui a la plus grande abscisse,
on a : Exprimons « On a
alors : ou
encore : |
|
||||||||||||||||
|
|
A retenir . L’abscisse
du milieu d’un segment est égal à la demi-somme des abscisses des extrémités
de ce segment . |
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
Activité n°1… |
|
||||||||||||||||
|
|
Complétez
le tableau suivant : |
|
||||||||||||||||
|
|
|
Abscisse du premier point |
12 |
8 |
-5 |
4 |
-7 |
|
||||||||||
|
|
Abscisse du second point |
4 |
-5 |
-7 |
-3 |
4 |
||||||||||||
|
|
Abscisse du milieu. |
|
|
|
|
3 |
-5 |
|||||||||||
|
|
|
|
||||||||||||||||
|
|
II ) Calcul des coordonnées du milieu d’un segment . |
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
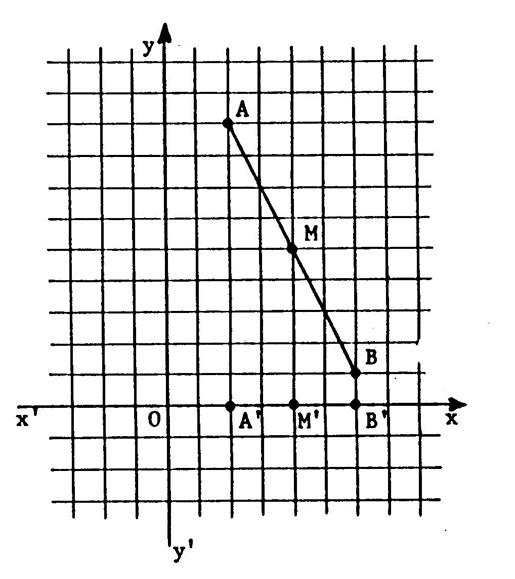
Soient : Deux
axes de coordonnées : Ces
deux axes sont perpendiculaires et on le même
origine « O ». Le
point « A » a pour« coordonnées (+2) , (+ 9) . On
écrit A ( 2 ;9). Le
point « B » a pour« coordonnées (+6) , (+ 1) . On
écrit A ( 6 ;1). Le
point « M » est le milieu de [ AB]
. Nous
allons déterminer ses coordonnées . Considérons
la projection
orthogonale sur -
Le point "A" a pour projeté le point « A’ » sur l’axe -
Le point "B" a pour projeté le point « B’ » sur l’axe -
Le point "M" a pour projeté le point « M’ » sur l’axe D'autre
part , puisque « M » est le milieu de [
AB] , son projeté « M’ » est
le milieu de [ A’B’]. ( voir
la propriété 7 vue dans la fiche « 3 » de cette
leçon) |
|
|
|||||||||||||||
|
|
Donc
l’abscisse de « M’ » est la
demi-somme des abscisses de
« A’ » et
« B’ ». Donc
l’abscisse de « M » est la
demi-somme des abscisses de
« A » et
« B ». C'est-à-dire ( abscisse de
« M ») = On
ferait de même pour les ordonnées, on dira
alors : C'est-à-dire ( ordonnée de « M ») = |
|
||||||||||||||||
|
|
A retenir : Relativement
à un système d’axes de coordonnées , pour tout
segment, l’abscisse du milieu est égale à la demi-somme des abscisses des
extrémités , l’ordonnée du milieu est égale à la demi-somme des ordonnées des
extrémités. |
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
Activités n°2 .. |
|
||||||||||||||||
|
|
Complétez
le tableau ci-dessous : |
|
||||||||||||||||
|
|
|
Coordonnées des 2 points. |
( - 5 ; +2
) |
( - 8 ; -
1) |
( - 5 ; +
3 ) |
|
|
|
||||||||||
|
|
( + 9 ; -
3) |
( + 3 ; +
7 ) |
|
( + 8 ; -
3 ) |
|
|||||||||||||
|
|
Coordonnées du milieu. |
|
|
( - 6 , - 3 ) |
( + 5 ;
- 5 ) |
|
||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|||||||||||||||||
TRAVAUX AUTO FORMATIFS : voir les activités des fiches spécifiques….
|
1° ) Que signifie: Développer ? |
|
|
2° ) Donner la condition minimum permettant
de faire un développement. |
|
|
3° ) Donner le modèle mathématique
représentant ce minimum. |
|
|
4 ° )Donner le modèle mathématique sur le développement de (
a + b ) ( c + d ) |
|
|
I ) Développer les expressions suivantes : |
|
|
|
Série 1 |
résultat |
|
|
9 ( 3 + 5 ) = (pour cet exercice uniquement ne pas effectuer les
calculs!!) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Série 2 |
|
|
|
|
|
|
|
|
|
|
|
Série 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Série 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a (a b
+ c2 f ) |
|
|
|
|
|
|
|
|
|
|
II ) Développer les expressions
suivantes et réduire et ordonner quand cela est possible : Nota pour « réduire » il faut avoir fait « factoriser »,il
vous faudra reprendre ce travail qu’après avoir traité cet objectif !
|
Série 2 |
développer |
Réduire |
Ordonner |
|
( x +1 ) ( x -2 ) = |
|
|
|
|
x +5 ) ( 3x -2 ) = |
|
|
|
|
( -4x +3 ) ( 5
x - 6 ) = |
|
|
|
|
Série 3 |
développer |
Réduire |
Ordonner |
|
( x +5 ) ( x + 5 ) = |
|
|
|
|
( x -5 ) ( x - 5 ) = |
|
|
|
|
( x +5 ) ( x
- 5 ) = |
|
|
|
|
Série 4 |
développer |
Réduire |
Ordonner |
|
( 2x +3 )2 = |
Voir les I.R. |
|
|
|
( -3x +1 ) 2 = |
Voir les I.R. |
|
|
|
Série 5 |
développer |
Réduire |
Ordonner |
|
( a + b )2 = |
Voir les I.R. |
|
|
|
( a - b )2 = |
Voir les I.R. |
|
|
|
( a + b ) ( a - b ) = |
Voir les I.R. |
|
|
Développer , réduire , ordonner
|
|
|
A = (x +5 ) ( 2 x – 1 )
– 3 (2x – 5 ) |
|
Géométrie
|
Calculer l'aire d'une surface |
Longueur |
largeur |
|
|
Rectangle |
L = x +a |
l = x - b |
|