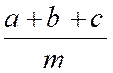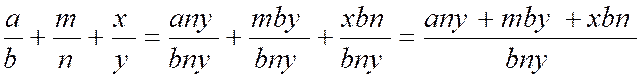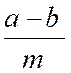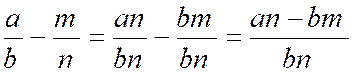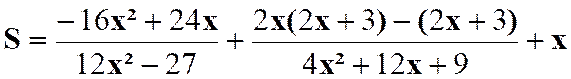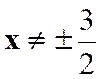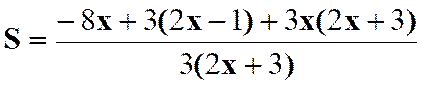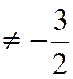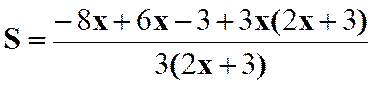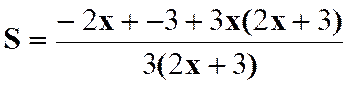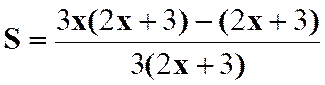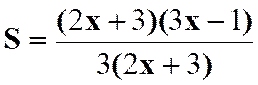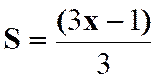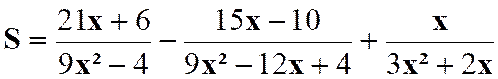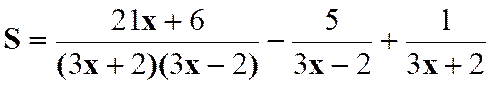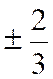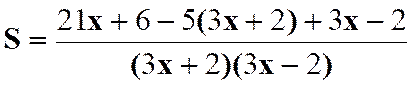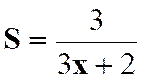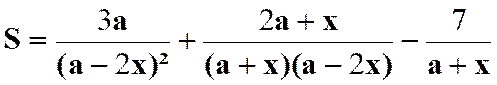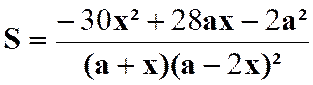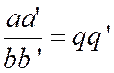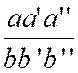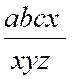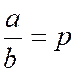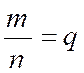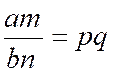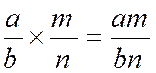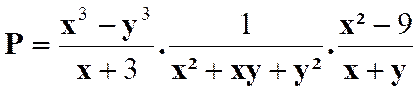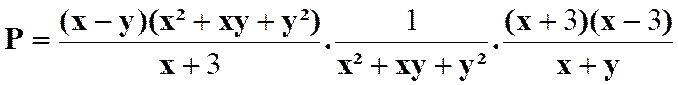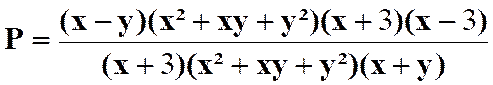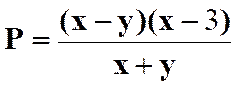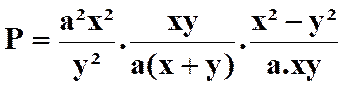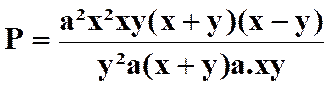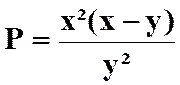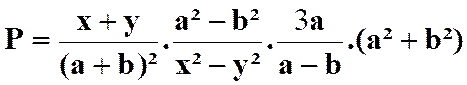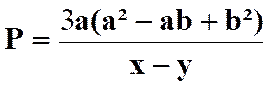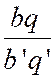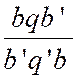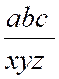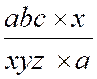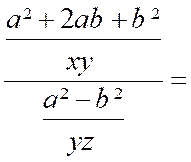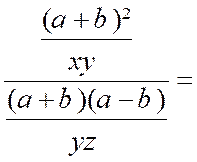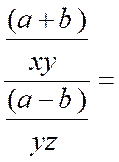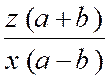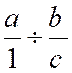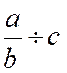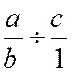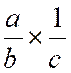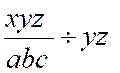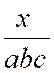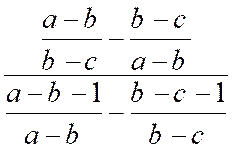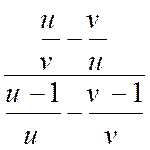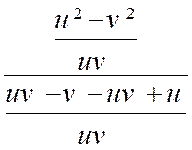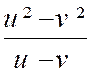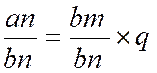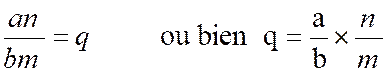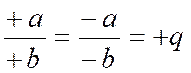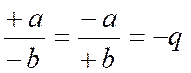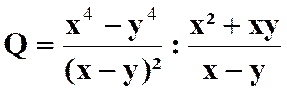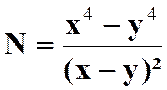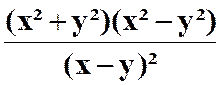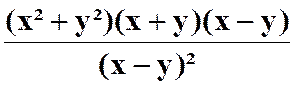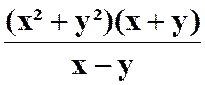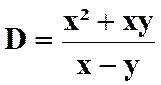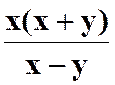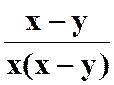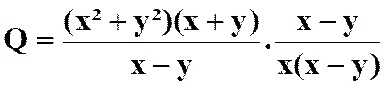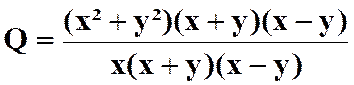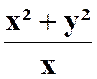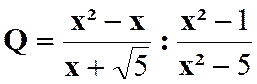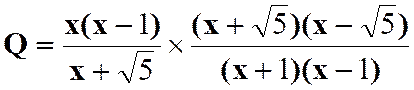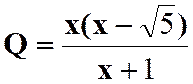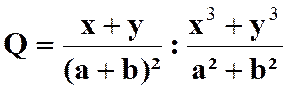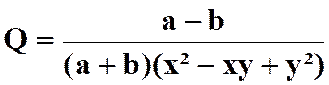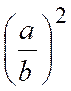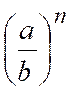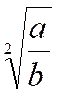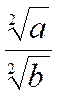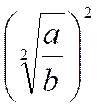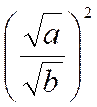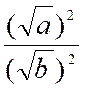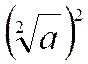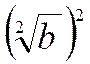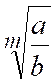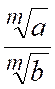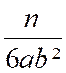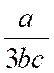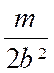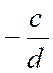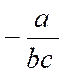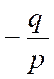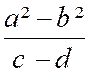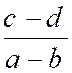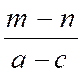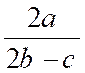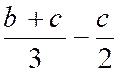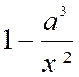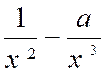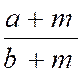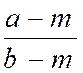1.     voir cas : L’addition de fractions.

2.    Voir cas :La soustraction de deux fractions.

3.   SOMME ALGEBRIQUE DE FRACTIONS .

4.   La multiplication de fractions.

5.   La division de fractions (fraction de fraction).

6.   Elévation d’une puissance une fraction.

7.   Extraire la racine d’une fraction.

Les opérations sur les « quantités fractionnaires » sont les mêmes opérations que sur les fractions entières / Les définitions générales de ces six opérations , telles  qu’on les a énoncés ( en pré requis) restent applicables aux calculs sur les quantités fractionnaires.

Info Arit.

1 -  ADDITION DE FRACTIONS :

Règle :   Pour ajouter (additionner)   plusieurs  fractions entre elles, il faut les réduire d'abord au même dénominateur, faire ensuite la somme des numérateurs et donner à cette somme le dénominateur commun ; ainsi :

Démonstration :

Soient  les fractions :  ;  ; , réduite au même dénominateur  , et soient « q » ; « q’ » ; « q’’ » , leurs valeurs respectives .

 On a « = q »    ; « = q’ »   ;= q’’ »  , de là :    « a = m q » ; «b= m q’ » ; «c = m q’’ »

Additionnant membre à membre  , on trouve : « a + b + c = m ( q + q’ + q’’ ) »  d’où enfin  « = q + q’ + q’’ =  +  + »

Addition de fractions qui n’ont pas le même dénominateur .  ( on doit réduire au même dénominateur avant d’additionner)

Info Arit.

2 - SOUSTRACTION  DE FRACTIONS :

Règle : Pour soustraire deux fractions l’une de l’autre , on les réduit au même dénominateur, on soustrait les numérateurs l’un de l’autre et l’on donne à la différence le dénominateur commun.

La règle ne s’applique qu’à deux fractions …….

Démonstration :

Soient  les fractions :  ;  ;  proposée .  réduite au même dénominateur  , et soient « q » ; « q’ » ; « q’’ » , leurs valeurs respectives .

 On a « = q »    ; « = q’ »   ; de là :    « a = m q » ; «b= m q’ » ;

Soustrayant  membre à membre  , on trouve : « a -  b  = m ( q -  q’  ) »  d’où enfin  « = q -  q’  =  -   »

La soustraction ne peut s'opérer sur les numérateurs qu'après toutefois que les deux fractions ont été réduites au même dénomina­teur ; on aura donc

3-  SOMME ALGEBRIQUE DE FRACTIONS .

Procédure :

1°) On les réduits au même dénominateur.

2°) On forme la somme algébrique prescrite , sur les numérateurs des fractions modifiées.

3°) On adopte pour dénominateur le dénominateur commun.

4°) On regarde si le résultat peut être simplifié.

Exemples :

Calculer la somme :

N°1 :          avec 

Solution : Les fractions ont été simplifiées et réduites au même dénominateur dans le cours : (COURS SUR ) donc

Nous écrirons :

                avec x

  =  

Le résultat simplifié  peut donc être :                   avec x

N°2 :  Calculer la somme : 

Indications : Simplification des fractions :   avec  x   0 et  x 

Réduction au même dénominateur :

Résultat :

N°3 :  Calculer la somme :         avec  x   -a  et  x 

Réponse (solution) 

Info arith. Mul.

4 -  MULTIPLICATION  DE FRACTIONS :

Règle : Pour multiplier deux ou plusieurs fractions entre elles , on multiplie les numérateurs entre eux et les dénominateurs entre eux ;

Démonstration :

Soit   x  .    En posant  = q  et   =q’ ; on a  « a = bq » et « a’=  b’q’ » 

Multipliant membre à membre ces dernières égalités , on obtient :  « aa’ = bqb’q’ »  , ou  « aa’= (bb’)(qq’) ; divisant de part et d’autre par « bb’ » ; on a   «  »   ou   «  = x »

La  règle s’étend au cas de trois , de quatre , d’un nombre quelconque de fractions ; car on a «x x = x=   et ainsi de suite.

Corollaire : Pour multiplier entre elles une fraction et une quantité entière , on multiplie le numérateur de la fraction par cette quantité entière :

 x c  =   x   =    =

On arrive à un résultat tout simplifié en divisant , si cela est possible ., le dénominateur de la fraction par la quantité entière , ainsi , l’on aurait :

«  . x  =      »   ; car   «  . x  =  =  »  

Procédure pour multiplier des fractions.

1°) simplifier les fractions s’il y a lieu.

2°)faire le produit terme à terme ( numérateurs entre eux , dénominateur entre eux.

3°) Simplifier le résultat s’il y a lieu.

On fait le produit de plusieurs fractions en multipliant les numérateurs entre eux et les dénominateurs entre eux.

Soient les deux fractions   et   : représentons la   valeur de la première par p, celle de la seconde par q,   ,   et posons         et 

 ce qui donne a = bp    et  m =  nq      

Mais si les deux quantités a    et m       sont respectivement égales aux deux autres bp et nq, le produit , des deux premières égalera aussi le produit des deux autres, et l'on aura :

          a  x m = bp x  nq, ce qui revient à    am   =  bn x pq ; et enfin, en divisant par la   .quantité    bn, on aura :

  donc

Exemples :

• Exercice n°1 : Effectuer le produit.

             avec  x   - 3    et   avec  x  - y

Solution :

Pour savoir si les fractions peuvent être simplifiées , il faut  décomposer les termes en produits de facteurs. On a ainsi :

Faire les produits terme à terme :

Simplifier par ( x + 3 )   avec  x  -3 ;  et par ( x² + xy + y² ) qui n’est jamais nul (on le verra ultérieurement) sauf pour « x = 0 » ; y = 0 .

Il reste : 

• Exercice n°2 : Effectuer le produit.

Indications :    simplifier par «  a² ; x ; y ; ( x + y ) »

Réponse :

            avec    a   0 ;  x  0 ; y 0 ; x + y 0

• Exercice n°3 : Effectuer le produit.

Réponse :

              avec   a  b     et    x  y

Info.arith. div

5 -  DIVISION ( dit aussi : Quotient )   DE FRACTIONS :

PARTIE 1 :

Rappel : inverse.

Règle : Pour diviser  deux fractions l’une par l’autre , on multiplie la fraction dividende par l’inverse de  la fraction diviseur.

·       On rappel que l’inverse de «  »  est  «  » et que l’inverse de  « m » est  «  »

.

 Démonstration 1  :Nous disons que  : =    car ; si l’on multiplie  par la fraction diviseur  ; on retrouve la fraction dividende .

Démonstration 2 : on pose «   = q »   et   «  = q’ » , et , par suite  « a = bq »  et « a’= b’q’ » ; puis divisant membre à membre ces deux dernières égalités , on a :  =  ; et en multipliant par  les deux membres , il vient =   soit l’égalité =

Autres explications : On arrive à un résultat tout simplifié en divisant , lorsque c’est possible , les numérateurs entre eux et les dénominateurs entre eux. Ainsi , l’on aurait immédiatement :    =  , en effet    = =

Par conséquent, lorsque l’on a deux fractions à diviser l’une par l’autre et qu’on aperçoit des facteurs communs aux deux numérateurs ou bien aus deux dénominateurs , on les supprime immédiatement.

Exemple :

Corollaire :

N°1 : Pour diviser une quantité entière par une fraction , on multiplie cette quantité par la fraction renversée :   =     = 

N°2 : Pour diviser une fraction par une quantité entière  , on multiplie le dénominateur de la fraction par cette quantité :

car on a  =   =    =  ; Ou bien , s’il est possible , on divise le numérateur de la fraction par cette quantité :

exemple :  =

Remarque : L’emploi de « lettres auxiliaires simplifie parfois avantageusement les écritures et les calculs.

Soit , par exemple , à effectuer les opérations :  F =

En posant :  « a -b=u »   et « b -c=v » , on a :

F =    =  == u+v

D’ où : « F = u+ v = a – b +b -c = a – c »

Conclusion : F =  a – c

Partie  n° 2 :

On effectue la division d'une fraction par une autre en multipliant la fraction dividende par la fraction diviseur renversée,

Soit à diviser les deux fractions    par       et représentons le quotient  par q    ; nous aurons :       :     =   q  

Ou bien  ( en multipliant à gauche et à droite ; les deux membres par   )     on peut écrire :      =   q   x 

En réduisant au même dénominateur, on tire de là : 

<ft supprimant le dénominateur commun bn, on ne  troublera pas l'égalité, et l'on aura :      an = bm x q  ; * enfin, en divisant de part et d'antre par bm, cette der­nière égalité donne :

ce qui prouve la règle énoncée.

Remarque.  Dans les démonstrations ci-dessus nous avons admis que les deux termes des fractions proposées étaient positifs ; mais, s'il en était autrement, la règle n'en serait pas moins vraie,

    Il est important de rappeler à cette occasion que la valeur absolue d'une fraction algébrique est indépendante des signes de ses termes, et que, de plus, cette valeur est positive si les deux termes ont le même signe, et négative s'ils ont des signes contraires, c'est-à-dire qu'on aura, dans la division algébrique (chapitre : règle des signes),

  et   

ce qui prouve que l'on peut changer les signes  des deux termes d'une fraction sans altérer sa valeur.

Exercice 1 : Calculer le quotient :    ( = )

Solution : il est bon de transformer en produit le dividende et le diviseur, ne serait-ce que pour ,éventuellement , les simplifier :

  =  = =    avec  x y

De même :  =  ; son inverse :

Si bien :

Et         =   ;  avec  x  - y

Sont également exclues les valeurs qui annuleraient la fraction diviseur , donc  avec  x  0 et avec  x  - y

Exercice 2 : Calculer le quotient :

Indications : il faut écrire   avec  x  1 ; avec  x -1 ; avec  x  

Réponse :

Exercice 3 : Calculer le quotient :

Réponse :

 ;  avec ab   ;  a - b   ; x -y

Info +++

6 -  ELEVATION  AUX PUISSANCES   UNE  FRACTION :

Info +++

Règle : Pour élever  une fraction au carré et , en général, à une puissance quelconque, on élève chacun de ses deux termes à cette puissance.

Démonstration : Soit à démontrer, pour la racine carré ;la formule  =  x   = 

Et plus généralement :  =  x  x  x  x ………….(« n » fois)  = 

Info++

7 -  EXTRACTION  DES RACINES D’ UNE  FRACTION :

Règle : Pour extraire la racine carrée  et , en général, , une racine quelconque d’une fraction , on extrait la racine de chacun de ses termes. 

Démonstration : Soit à démontrer , pour la racine carrée , la formule :  =  

Si on élève au carré le premier membre =

Si on élève au carré le second membre  on a , =    = 

 Rappels :  = a … et   = b

Les carrés des deux membres de la formule étant égaux , ces deux membres le sont aussi , et la formule est démontrée.

On établirait de même la formule générale :   =   ; en faisant voir que les puissances m^ième  des deux membres sont égales .

Info plus

NOTA : Cette démonstration suppose que « a » et « b » sont positifs et qu’il n’est question que des valeurs positives du radical ; en d’autres termes , on ne considère ici que les racines dites « arithmétiques ».

Définition : « valeur arithmétique » : Si A représente une quantité  positive , on entend par valeur arithmétique du radical   ou « racine arithmétique » n^ième de « A » , le nombre positif qui ,élevé à la puissance « n^ième »  , reproduit la quantité A.

Réduire an même dénominateur les fractions suivantes :  ;  ;

Réduire au même dénominateur les fractions :  ;   et

Ajouter les fractions :   et 

Additionner :   et 8 unités 

Trouver la différence des fractions :  ;

Quelle est la différence de :  à  -x ?

7.    

Quel est le produit de 7 par  ?

Faire  le produit de  par

Diviser la fraction   par 

Trouver le quotient de  par – 9

Multiplier :   par    et simplifier le produit.

Diviser  :   par 

Faire le produit de    par

Diviser    par

Trouver que dans une fraction proprement dite  , c'est-à-dire dans le cas où   a < b  , on a toujours les inégalités :

 <    et   >