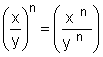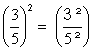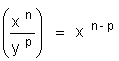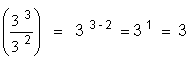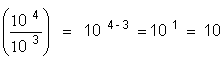Auteur : WARME R. DOSSIER : ELEVE.
NOM : …………………………………			Prénom : ………………………………..	Classe :…………………..
Année scolaire : ……………………………….			Date : ………………………	Formation : Validation : OUI - NON Le :

remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure et confirmer une formation .
Leçon		Titre
N°4		PUISSANCES et RACINES « avec » des nombres décimaux positifs ( D ⁺)
( Info : Ensemble de nombres noté : D+ )
CHAPITRES :					Validation
Carré d’un nombre.					Ÿ
Cube d’un nombre.					Ÿ
Puissance de 10.					Ÿ
Ecriture scientifique d’un nombre.					Ÿ
Racine carrée.					Ÿ
COURS
i9	1° Carré d’un nombre					Cd :i ³INFO
Définition : Le « carré d’un nombre » est le produit de ce nombre par lui-même . Exemple : 3 ² devient le produit 3 ´ 3 ou x ² = x ´ x
Cette écriture est une simplification de l’écriture d’une multiplication d’un nombre par lui même. a) Ecriture normalisée Le « 2 » est appelé : exposant 2 ou puissance 2 ou « carré » X² = X ´ X On multiplie le nombre « x » par le nombre « x » iAttention : en algèbre le signe « multiplié : ´ » n’est plus employé . Il est parfois remplacé par un point , ainsi l’écriture : X ´ X est remplacée par X .X ou par la nouvelle écriture : X²

+*Activité 1*
Reconnaître l’écriture d’un carré d’un nombre entier Exemple 1 : calculer 3² 3² s’écrit aussi 3 3 ( = 9 ) Remarque : le carré d’un nombre entier est appelé : « carré parfait » Le calcul se fait de tête : calcul mental ; Le calcul ne peut se faire de « tête » .Il faut poser la multiplication !
+*Activité 2*
Reconnaître l’écriture d’un carré d’un nombre décimal Exemple 2 : calculer 3,45 ² 3,45 ² = 3,45 3,45 ( = 11,9025 ) Remarque : En l’absence de calculatrice on posera l’opération et l’on fera le calcul . b) Calcul du carré d’un nombre ( pour obtenir le carré d’un nombre on dispose de 3 possibilités) . Solution 1 : on fait le calcul à la main , on pose l’opération et on fait la multiplication de « x » par « x » : Exemple Enoncé : calculer 3,45 ² on pose l’opération :
		3,45 3,45 ----------------- 1 7 2 5 1 3 8 0 . 1 0 3 5 . . ----------------- 1 1, 9 0 2 5

Réponse 3,45 ² =11,9025

Solution 2 : On utilise la calculatrice, on tape la multiplication 3,45 3, 45

Attention : le point remplace la virgule ! ! ! ! !On tape successivement :

Lecture d’écran : 11 . 9025

Réponse 3,45 ² = 11,9025

Solution 3 : On utilise la calculatrice , on se sert de la touche x ²

On peut calculer le « carré » d’un nombre « x » avec la calculatrice avec la touche : x²

Exemple 3: calculer x² avec x = 13, 24

soit x ² = 13,24 ²

On tape sur les touches successivement :

Attention : le point remplace la virgule ! ! ! !

x²

175.2976

175. 2976 ,lorsque l’on reportera le résultat il faut remplacer le point par la virgule .

On écrira donc : 13, 24 ² = 175,2976

APPLICATIONS courantes : (@ info plus)

► Les unités :

(1 1 m) fois ( 1 1 m) = (1 1 m ) ( 1 1 m ) = 1 ² 1 m ² = 1 m ²

ce qui fait dire que :

si l’on multiplie des mètres par des mètres on obtient des mètres carrés que l’on note m m = m²

► Aire du carré : A = c² ; si « c » = 3 m alors c² = ( 3 m ) ² soit A = 9 m²

► Aire d’un disque :

A = 3,14 R² ; si R = 3 m alors A = 3,14 3 m 3 m ; A = 28,26 m²

2°) Cube d’un nombre

Cd :i ³ INFO plus ! ! ! ! : 2

Définition :

Le « cube d’un nombre » est le produit de trois facteurs (³) égaux à ce nombre

. Exemple : l’ écriture « 3 ³» devient le double produit de 3 3 3

au lieu d’écrire 3 3 3 on préférera l’écriture «3 ³» ; cette écriture est une simplification de l’écriture d’une multiplication d’un nombre par lui même par lui même.

Calculs : On doit faire une double multiplication :

Exemple :pour 5 ³ on calcule d’abord 5 fois 5 (= 25) , puis on multiplie le résultat « 25 » par 5 ; = 125

Ainsi : 5 ³ = 5 5 5 = 25 5 = 125

énoncé

traduction

Résultat des calculs

5 ³

5 5 5 = 25 5 =

125

3,2 ³

3,2 3,2 3,2 = 10,243,2 =

32,768

APPLICATIONS courantes : (@ info plus)

► Les unités : (on reverra la notion sur la « grandeur »)

(1 1 m) fois ( 1 1 m) fois ( 1 1 m) = (1 1 m ) ( 1 1 m ) ( 1 1 m)

= 1 ³ 1 m ³ = 1 m ³

ce qui fait dire que :

si l’on multiplie des mètres par des mètres par des mètres on obtient des mètres « cubes » que l’on note m m m = m ³

► Volume du cube : V = c ³ ; si « c » = 3 m alors c³ = ( 3 m )³ soit V = 27 m ³

► volume d’une sphère :

V = (4/3 ) 3,14 R ³ ; si R = 3 m

alors V = (4/3 ) 3,14 3 m 3 m 3 m ; V = 113 , 04 m³

Chapitre 3 : Info + sur : « Les Carrés d’opérations simples ».

Commentaire :

Il faut travailler la leçon : « Les Carrés d’opérations simples ».

(découverte des I.R. Identités Remarquables) pour obtenir le niveau V

On se souviendra que lorsque l’on applique le théorème de Pythagore on obtient obligatoirement une équation de la forme :

a ² = b ² + c ²

qui débouche sur l’extraction d’une racine carrée.

C d info ++++

Chapitre 4 : Info + sur : Les formules sur les puissances

Les formules suivantes sont données pour information

C d info ++++

Formules

Appliquées aux nombres décimaux

Appliquées aux puissances de dix.

( x ⁿ )^p = x ⁿ^p

( 3² )⁵ = 3 ²⁵ = 3 ¹⁰

( 10² )³ = 10 ²³ = 10⁶

x ⁿ x^p = x ^{n + p}

3 ² 3⁵ = 3 ^{2 + 5}= 3 ⁷

10 ² 10⁵ = 10 ^{2 + 5}= 10 ⁷

x ⁿ yⁿ= ( x y )ⁿ

3 ³ 5³= ( 3 5 )³ = 15 ³

Pour plus d’informations sur ces formules cliquer sur C d info ++++

3°) Puissance de 10

:iINFO plus CD ³ ! 3

Cette écriture permet de ne pas être obliger d’écrire des grands nombres (qui est une source d’erreurs)

Exemple : au lieu d’écrire 100000 on écrit 1 10 ⁵ qui est égal à 10 ⁵ : ( on lit « 10 puissance 5 » ou « 10 exposant 5 » )

Cette écriture est la traduction des calculs en chaîne de « 1010 101010 ».

Le résultat est obtenu en faisant le produit de 5 facteurs égaux à « 10 ».

1010 101010 = 100101010 = 10001010 = 10 00010 = 100 000 = 10 ⁵

Ainsi :

Ecriture simplifiée

Qui correspond à la multiplication

Forme décimale :

Si l’exposant est « 5 »

On a 5 facteurs identiques qui est « 10 »

5 zéros derrière le « 1 »

10 ⁵

1010 101010

100 000

Commentaire : cette écriture est une forme simplifiée de la multiplication d’un nombre par lui -même .Elle diminue le risque de transcription d’une longue multiplication.

Il est plus simple d’écrire « 10 ⁵ » que « 1010 101010 »

Exemples :

10⁰= 1 ( par convention )

10² = 1010 = 100 = cent

10³ = 1010 10 = 1000 = mille

10⁴ = 1 0000 ( un 1 suivi de 4 « 0 ») = 10 mille

10⁵ = 100 000 ( un 1 suivi de 5 « 0 ») = 100 mille

10⁶ = 1 000 000 ( un 1 suivi de 7 « 0 ») = 1 million

GENERALISATION :

Par définition :

Ecriture simplifiée

Qui correspond à la multiplication

Forme décimale :

L’exposant est « n »

« n » facteurs égaux à 10

« n » zéros

10 ⁿ

1010 101010…n

« 1 » suivi de « n » zéros

Exemple :

10⁶ = 1 000 000 ( un 1 suivi de 7 « 0 ») = 1 million

( Voir sur C d : applications : les volumes ) et les aires

Cas particuliers : 10 ⁰ = 1 et 10¹ = 10

Cas des puissances négatives : On a également : transformation en forme décimale .

On écrit :	« Se lit »	« peut s’écrire sous forme de produit »	Représente le nombre décimale.
	= 1 divisé par 10	= 1 ´ 10^-1	= 0,1
	= « 1 divisé par 100 »	= 1 ´ 10^-2	= 0 ,01
	= 1 divisé par 1000	= 1 ´ 10^-3	= 0,001
; e t c….. l’exposant « négatif » indique le numéro du rang du chiffre « 1 » à mettre après la virgule . Exemple : Ecrire 10 ^–5sous forme décimale = 0,000 01 ; Le « 1 » se trouve au 5^ème rang .

4°) Ecriture scientifique d’un nombre.

Dans l’écriture scientifique , la partie entière du nombre décimal « a » ne contient qu’un chiffre

Par définition

L’écriture scientifique d’un nombre est l’écriture de ce nombre sous d’une multiplication de la forme « a 10ⁿ » où « a » est un nombre décimal qui s’écrit avec un seul chiffre ( différent de zéro ) avant la virgule .

On dira d’une autre façon :

L’écriture scientifique d’un nombre est l’écriture de ce nombre sous d’une multiplication de la forme « a 10ⁿ » où « a » est un nombre décimal qui possède un seul chiffre ( différent de zéro ) dans la partie entière.

¶ Savoir passer d’une écriture sous forme décimale à une écriture dite « scientifique »

Exemple 1 : Ecrire sous forme scientifique le nombre 90 000

Le nombre décimal 90 000 se décompose sous la forme 9 10 000 pour s’écrire 9 10⁵

Exemple 2 : Ecrire sous forme scientifique le nombre 135 000 :

135 000 = ; On a 135 000 = 1,35 100 000 = 1,35 10⁶

· Savoir passer d’une forme scientifique à une écriture décimale

Exemple : Donner la forme décimale de l’écriture scientifique 7,53 10⁶ .

► 7,53 10⁶ s’écrit 7,53 1 000 000 après calcul on obtient le nombre 7 530 000.

iRemarque : les calculatrices ne peuvent afficher l’écriture scientifique d’un nombre.

On lit sur l’écran 3.69 ⁰³ = 3,69 10³ = 3,69 1 000 = 3 690

( Il faut savoir « traduire » l’affichage d’écran de la calculatrice , elle n’est pas normalisée , c’est une écriture « fabriquant » qui n’est pas en règle avec l’écriture mathématique).

iIntérêt de cette écriture

Exemple on veut calculer 90 000 ´ 1 20 000

Avant de faire ce calcul on transforme : 90 000 s ‘écrit 9´ 10⁵ et 120 000 s’écrit 1,2 ´ 10⁵

On transforme les écritures décimales en écriture « scientifique »

90 000 ´ 1 20 000 devient 9´ 10⁵ ´ 1,2 ´ 10⁵ = 9´ 1,2 ´ 10⁵ ´ 10⁵ = 10,8 ´ 10 ⁵⁺⁵ =10,8 ´ 10 ¹⁰

soit 90 000 ´ 1 20 000 = 10,8 ´ 10 ¹⁰ soit 10 800 000 000 0

( pour savoir plus sur ce type de calcul cliquer ici ³ )

En écriture ingénieur on aurait écrit : 108 ´ 10 ⁹ ;l’exposant de la puissance de « 10 » doit être « 3 » ou un multiple de « 3 » .Le nombre « a » doit être compris entre 1 £ a < 1000

5°) Racine carrée.

:1i ;:2i

3°) Un nombre « incommensurable »

@ info

Exemple :

Si l’on mesure la diagonale « d » d’un carré en prenant comme unité de mesure le côté « a », on ne trouve aucune partie de l’unité « a » contenue un nombre exact de fois dans « d » , on dit qu’il n’y a pas de « commune » mesure entre « d » et « a » , le résultat de la mesure est un nombre incommensurable . Dans le cas de la figure ce nombre est

Dans la pratique des opérations , on se contente d’une mesure approchée de la grandeur donnée et l’approximation varie avec la nature de la mesure à effectuer.

Définition : La racine carrée de « a » est le nombre qui , élevé au carré , donne « a ».

Notation : . on lit « racine de a ».

Pour obtenir la racine carrée d’un nombre on utilise nos connaissances On dispose de 4 possibilités

« on reconnaît un carré parfait » autrement on se sert généralement de la calculatrice ; par ailleurs , il existe la table numérique (³) ; en dernier ressort on peut faire ce calcul « particulier » ,on dit que l’on va : « extraire la racine(³) ».

En règle générale , on utilise la calculatrice :

pour obtenir la valeur d’une racine carrée il suffit de taper sur la touche

Exemples :

Exercice 1 : Donner la racine carrée de 49 . ( notée )

1^ère solution : par déduction

On sait que 49 est le carré parfait de 7 ( 7 7 = 49 = 7² ) : alors on donne la réponse directement := 7

2^ème solution : On utilise la calculatrice :

on tape :

on lit à l’écran 7

Exercice 2 : Donner la racine carrée de 29 (notée )

29 n’est pas un carré parfait , on doit utiliser la calculatrice

On tape on lit à l’écran ( suivant le type de calculatrice):

5,38516480713450403125071049154033……

La valeur arrondie de est , au centième près 5,39

Il est conseillé de comparer le résultat affiché avec le résultat donné dans une table numérique .

Celle ci donne pour un résultat au 0,001 près : 5,385

Document : table des puissances et racines « carrées » .

: Cliquer ici ³ une table numérique.

Généralisation sur les racines

C d :Info +++

· Ecritures équivalentes : = =

· Si a ³ 0 , alors désigne le seul nombre qui a pour carré « a ».

Exemples

« 16 » est un nombre positif , le nombre positif qui a pour « carré » « 16 » est « 4 ».

On sait que : ( 4² = 4 ´ 4 = 16 ) ;

On dit que « 4 » est la racine carrée de « 16 » et on écrit : = 4

21 est un nombre positif , sa racine carrée n’est ni un nombre entier ni un nombre décimal , ni une fraction , on l’écrit :

iCe nombre qui n’est ni un nombre entier , ni un nombre décimal , ni une fraction est appelé : nombre « irrationnel ».

· Si a ³ 0 , alors () ² = a

· Si a ³ 0 , alors est la solution positive de l’équation x² = a

Conséquences :

· Si k ³ 0 , alors = k et , si k £ 0 , alors = - k

Exemple : ( + 4 ) ² = (+16 ) et ( - 4 )² = ( + 16 ) aussi si l’on fait la racine carré du nombre relatif ( +16) : on trouve deux solutions possibles :

= ( + 4 ) ou ( - 4)