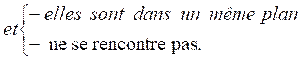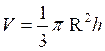III) LECON Rappels sur : la géométrie dans l'espace en 3^ème

Chapitres :

i9	TITRE :	:i
i9	DROITES et PLANS	:i
	PARALLELISME :
	A) Droite et plan.
	B) Si une droite « D » a deux points A et B dans un plan elle est contenue dans ce plan.
	C) Plans parallèles coupés par un plan.
	PERPENDICULARITE.
	A) On démontre et on admettra que la droite D est orthogonale à toutes les droites du plan P.
	B) Pour savoir qu’une droite D est perpendiculaire à deux droites du plan « P » passant par «  pour en déduire qu’elle est perpendiculaire à « P ».
	C) Droites perpendiculaires et plans parallèles.
	D) Etant donné un plan  « P » et un point O de l’espace, il existe une droite perpendiculaire à « P » passant par A et une seule.
i9	VOLUMES	:i
	Sphère.
	Pyramide régulière.
	CONE DE REVOLUTION.

>>>Aide pédagogique

En RESUME

i9

DROITES et PLANS

:iAprès

Parallélisme.

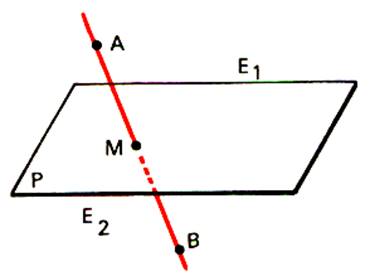
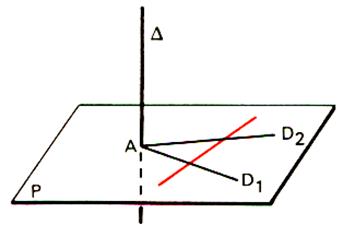
A) Droite et plan.

Lorsqu’une droite et un plan n’ont qu’un point commun on dit qu’ils sont sécants. La droite (A B) joignant A de E1 et un point B de E2 admet un point commun et un seul « M » avec le plan P

B) Si une droite « D » a deux points A et B dans un plan elle est contenue dans ce plan.

Deux droites D et D’ de l’espace sont parallèles lorsque :

Deux droites parallèles à une même droite sont parallèles entre- elles :

- Si D est // à D et D’ // D alors D et D’ sont //

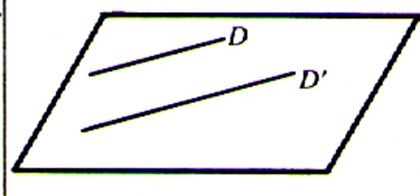
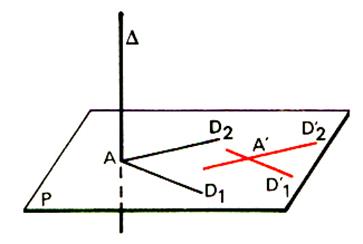
C) Plans parallèles coupés par un plan.

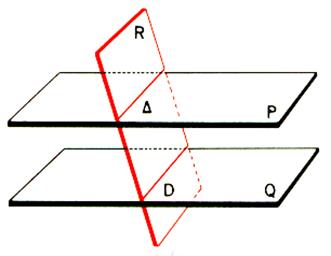
Lorsque deux plans sont parallèles, tout plan ( R ) qui coupe l’un coupe l’autre et les droites d’intersections sont parallèles : Si P // Q alors D // D

Avant

PERPENDICULARITE.

« perpendicularité »

A) On démontre et on admettra que la droite D est orthogonale à toutes les droites du plan P.

Si D est perpendiculaire au plan « P » signifie que : - D et « P » sont sécants en « A ». - D est perpendiculaire à toutes les droites de « P » passant par A

B) Pour savoir qu’une droite D est perpendiculaire à deux droites du plan « P » passant par «  pour en déduire qu’elle est perpendiculaire à « P ».

Si D ^ D1 et si D ^ D2 Alors D ^ P

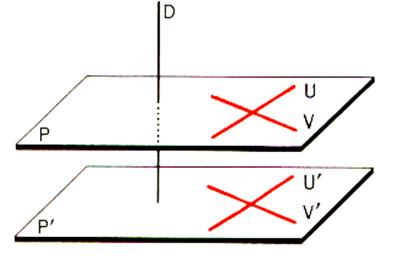
C) Droites perpendiculaires et plans parallèles.

Lorsque deux plans parallèles, toute perpendiculaire à l’un est perpendiculaire à l’autre.

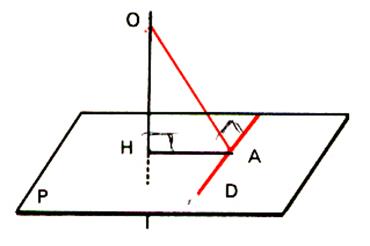
D) Etant donné un plan  « P » et un point O de l’espace, il existe une droite perpendiculaire à « P » passant par A et une seule.

OH est perpendiculaire au plan « P » .

VOLUMES

avant.

Sphère.

Suite.

· Le volume d’une sphère est : 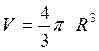et son aire est A = 4 p R²

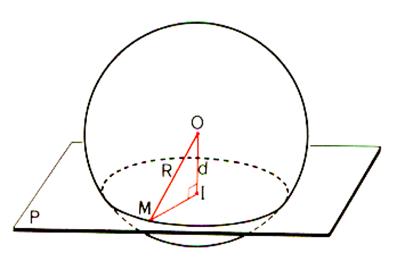
· Section d’une sphère.

Soit une sphère de centre « O » et de rayon « R » et un plan sécant à la sphère.
Soit OI = d la distance du centre « O » au plan « P ». Soit M un point d’intersection de la sphère et du plan. On a dans un triangle rectangle OIM : IM^2 = OM^2 – OI^2 = R²- d² ( = 90°) Donc : IM = (cliquer ici : pré requis : Pythagore)

Le point « I » est le projeté orthogonal de 0 sur « P ».

- le plan P coupe la sphère si et seulement si 0I< R .

Dans ce cas l’intersection est un cercle de rayon r = IM ;

- le plan « P » est tangent à la sphère si OI = R

Avant

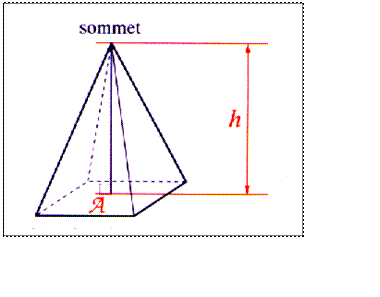
Pyramide régulière.

Suite.

Une pyramide est dite irrégulière si : -sa base est un polygone régulier ; - le projeté orthogonal de son sommet est le centre du cercle circonscrit au polygone de base. Le volume de la pyramide est : « base » : aire du polygone de base.

S B B

La droite (SA) est perpendiculaire à la base. Le segment [SB] est la hauteur du triangle elle est l’apothème de la pyramide.

Remarque : SB² = SA² + AB²

Avant

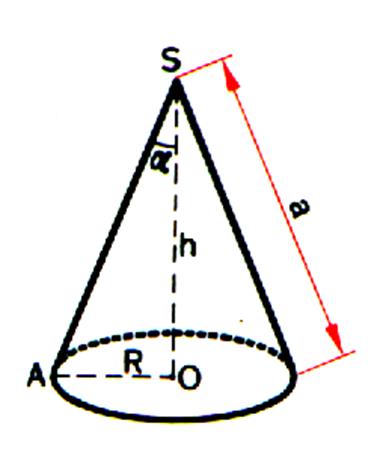
CONE DE REVOLUTION.

Suite.

Il est obtenu par la rotation d’un triangle SOA , rectangle en O autour de l’un des côtés de l’angle droit ( ici (SO))

Le volume du cône est OA = R ; SA= a ; SO = h ; a² = R² + h² La droite (SA) est appelé « génératrice » du cône .Le segment [SA] est l’ apothème du cône. SO est la hauteur ; est l’angle générateur. Toute section parallèle à la base est un cercle.

Leçon	Titre
	TRAVAUX d’Auto - FORMATION sur La géométrie dans l’espace.

Voir cas par cas.

TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE

TRAVAUX N° d ‘ AUTO - FORMATION EVALUATION