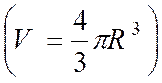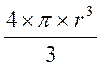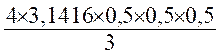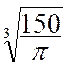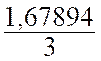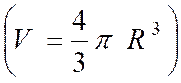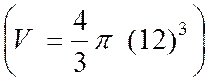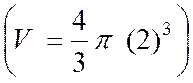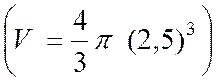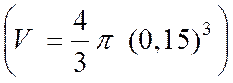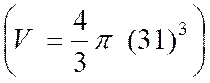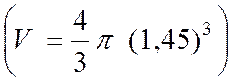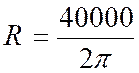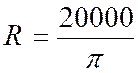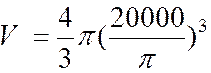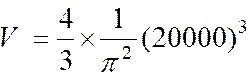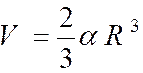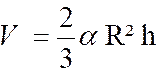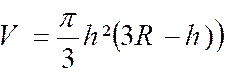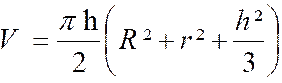|
|
|
|
|
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : |
Objectif
suivant : |
|
|||
|
|
|||||
|
|
DOSSIER : SPHERE ( 3 /3 ): calcul d’aire et volume |
|
|||
|
|
1.
Aires ( sphère
et fuseau , zone sphérique et calotte sphérique ) |
|
|||
|
|
2. volume
d’une boule ( sphère) |
|
|||
|
|
3. ( sphère et onglet ; secteur sphérique, segment sphérique ) |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
TEST |
COURS |
1°)Interdisciplinarité : 3°)
A la fin des travaux auto formatifs vous trouverez des problèmes |
|
|
|
|
||||||||||||||||
|
|
|
|
|||||||||||||||
|
|
RAPPEL : |
|
|||||||||||||||
|
|
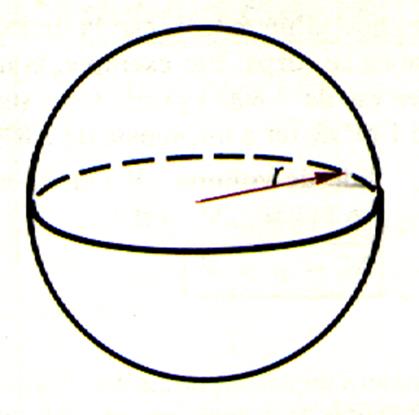
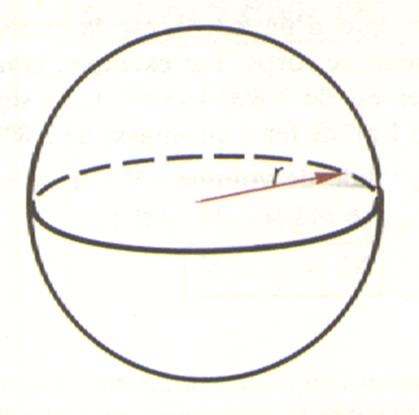
Une sphère est un solide limité par une surface courbe dont tous
les points sont équidistants d’un point intérieur appelé
« centre ». Rayon d’une sphère : Le rayon « r » de la sphère est une droite qui va
du centre à un point quelconque de la surface.
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
I
) Aire d’une sphère
(ou surface sphérique ): L’aire d’une surface sphérique est égale au produit de la longueur de la circonférence d’un grand
cercle par le diamètre . On
dit aussi : l’aire d’une surface sphérique est égale à 4 fois le produit
de « pi » par le carré du rayon
Soit
A = 2pr On
dit encore que l’aire est proportionnelle au carré du rayon. Elle
vaut quatre fois l’aire d’un grand
cercle. Application :
Calculer l’aire d’une sphère de 0,5 m de rayon résolution A =
0,5 A =
3,1416 m2 |
|
|||||||||||||||
|
|
Dont : Aires de parties remarquables ( fuseau et zone
sphérique et calotte sphérique) : |
|
|||||||||||||||
|
|
Fuseau :
(« a » lire
« alpha ») |
|
|||||||||||||||
|
|
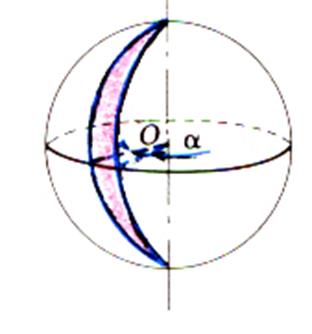
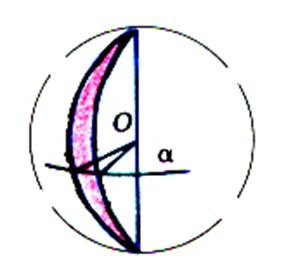
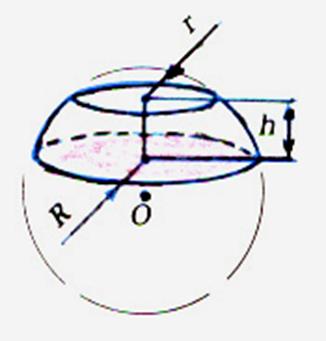
Le fuseau est la partie de sphère limitée par deux demi- grands cercles de même extrémités : L’aire est : A = 2a R² Où « a »
désigne l’angle des demi – plans ( en
radians) L’aire est proportionnelle à
l’angle ; si a = 2p ,
on retrouve l’aire de la sphère.
|
|
|||||||||||||||
|
|
Zone
sphérique : |
|
|||||||||||||||
|
|
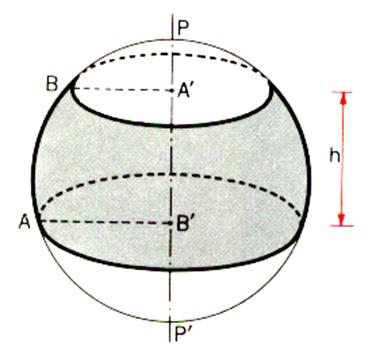
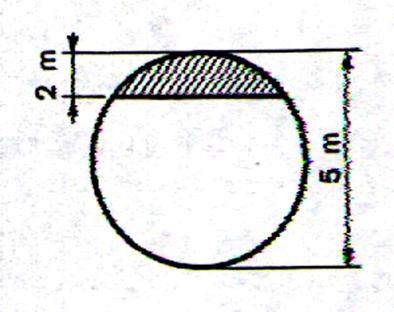
Une zone sphérique est la partie d’une sphère comprise entre deux plans parallèles .Si l’un des plans est tangent à la sphère , la zone porte le nom de « calotte sphérique ». L’aire A de la zone limitée par des plans à la distance
« h » est : A = 2pRh |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
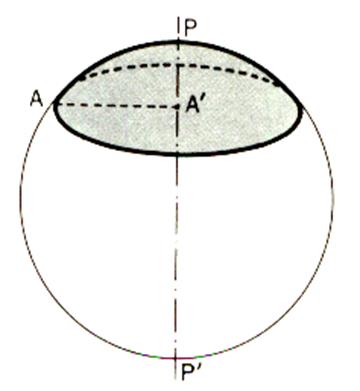
Calotte sphérique : |
|
|||||||||||||||
|
|
La calotte est l’une des deux
parties de la sphère découpées par un cercle . A = 2pRh Cette formule se retient facilement : c’est l’aire du cylindre de
rayon « R » et de hauteur « h ».
|
|
|||||||||||||||
|
|
INFO :
Sur la terre , la zone comprise entre deux
tropiques est la zone torride . Les calottes limitées par les cercles
polaires sont les calottes glaciaires . les zones
limités par un tropique et un cercle
polaire d’un même hémisphère sont les zones tempérées . |
|
|||||||||||||||
|
|
II
) VOLUME de
la SPHERE ( ou boule) : (ici : Calcul du volume d’une sphère par intégration.) |
|
|||||||||||||||
|
|
VOLUME de la boule (SPHERE) : le volume est proportionnel au cube du rayon. |
|
|||||||||||||||
|
|
Le volume de la sphère est égale au tiers du
produit de son aire par le rayon : V = Soit
V = ou ( r = R )
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Application : 1°)Calculer le volume d’une sphère de 0,50m
de rayon : Résolution : on sait que V = 2°) calculer le rayon d’une sphère dont le volume est 200 cm3 200 = 3 log R = lg 150 + log 3log R = 1,67894 log R = |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Autres exercices résolus : |
|
|||||||||||||||
|
|
1
) Déterminer le volume d’une sphère |
|
|||||||||||||||
|
|
·
Calcul de « V » , en centimètres
cubes , pour R = 12 cm
·
Calcul de « V » , en centimètres
cubes , pour R = 2 m
|
|
|||||||||||||||
|
|
2 ) Déterminer le volume d’une sphère |
|
|||||||||||||||
|
|
·
Calcul de « V » , en centimètres
cubes , pour R = 2,5 cm
·
Calcul de « V » , en centimètres
cubes , pour R = 0,15 cm
V |
|
|||||||||||||||
|
|
3 ) Déterminer le volume d’une sphère |
|
|||||||||||||||
|
|
·
Calcul de « V » , en mètres cubes ,
pour R = 31 m
V ·
Calcul de « V » , en mètres cubes ,
pour R = 1,45 m
V |
|
|||||||||||||||
|
|
4 ) Déterminer le volume d’une sphère |
|
|||||||||||||||
|
|
V V |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Volumes de parties remarquables : (revu le 30/5/2012) |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Onglet |
|
|||||||||||||||
|
|
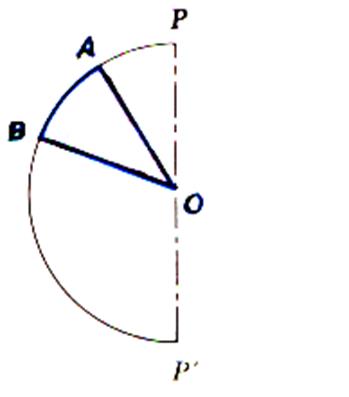
L’onglet est le solide limité par la sphère et deux demi – plans
passant par un même diamètre . Le volume est Où « a » désigne
l’angle des demi – plans ( en radians) Nota : si « a = 2p » , on retrouve le
volume de la sphère. |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Secteurs
sphériques |
|
|||||||||||||||
|
|
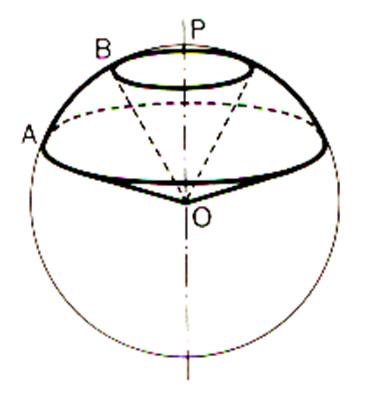
Le secteur sphérique est le solide engendré par
un secteur circulaire tournant autour d’un diamètre qui ne le traverse pas .
|
|
|||||||||||||||
|
|
Le volume du secteur sphérique est le tiers du produit
de la zone qui le limite par le
rayon de la sphère. Lorsque « h = 2R »,
on retrouve le volume de la sphère. |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Segment
sphérique (à une base) |
|
|||||||||||||||
|
|
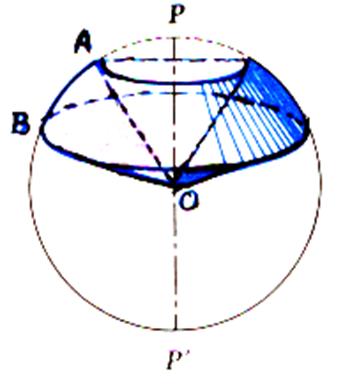
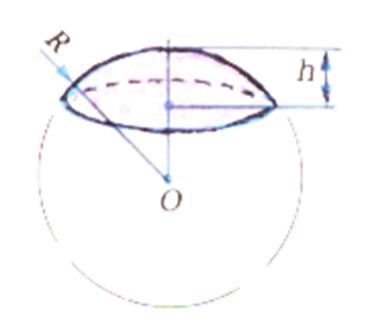
Le volume du segment sphérique à une base
est : Si l’on
remplace « h » par
« 2R » , on retrouve le volume de la
sphère. |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Segment
sphérique ( à deux bases) |
|
|||||||||||||||
|
|
Le segment sphérique à deux bases est le solide limité par la sphère et deux
plans parallèles. C’est donc la partie de l’espace limitée par un zone et deux disques. En appelant
« h » la distance entre les deux plans, « R » et
« r » les rayons des sections : Le volume du segment sphérique à deux bases s’en
déduit par différence. Soit On obtiendra
ce résultat par différence des volumes entre les deux calottes de rayon
« R » et « r » ;
avec ( R > r ) |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Lorsque « r
= 0 » , on retrouve le volume de la
calotte sphérique. L'aire de la zone
sphérique correspondante est « |
|
|||||||||||||||
|
|
(pré
requis : les puissances de dix)
Pour information La masse
de la terre = 5,977 La masse de la lune = 7,352 La masse du soleil = 1,989 |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
TRAVAUX AUTO FORMATIFS. |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
1°) a quoi est égale l’aire d’une sphère ?
donner la formule ! 2°) a quoi est égale le volume d’une
sphère ? donner la formule ! EVALUATION
1°) : Calculer l’aire d’une sphère de 0,5 m
de rayon 2 °) Calculer le volume d’une sphère de
0,50m de rayon : 3° ) Une sphère à un
rayon de 70 mm quelle est son volume ? 4°)
5°)
6°)
7°)
Problèmes : a) Calculer le volume de gaz nécessaire pour
gonfler un ballon sphérique de 18 m de diamètre . b) Un
ballon sphérique a une contenance de 3,5 litres lorsqu’il est rempli jusqu’à
la naissance du col. Quel est le rayon de ce ballon ? c ) Une bille
sphérique à un diamètre de 75 mm . Quelle est sa masse , la masse volumique du fer étant
7,8 g/cm3 d)
e)
INTERDISCIPLINARITE
1° ) Quelle est l’aire de la surface
d’un ballon sphérique qui a 10m de diamètre ? 2° ) Une tour ronde de 15,70 m de circonférence est surmonté d’une coupole. Trouver l’ aire de la surface de cette coupole. 3°) Une boule de pétanque à un diamètre de 70 mm quelle est son volume ?
Quelle est sa masse sachant qu’elle est en acier ? (masse
volumique du fer 7,8 kg.dm-3)
Quelle est sa masse sachant qu’elle est en cuivre
? (masse volumique du fer 8,8 kg.dm-3) 4°) Un vase cylindrique de 7 ,4 cm de rayon
et 0,24 m de hauteur est plein d’eau . On y plonge
une bille de billard de 84 mm de diamètre . Combien
reste – t- il de centilitres d’eau dans le vase ? 5°) Dans l’un des plateaux d’une balance , on met une boule de fer de 2cm de rayon , et
dans l’autre , une boule en ivoire de 10 cm de diamètre. De quel côté penchera la balance et quel
poids faudra-t-il ajouter de l’autre
côté pour rétablir l’équilibre ? La
densité du fer est de 7,8 et celle de l’ivoire 3,8 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||