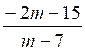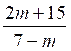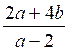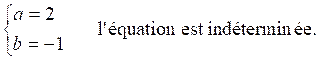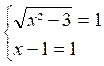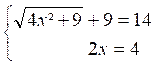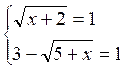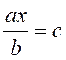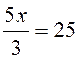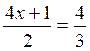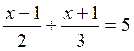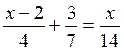Pré requis:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Environnement du dossier :
DOSSIER (suite): Forme générale de
Résolution d'une
équation du premier degré à une inconnue
I ) EQUATIONS DU PREMIER DEGRE A UNE INCONNUE.
II) « Equation paramétrée ». ( 3 exemples)
III )
Equations à une inconnue dont la résolution se ramène a celle d’équations du
premier degré.
IV )
Equations qui renferment des dénominateurs contenant l’inconnue.
|
|
COURS |
Devoir Contrôle |
Interdisciplinarité |
|
COURS
I ) EQUATIONS DU PREMIER DEGRE A UNE
INCONNUE.
EQUATION ENTIERE :
En faisant
passer tous les termes dans un même membre , toute
équation peut se mettre sous la
forme P = O
Si P
est un polynôme, on dit que l’équation est « entière » et le degré
est le degré de l’équation.
|
Ainsi 3 x3 + 5 x² - 4x + 3 = 3 x ( x² - 4x) + 5 est une équation du second degré parce
qu’elle est équivalente à : 17 x² - 4 x - 2 = 0 |
Transformations
successives : 3 x3
+ 5 x² - 4x + 3 = 3 x ( x² - 4x) + 5 3 x3
+ 5 x² - 4x + 3 = 3 x3 - 12 x²
+ 5 3 x3
+ 5 x² - 4x + 3 - 3 x3 + 12 x² -15
= 0 17 x²
- 4 x - 2 = 0 |
EQUATION DU PREMIER DEGRE. D’après ce qui précède , une équation du premier degré est une équation de
la forme
P = 0
P étant un polynôme du premier degré.
Si l’on fait
passer tous les termes contenant l’inconnue « x » dans le premier membre
et tous les autres dans le second, on obtient une équation de la forme.
(1)
a x = b
« a » et « b »
étant des données.
1°) si a ¹ 0 , on peut diviser les deux membres par
« a ».On voit ainsi que l’équation (1) admet une seule solution :
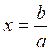
2°)Si a = 0 l’équation (1) s ‘écrit : 0 × x = b
Or quel que
soit « x », le premier membre est nul . Donc
si « b » est différent de zéro, l’équation n’admet aucune solution.
On dit qu’elle est impossible.
Si
« b » est nul, quel que soit « x », l’équation est toujours
satisfaite. On dit qu’elle est indéterminée.
En
résumé :
si a ¹ 0 solution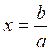
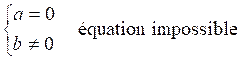
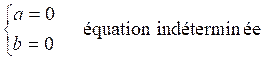
REMARQUE :
Si l’équation renferme des données littérales ( paramètres),on
sera en général amené à distinguer plusieurs cas car pour certaines valeurs des
paramètres le coefficient de l’inconnue pourra être nul et on n’aura pas le
droit de diviser les deux membres de
l’équation par ce coefficient.
Exemple 1 : résoudre l’équation :
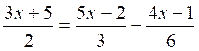
Chassons les dénominateurs. On obtient :
3 ( 3x+5) = 2
( 5x -2) - (4x -1)
9X +15 =
10 x - 4 - 4x +1
9x +15 =
6x -3
3x
= -18
x = - 6
II ) Equation paramétrée :
« Résoudre l’équation » :
Exemple 1
|
|
m (x+2) +
2x =
3 ( 3x -5) dans laquelle « x » est l’inconnue et
« m » est un paramètre. L’équation est équivalente à : m x + 2 m + 2x =
9x -15 m x + 2x
- 9x = - 2m - 15 (m-7)x = -2 m -15 1°) si m ¹ 7 alors x
= 2°) Si m
= 7 l’équation
s’écrit :
0 × x = -29 elle est donc impossible. |
|
Exemple
2
Résoudre et discuter suivant les valeurs du paramètre « m »
représentant un nombre connu, l’équation : 2 ( m - 1)x - m (
x-1) = 2m +3
Développons et réduisons les termes
semblables :
2 m x - 2x - m x + m = 2m + 3
m x - 2x = m
+3
a) si m - 2 ¹ 0 ou m ¹2 , alors l’équation admet la
solution unique :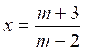 
b) si m-2 = 0 ou m=2 ,
l’équation se réduit à 0x = 5
L’équation n’admet pas de solution.
Exemple III (à 2 paramètres) Résoudre
l’équation a (x-2) + 2x = 4 ( x
+b)
|
|
( « x » est l’inconnue et
« a » et « b » deux paramètres. L’équation est équivalente à : a x
- 2a +2x = 4x + 4b a
x +2x - 4x = 2a + 4b
( a -2) x
= 2 a + 4 b 1°) Si a ¹
2 ; x = 2°) Si a = 2
l’équation s’écrit : 0 × x = 4 + 4b Donc si 4 +
4b ¹ 0
c’est à dire si b ¹ -1 l’équation est impossible. Si b = -1 l’équation
est indéterminée. En
résumé : Si a ¹0 : 1
solution ; x = Si Si |
|
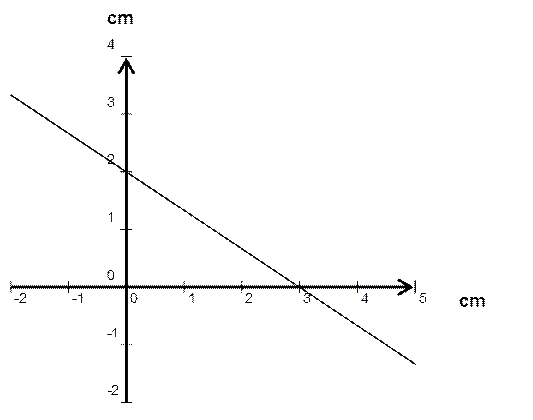
APPLICATION : construction du graphique d’une fonction affine (@ ). Nous avons
vu que pour construire le graphique d’une fonction affine « y = ax+b » on en construisait deux points. Souvent on
prend les points de rencontre avec les axes de coordonnées. Le point de
rencontre avec l’axe des « y » s’obtient, comme nous l’avons vu, en
faisant « x = 0 », ce qui donne « y = b »
Le point de rencontre avec l’axe des « x »
est le point du graphique pour lequel ona
« y=0 »
On l’obtiendra donc en résolvant l’équation « a
x + b = 0 »
Ce qui donne
x = 
Ainsi , on a construit ci-contre le
graphique de la fonction y =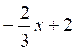 
|
|
De même, pour préciser le tracé du graphique d’une fonction homographique (@ )
y =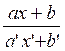 
on pourra chercher le
point de ce graphique qui est sur l’axe des « x ». Pour ce point on a
« y = 0 » , donc a x+b = 0 c’est à dire x =
III ) Equations à une inconnue dont la résolution se ramène a
celle d’équations du premier degré.
Equations entières . Il est souvent possible de résoudre
une équation entière qui n’est pas du premier degré en procédant ainsi :
1°) On fait passer tous les termes dans un même membre. On obtient
ainsi une équation de la forme :
(1)
P = 0
« P » est un polynôme.
2°) On essaie de mettre « P » sous la forme d’un produit de facteurs
du premier degré.
Par exemple , si P est le
produit de trois facteurs du premier
degré A ; B ;
C ;l’équation (1) s’écrit :
(2)
A × B × C = 0
Résoudre cette équation, c’est déterminer les
valeurs de l’inconnue pour lesquelles le produit A × B × C
est nul. Pour cela, il faut et il suffit que l’un des facteurs du produit soit nul
, c’est à dire que l’on ait :
A = 0 ;
B = 0 ou C = 0
On est ainsi ramené à résoudre trois équations du premier
degré à une inconnue.
Exemple :
Résoudre l’équation : ( 9x + 12 ) ( 2 x² -8) = ( 9 x + 12 )
( 4x + 8 )²
Cette équation s’écrit :
( 9x + 12 ) ( 2
x² -8) - ( 9 x + 12 ) ( 4x + 8 )² = 0
6 ( 3x +4) ( x -2) ( x +2)
- 48 ( 3x +4) ( x +2 ) ² = 0
( 3x +4 ) ( x
+2) [ ( x -2) - 8 ( x +2) ] = 0
( 3x +4 ) ( x
+2) ( x - 2 - 8x - 16 ) = 0
( 3x +4 ) ( x
+2) ( - 7x - 18
) = 0
Cette équation se décompose en trois :
3x +4 = 0
x + 2
= 0
et
- 7x - 18 = 0
Elle admet donc 3 racines :
x = 
; x = - 2 et
x = 
IV
)
Equation contenant l’inconnue au dénominateur :
Si on fait passer tous les termes dans un même
membre on obtiendra , après réduction au même
dénominateur, une équation de la forme :
(1) 
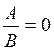
Les racines de cette équation sont celles de l’ équation A = 0 qui n’annulent pas B .
On saura donc résoudre les équations de cette forme
si « A » est un polynôme que l’on peut mettre sous la forme d’un
produit de facteurs du premier degré.
Exemple n°1
Résoudre l’équation
(1) 
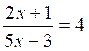
Cette équation est équivalente à :
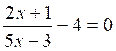
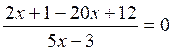
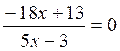
Le
numérateur s’annule pour « x » = 
. Cette valeur n’annule
pas le dénominateur, donc elle est racine de l’équation (1).
L’équation n’a de sens que si le
dénominateur est différent de zéro, c’est à dire si x ¹ 
Exemple n°2 : Résoudre l’équation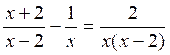 
L’équation n’a de sens que si les dénominateurs sont différents de zéro, c’est
à dire si x ¹ 0 et x ¹ 2 . Supposons
ces conditions réalisées, nous pouvons supprimer les dénominateurs en
multipliant tous les termes par x (x-2).
x
(x-2). - ( x - 2) = 2
x²
+ 2x - x + 2 = 2
soit : x² + x = 0 ou x ( x +1) = 0
ces équations se décompose en deux
autres :
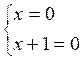d’
où les racines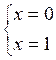 
La valeur x= 0
est une des valeurs exclues. Seule x = - 1 est racine de l’équation proposée .
La méthode générale qui en découle est
donc la suivante :
Pour résoudre une équation contenant l’inconnue au
dénominateur :
On cherche une équation équivalente en supprimant
les dénominateurs et on résout l’équation entière obtenue. On écarte parmi les
racines trouvées, celles qui annulent un des dénominateurs de l’équation
réduite.
Exercice n°3 : Résoudre l’équation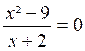 
la fraction du premier membre n’est définie que si
son dénominateur x + 2 est différent
de zéro , donc si x ¹ -2 . Cette condition étant
réalisée, la fraction est nulle si et seulement si son numérateur est nul.
D’où : x ² -9 = 0 Û ( x +3)( x - 3) = 0
les solutions de cette équation sont
x= -3 et x= +3. Ces deux valeurs étant différentes de -2 ,
sont racines de l’équation proposée.
|
|
||
|
|
|
|
|
|
Définition : une équation irrationnelle est une équation qui renferme
un ou plusieurs radicaux portant sur des
expressions contenant l’inconnue. Dans le cas contraire, l’équation est
dite « rationnelle ». Nous allons voir que la résolution de
certaines équations irrationnelles se ramène à celle d’équations du premier
degré. Exemple 1 : résoudre
l’équation (1) S’il existe une valeur de
« x » pour laquelle les deux membres de cette équation sont égaux,
pour cette valeur les carrés des deux membres sont aussi égaux. Donc toute racine de l’équation (1)
est racine de l’équation : x² -
3 = ( x - 1)² Cette équation s’écrit : x
² - 3 = x² - 2x +1 2 x = 4 x
= 2
x = 2 est donc la seule solution possible de l’équation (1) Pour voir si cette valeur est
effectivement racine de l’équation (1), il suffit de vérifier. Pour
x = 2 , on a :
x = 2 est donc bien racine
de l’équation (1) Exemple 2 : Résoudre l’équation (1)
S’il existe une valeur de
« x » pour laquelle les deux membres de cette équation sont égaux, cette
valeur satisfait aux équations suivantes :
4
x² +9 = (2x -9 )² 4
x² +9 = 4x² - 36 x + 81
36 x =
72
x = 2
x = 2 est donc la seule solution
possible de l’équation(1) . Vérifions : Pour
x = 2 , on a :
x = 2 n’est donc par racine de l’équation (1) et celle-ci n’admet aucune
solution. Exemple 3 : Résoudre
l’équation : (1) S’il existe une valeur de
« x » pour laquelle les deux membres de cette équation sont égaux,
cette valeur satisfait aux équations : x + 2
= 9 - 6
6 5 + x = 4 x = -1 Donc l’équation (1) a une seule racine
« possible » : x = -1 Pour voir si cette valeur est
effectivement racine de l’équation (1), vérifions. Pour « x » = -1 , on a
donc x = -1 est bien racine de l’équation (1) |
|
|
|
|
|
|
|
Info +++ ► |
Pour chaque cas « cliquer sur «
»
|
Equation type: ax = b
; 9 x = 45 |
Savoir résoudre |
Electricité
|
|
|
Physique : |
|
|
Mécanique (poids et masse) |
|
|
Mouvement uniforme |
|
|
Travail d'une force |
|
|
Mouvement uniformément varié |
|
|
Equation type ax -b =
c ; 5x -14 =16 |
Savoir résoudre |
|
Surface d'un triangle |
|
|
Calcul d'intérêt simple |
|
|
Densité d'un corps |
|
|
Equation
type |
|
|
Equilibre d'un levier |
|
|
Roues et engrenages |
|
|
Equilibre d'un treuil |
|
|
Chimie : |
|
Chimie :
L’atome : On donne l’écriture suivante : 1123
Na (qui symbolise l’atome de Sodium (natrium)), combien compte t- on de
neutrons ?
TRAVAUX AUTO
FORMATIFS.
-
Donner la procédure pour résoudre une équation du
premier degré , comportant des parenthèses et des
dénominateurs.
-
Devoir L ( le corrigé est dans le cours
précédent)
PARTIE I :
Série 1 :
|
|
Résoudre : |
Résolution |
|
1-a |
4,6 x = 18,4 |
|
|
1-b |
|
|
|
1-c |
4 ( x -3) = 2 ( x-5)+3 |
|
|
1-d |
|
|
Série 2 :
|
|
Résoudre : |
Résolution |
|
1-a |
9x = 4,2 |
|
|
1-b |
7 x + 3,2 = 7,7 |
|
|
1-c |
3 ( 2x - 1) = 5 ( 6x + 4,2) |
|
|
1-d |
|
|
PARTIE II
1°) Résoudre l’équation :
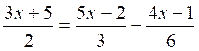
2°) Résoudre
l’équation :
( 9x + 12 ) ( 2 x² -8) = ( 9 x + 12 ) ( 4x + 8
)²
3°)
Résoudre l’équation
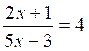
4°) Résoudre l’équation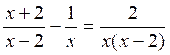
N°4 Résoudre
l’équation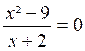
N°5 : résoudre l’équation 
N°6 Résoudre l’équation 
N° 7 Résoudre l’équation : 
PARTIE III : Niveau +++(sur les
équations paramétrées)
1°) Résoudre
l’équation et discuter : m
(x+2) + 2x = 3 ( 3x -5)
2°) Résoudre et discuter suivant les
valeurs du paramètre « m » représentant un nombre connu,
l’équation : 2 ( m - 1)x - m ( x-1) = 2m +3
3°) Résoudre l’équation et discuter
: a (x-2) + 2x = 4 ( x +b)