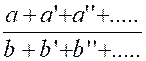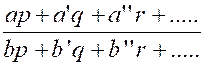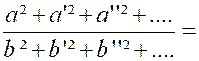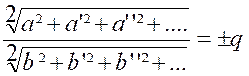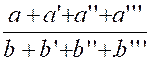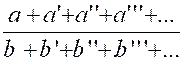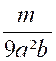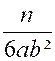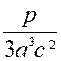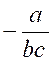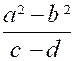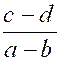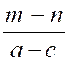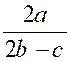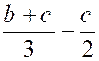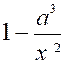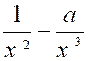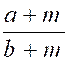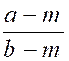Pré requis
|
|
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier :
|
Objectif
précédent : |
Objectif suivant : |
|
||
|
INFORMATIONS : Module : calcul algébrique
|
||||
LES
CALCULS FRACTIONNAIRES : FRACTIONS
algébriques : EGALES et INEGALES .
· Les suites de fractions égales .
· Les suites de fractions
inégales.
· Complément :
« moyenne arithmétique »
|
|
|
|
|
||||
|
TEST |
COURS
|
|
|||||
|
|
|
|
|
Les
suites de fractions égales . |
|
|
|
|
|
|
|
|
Théorème :
Etant donnée une suite de fractions égales , on
obtient une fraction égale à chacune d’elles en divisant la somme algébrique
des numérateurs par la somme algébrique des dénominateurs. Démonstration : Soient
les fractions égales : « En
additionnant ces égalités membre à membre , il vient : «
a + a’+ a’’ + ….= bq + b’ q + b’’q +
…. » «
a + a’+ a’’ + ….= q ( b + b’ + b’’+ ….) » et en divisant de par
et d’autre par (
b + b’ + b’’+ …. ) on obtient :
« Corollaires : Corollaire N°1 : On peut , avant
d’additionner les fractions terme à terme , multiplier les deux termes de
chaque fraction par un même facteur arbitraire.. En
effet ;on a
« Corollaire N°2: On peut ajouter certaines fractions
terme à terme et retrancher terme à terme certaines autres. En
effet , si , dans la suite proposée , on remplace,
par exemple ,la fraction « Corollaire N°3: On obtient une fraction égale, en
valeur absolue, à chacune des fractions
proposées en divisant la racine carrée de la somme des carrés des
numérateurs par la racine carrée de la somme des carrés des dénominateurs. En
effet , en ajoutant membre à membre les
égalités « a = bq ; a’
= b’ q ; a’’ = b’’q ; …. » préalablement élevées au carré on
a : « a² + a’² +
a’’² + ….= b²q² + b’² q² + b’’² q² + ….. » d’ où « et , en prenant la
racine des deux membres :
|
|
|
Les
suites de fractions inégales . |
|
|
|
Etant
donnée une suite de factions inégales à dénominateurs tous positifs ou tous
négatifs, la fraction obtenue en divisant la somme des numérateur
par la somme des dénominateurs est comprise entre la plus grande et la plus
petite d’entre elles. Soit
la série décroissante : « D’où
si les dénominateurs sont positifs
On a «
a = b h » ; « a’
< b’ h » ; « a’’ < b’ h » ; « a ‘’’ < b’’’ h » d’où : « a + a’+ a’’ + a ‘’’ < h
( b + b’ + b’’+ b ‘’’ )
» ou enfin : «
Appelant
« k » la plus petite , Donc : « Si
les dénominateurs sont tous négatifs , On a «
a = b h » ; « a’
> b’ h » ; « a’’ > b’ h » ; « a ‘’’ > b’’’ h » d’où : « a +
a’+ a’’ + a ‘’’+ …. > h ( b
+ b’ + b’’+ b ‘’’+ … ) » ou enfin : «
Il vient de même : « Complément :
Calcul de la moyenne « arithmétique » : (info +++) Une quantité « q » est dite
« moyenne » entre plusieurs quantités « a ; b ;
c ; .. » lorsqu’elle n’est
ni supérieure à la plus grande de ses quantités , ni
inférieure à la plus petite , et cette propriété s’exprime par la notation
« q = Moy.( a ; b ; c ;..) Ainsi , quelles que soient
les fractions à dénominateurs de mêmes signes : « La
somme de plusieurs quantités , ainsi divisée par le
nombre de ces quantités , porte le nom de « moyenne arithmétique »
, ou parfois , simplement de « moyenne » |
|
|
|
|
|
|