|
Aller vers lire….la numération , ne pas
confondre : « nombre » et « grandeur » |
Pré requis:
|
|
|
|
Nomenclature |
|
|
Division de N par 10 ; 100 ;1000 |
ENVIRONNEMENT du dossier:
|
|
|
|
COURS FICHE collège 6ème / 5ème |
|
Objectif précédent : |
1°) Numération des nombres décimaux. 2°) Classification des nombres décimaux 3°) Propriétés
des opérations Net D. |
Classe 6ème –cinquième- collège :
Corrigé
CALCULS SUR LES NOMBRES DECIMAUX
|
|
Chapitres : |
|
|||||
|
|
1°) Les décimaux –les entiers naturels.
(reconnaître ; classification) |
|
|||||
|
|
2°) Valeur approchée. (
troncature, arrondi ;….) |
|
|||||
|
|
3°) Addition (propriétés ;
ordre de grandeur ;….) |
|
|||||
|
|
4°) Soustraction. |
|
|||||
|
|
5°) La multiplication.
(Propriétés de la multiplication ; ordre de grandeur d’un produit ….). |
|
|||||
|
6°) Produit d’un produit par un nombre. |
|
||||||
|
|
|
||||||
|
|
|
||||||
|
|
·
Simplification de l’
écriture d’une suite de calculs par
suppression de parenthèses ou crochets. |
|
|||||
|
|
|
|
|||||
|
|
|||||||
|
TEST |
COURS |
Interdisciplinarité Devoirs |
|
||||
|
|
|
|
|
>>> Liste de fiches de travaux |
|
|
|
COURS
Ceci est le résumé d’un cours dispensé au collège.
Cliquer sur les « info + » ; « pré requis » ,…….. pour
avoir des précisions ou pour approfondir..
|
Info + |
1°) Les décimaux – les entiers naturels. |
|
||||||||||||
|
|
Exemples : soit une suite de nombres
décimaux : 37,15 ; 0,63 ;
0,0003 ; 7,00 ;………….. |
|
||||||||||||
|
|
Dans le nombre décimal : « 37,15 » : « 37 »
est appelé :la partie entière et
« 15 »
la partie décimale. |
|
||||||||||||
|
Remarque
1 : On
obtient une autre écriture d’un décimal en mettant des zéros à la droite de
la partie décimale : Ainsi : « 37,15 » ;
« 37,150 » ; « 37,1500 » ; « 37,15000 » :sont quatre écritures d’un même
décimal. |
|
|||||||||||||
|
|
Remarque
2 : De
la même façon le nombre « 37 »
peut s’écrire : « 37,0 » ;
« 37,00 » ;
« 37,0000 »
ou ………………. Nous avons vu que « 37 » est un entier
naturel ; il peut être considéré comme étant un nombre décimal. ( sa partie décimale n’est faîte que de
« 0 ») |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Remarque
3 : Au lieu
de dire « entier naturel » , on dit souvent « entier » ou
parfois « naturel » |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Exercices série
1 : Exemple : On vous donne un extrait de la
liste des entiers naturels .
« 0 ; 1 ; 2 ; 3 ; 4 » est la liste des entiers naturels « x »
tels que « x |
|
||||||||||||
|
|
On vous demande : |
|
||||||||||||
|
|
Ecrire la liste des entiers naturels « y » tels que :
y < 5 |
………………………………………………. |
|
|||||||||||
|
Ecrire la liste des entiers naturels « z » tels que :
2 |
………………………………………………. |
|||||||||||||
|
Ecrire la liste des entiers naturels « t » tels que 6 <
t |
………………………………………………. |
|||||||||||||
|
Ecrire la liste des entiers naturels « u » tels que 9 |
………………………………………………. |
|||||||||||||
|
Ecrire la liste des entiers naturels « v » tels que 3 <
v < 10 |
………………………………………………. |
|||||||||||||
|
|
|
|
||||||||||||
|
Exercice 2 :
On vous demande de ranger dans l’ordre croissant ( symbole à utiliser : ….< …..) |
||||||||||||||
|
|
42,57 ; 0,13 ;
0,0069 ; 47,4 ; 7 ; 0 ,1 ; ; 47,31 ;
0,0071 ; 42 , 428 ; 0,2 |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
2°) Valeur approchée. |
|
||||||||||||
|
|
Voici un encadrement de « 537, 268 »
par des entiers consécutifs :
« 537 < 537,
268 < 538 » On dit que : « 537 » est la valeur
approchée à 1 prés par défaut de
« 537, 268 » On dit que : « 538 » est la valeur
approchée à 1 prés par excès de « 537, 268 » On dit que : « 530 »
est la valeur approchée à 10 prés par défaut de « 537, 268 » On dit que : « 540 »
est la valeur approchée à 10 prés par excès
de « 537, 268 » On
écrira : « 530 < 537,
268 < 540 » à 10 prés . Encadrement de « 537, 268 » à 100
prés : On écrira :
« 500 <
537, 268 < 600 »
à 100 prés . Encadrement de « 537, 268 » à 0,1
prés : On écrira :
« 537,2 <
537, 268 < 537,3 » à
0,1 prés . Encadrement de « 537, 268 » à 0,01
prés : On écrira :
« 537,2 6 <
537, 268 < 537,27 » à
0,1 prés . |
|
||||||||||||
|
|
Vocabulaire :
|
|
||||||||||||
|
|
« Troncature » :
Les valeurs approchées par défaut sont aussi appelées « troncature » Exemples
de troncatures possibles de « 537, 268 » : « 537 » ; « 537,
2 » ; « 537, 26 » |
|
||||||||||||
|
|
« arrondi
» : Des deux valeurs
approchées par excès ou par défaut , celle qui est la plus proche du nombre
est appelée « arrondi » |
|
||||||||||||
|
|
Exemples
« d’arrondi » de « 537,
268 » : « 500 » : « 540 » ;
« 537 » ; « 537,3 » , « 537,26 » |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|||||||||||||
|
|
|
|
||||||||||||
|
|
« ordre
de grandeur » Un ordre de grandeur est une valeur approchée. Mais très souvent , on choisit pour ordre de
grandeur d’un nombre , un arrondi dans lequel tous les chiffres sont nuls
sauf un. Exemples :
pour « 537, 268 » on prendra « 500 » comme ordre
de grandeur. Pour « 3,8 » on prendra « 4 » . Pour
« 0,0062 » on prendra « 0,006 » |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
On vous demande donner une troncature avec deux chiffres après la
virgule de « 81 , 5372 »
est égale : « 81 ,
53 » Mais
remarquez bien la valeur de la troisième décimale : On vous demande donner arrondir avec deux chiffres après la virgule de
« 81 , 5372 » est
égale : « 81 , 54 » On vous demande donner arrondir avec deux chiffres après la virgule de
« 81 , 5342 » est
égale : « 81 , 53 » On vous demande donner arrondir avec deux chiffres après la virgule de
« 81 , 535 » est
égale : « 81 , 54 » On remarque qu’il existe une règle à
respecter !!! voir le cours suivant la règle de l’arrondi « à tant
prés ». On vous demande un arrondi à la dizaine prés de
« 157,41 » est « 160 » |
|
||||||||||||
|
|
|
|
||||||||||||
|
A revoir |
3°) Addition : |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
||||||||||||||
|
|
1°) Elle est commutative 2°) Il existe un élément neutre qui est
« 0 » 3°) Elle est associative. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Exercices
. Calculez le plus rapidement possible après avoir regroupé
les termes de telle sorte qu’il apparaisse des dizaines. ( exemple : 28 + 62 = 90) |
|
||||||||||||
|
|
A = 21 + 17 + 84 + 72 + 53 + 39 + 46 |
|
||||||||||||
|
|
A = ( ……+
…….) + ( ……+ …….) +( ……+ …….) + ……… A = ………………+ ……………….+ ………………..+ ……………. A = ……………………. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Ordre d’une grandeur d’une somme. |
|
||||||||||||
|
|
Considérons la somme « 37, 432 +
524 ,37 » Un ordre de grandeur de « 37, 432 »
est «40 » , un ordre de
grandeur de
« 524 ,37 » est « 520 ». Un ordre de grandeur de la somme est alors
« 40 + 520 = 560 » Contrôle en faisant le calcul « 37,
432 +
524 ,37 = » Faîtes de même en complétant le tableau
ci-dessous : |
|
||||||||||||
|
|
Nombre
à additionner |
Calcul
d’un ordre de grandeur |
Résultat
exact. |
|
||||||||||
|
72,438
+ 578,61 |
|
|
||||||||||||
|
0,00432 + 0,00067 |
|
|
||||||||||||
|
126837 + 73 842 |
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
4°) Soustraction. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
A
retenir : |
|
||||||||||||
|
|
« a » et « b » étant des
décimaux positifs quelconques , le calcul
de « a – b » n’est possible
que si « a > b » |
« a
– b = x » signifie que « a = x + b » |
|
|||||||||||
|
|
|
|
||||||||||||
|
Après avoir fait des essais ( au brouillon) , dites ( en répondant par
« oui » ou « non » ) si , dans l’ensemble des décimaux ,
la soustraction est commutative ( …non …..) associative ( …non…)
|
|
|||||||||||||
|
|
|
|
||||||||||||
|
Exercice
, Série 1 .Heure , minute,
seconde, sont représentées respectivement par « h » ,
« min » , « s » Calculez (
faire les réductions sachant que
« 1 h = 60 min = 60 ‘ ) et « 1 min = 60 s = 60
‘’ » : |
|
|||||||||||||
|
|
5 h 38 min 54 s
+ 8 h 47 min 23 s = |
|
|
|
||||||||||
|
13 h 45 min 37 s
- 5 h 29 min 18 s = |
|
|
||||||||||||
|
18 h 14
min 21 s - 7 h 34 min 45 s = |
|
|
||||||||||||
|
|
|
|
||||||||||||
|
Exercice
, Série 2 Compléter le tableau donnant les horaires des
trains sur le trajet : Marseille - Paris. |
|
|||||||||||||
|
|
|
Départ de Marseille |
Arrivée à Paris |
Durée du trajet. |
|
|
||||||||
|
|
16
h 56 min |
23
h 7 min = 22 h 67min |
22h 67 – 16 h 56min= 6 h 11 min |
|
||||||||||
|
|
21
h 52 min |
6
h 29 min |
|
|
||||||||||
|
|
20
h 17 min |
|
8
h 23 min |
|
||||||||||
|
|
|
7
h 14 min |
7
h 58 min |
|
||||||||||
|
|
Info :
23 h 7 min =
22 h + 1 h +7min = 22 h
+ 60 min +7min = 22 h 67 min |
|
||||||||||||
|
|
5°) La multiplication. |
|
||||||||||||
|
|
|
|
||||||||||||
|
Exercice
1 : |
|
|||||||||||||
|
|
On sait que
« 43 |
|
||||||||||||
|
|
« 43
|
43
|
« 4,3
|
|
||||||||||
|
« 4,3
|
« 0,
43 |
«0, 43
|
||||||||||||
|
« 0,
043 |
« 43
|
« 4,3
|
||||||||||||
|
« 4300
|
« 0,
043 |
« 0,
043 |
||||||||||||
|
« 43
000 |
« 0,
000 43 |
« 43
000 |
||||||||||||
|
« 43
00 |
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Propriétés
de la multiplication. |
|
||||||||||||
|
|
1°) Elle
est commutative . 2°) Il existe un élément neutre qui est
……………………..( 1 ) 3°) Elle est associative ;……………………………… 4°) Il
existe un élément absorbant qui
est ( 0 ) .
ainsi pour tout décimal « x » ; « x multiplié par 0 = 0
» |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Exercice
2 : Calculez le plus rapidement possible après avoir groupé
les facteurs de telle sorte qu’il apparaisse des nombres tels que «
1 ; 10 ; 100 ; 1 000 ; ( exemple 4 |
|
||||||||||||
|
|
B
= 5 |
|
||||||||||||
|
|
B = ( …5…. B = ………10 … B = ………300……………………………………………….. |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
Ordre de grandeur d’un produit : |
|
|||||||||||||||
|
|
On voudrait effectuer la multiplication de « 57 , 478 par
731 , 59 » , avant d’effectuer l’opération on vous demande de
donner un ordre de grandeur du produit. Un ordre de grandeur de « 57 , 478 » est « 60 » , un ordre de grandeur de
« 731 , 59 » est « 700 » Un ordre de grandeur du produit est alors :
« 60 Contrôle :
en faisant le calcul « 57 , 478 |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Nombres à multiplier |
Calcul d’un ordre de grandeur. |
Résultat exact. |
|
|||||||||||||
|
84 , 237 |
|
|
|||||||||||||||
|
0,000 728 |
|
|
|||||||||||||||
|
41456 |
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
Exercices de conversions. |
|
||||||||||||||||
|
|
N°1
On vous demande d’exprimer en secondes « 4 h 28 min 43 s » |
|
|||||||||||||||
|
|
4 h = |
|
4 |
14 400 s |
|
|
|||||||||||
|
28 min = |
|
28 |
1720 s |
|
|||||||||||||
|
43 s = |
|
43 s = |
43 s |
|
|||||||||||||
|
« 4 h 28 min 43 s » |
|
contient |
16 163 s |
|
|||||||||||||
|
|
|
|
|||||||||||||||
|
|
N°2 :
On vous demande d’exprimer en minutes « 7 j 15 h 53 min » (
1 jour = 1 j = 24 h ) |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||
|
|
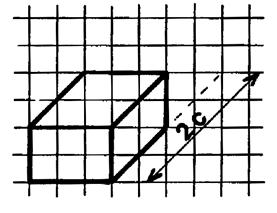
Ci
contre on vous présente un parallélépipède
rectangle ( n°1) :dont les dimensions sont : Largeur
« a » ; longueur
« b » hauteur « c ». Son volume est
égal au produit de : « a |
|
|
||||||||||||||
|
|
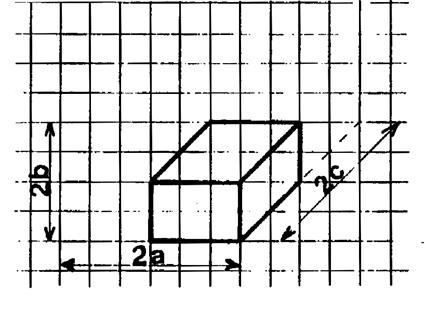
A
partir du parallélépipède « n°1 » donné ci-dessus , on vous demande
dessiner un parallélépipède «n° 2 » . Le
parallélépipède « n°2 » aura pour
dimensions les dimensions du
« n°1 » multipliés par « 2 » On
va comparer la valeur des volumes. |
|
|||||||||||||||
|
|
Indication :
|
|
|||||||||||||||
|
|
« b » et
« c » sont conservé ; « a » est multiplié par
« 2 » |
«a » et
« c » sont conservé ; « b » est multiplié par
« 2 » |
«a » et
« c » sont conservé ; « b » est multiplié par
« 2 » |
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||
|
|
Soit le volume = 2
a fois 2 b fois 2c = 2 fois 2 fois 2
fois abc. = 8
fois abc |
|
|||||||||||||||
|
|
Reprenons
le parallélépipède n°1 : Lorsque
l’on double ( multiplie par
« 2 ») les dimensions de
ce parallélépipède on obtient un autre parallélépipède contenant
8 fois ce parallélépipède. Terminez
le dessin ci contre : ( vérifier)
Si
on double les dimensions on multiplie par « 8 » pour obtenir le
nouveau volume…. |
|
|
||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Autres exemples : |
|
|||||||||||||||
|
|
|
|
On
peut écrire alors |
|
|||||||||||||
|
|
( 3 |
( 3 |
|
|
|||||||||||||
|
( 3 |
|
||||||||||||||||
|
( 3 |
|
||||||||||||||||
|
3 |
|
||||||||||||||||
|
|
Il
en serait de même pour n’importe quels nombres. On dira
alors : |
|
|||||||||||||||
|
|
Etant
donné un produit de facteurs , multiplier le produit par un nombre , revient à
multiplier l’un des facteurs par ce nombre. |
|
|
|
|||||||||||||
|
( a |
|
||||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Remarque : |
|
|||||||||||||||
|
|
Cette propriété n’est pas nouvelle . Elle découle
de la commutativité et de l’associativité de la multiplication .( voir dans
ce cours ) |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Exercice : une caisse à la
forme d’un cube de 1 mètre de côté. Combien
de boîtes cubiques de 20 cm de côté peut-on ranger dans cette
caisse ? |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Réponse 5 fois
5 fois 5 = 125 boîtes |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
||||||||||||||||
|
Soit
les calculs : |
|
||||||||||||||||
|
|
·
( 5 |
·
5 |
|
||||||||||||||
|
·
( 5 + 4 ) |
·
5 + (
4 |
||||||||||||||||
|
|
Les
nombres « 5 » ; « 4 » ; « 6 » sont
les mêmes dans les quatre cas ., mais les résultats sont différents.
Expliquez pourquoi ( oralement )
. Vous constatez
que l’ordre dans lequel on effectue les calculs est très important. |
|
|||||||||||||||
|
|
A retenir : Les parenthèses indiquent
que l’on doit effectuer en priorité les calculs figurant à l’intérieur de ces
parenthèses. |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Dans
les calculs où figurent des multiplications , on décide, pour simplifier
l’écriture , de ne plus mettre de parenthèses autour des nombres à
multiplier. |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Ainsi : |
|
|||||||||||||||
|
|
7 + ( 8
|
Le calcul
donne 7 +
8 |
|
||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Complète : ( 4
|
|
|||||||||||||||
|
|
Conséquence : si dans un calcul , il n’y a pas de
parenthèses , il faut faire attention à l’ordre dans lequel on effectue les opérations. |
|
|||||||||||||||
|
|
Ainsi : |
|
|||||||||||||||
|
|
A = 3 Signifie : A = ( 3
Le calcul donne : A = ….15 …… + 8 +
..140…… + 6 ; Le résultat A = ….169 |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
A retenir : Dans
une suite de calculs où figurent des multiplications ( ou soustraction) , mais
pas de parenthèses , on doit effectuer en priorité les multiplications. ( On
rétablit mentalement les parenthèses qui devraient figurer autour des nombres
à multiplier. On
dit que : La multiplication à priorité sur l’addition.( ou la
soustraction) |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Série d’exercices
sans parenthèses :
Calculez en appliquant la règle précédente. |
|
|||||||||||||||
|
|
B
= 6 + 3 |
B = 18 |
|
||||||||||||||
|
C
= 5 |
C = 33 |
||||||||||||||||
|
D =
9 + 4 |
D = 23 |
||||||||||||||||
|
E
= 3 |
E =
21 – 16 = 5 |
||||||||||||||||
|
F
= 6 + 5 |
F = 6 + 160 + 9 =
175 |
||||||||||||||||
|
G
= 7 + 9 |
G = 7 +
27 + 60 = 94 |
||||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Exemple d’ exercice avec
parenthèses :
Calculez en appliquant la règle précédente. |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
On
vous donne une expression à calculer
: H = 7 + 6 |
|
|||||||||||||||
|
|
On
vous demande de faire les calculs en
suivant les indications : |
|
|||||||||||||||
|
|
1°) Vous effectuez les calculs dans les parenthèses et vous réécrivez
la ligne en remplaçant le contenu des parenthèses par le nombre que vous
venez de trouver . |
|
|||||||||||||||
|
|
H = 7 + 6 |
|
|||||||||||||||
|
|
2°)
Vous réécrivez la ligne en remplaçant les nombres à multiplier par leur
produit effectué . |
|
|||||||||||||||
|
|
H = 7 + 72 + 60 + 9 |
|
|||||||||||||||
|
|
3°)
Il ne reste plus qu’à faire les additions…….et exprimer le résultat : |
|
|||||||||||||||
|
|
H = 7 + 72 + 60 + 9 |
|
|||||||||||||||
|
|
H = 148 |
|
|||||||||||||||
|
|
Faîtes
de même pour : M = 10 + (
3 |
|
|||||||||||||||
|
|
1°) M = 10 + ( 216 ) 2°) M = 10 + 648
+ 5 3°) M = 10 + 648
+ 100 4°) M = 758 |
|
|||||||||||||||
|
|
|
||||||||||||||||
|
|
|
||||||||||||||||
|
|
Rappel : ·
Dans une suite de calculs où figurent des parenthèses, on doit
effectuer en priorité les opérations indiquées à l’intérieur des parenthèses. ·
Dans une suite de calculs où ne figurent pas
des parenthèses, on doit effectuer en priorité les multiplications et
les additions (ou soustractions ) |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Série 1 d’ exercices. |
|
|||||||||||||||
|
|
Calculez
en appliquant la règle précédente : |
|
|||||||||||||||
|
|
4 |
20 + 18 = 38 |
4 + 5
|
37 |
|
||||||||||||
|
4 |
4 + 33 = 37 |
( 4 + 5
) |
81 |
||||||||||||||
|
4 |
4 |
4
+ 5 |
49 |
||||||||||||||
|
( 4 |
26 fois 3 = 78 |
( 4 + 5
) |
57 |
||||||||||||||
|
|
|
|
|||||||||||||||
|
Les crochets : […. ] Les
crochets sont des parenthèses particulières qui s’utilisent quand il y a déjà
des parenthèses à l’intérieur. Pour
effectuer une suite d’opérations où figurent
crochets et parenthèses , on calcule d’abord l’intérieur des
parenthèses ( en commençant par les multiplications ,…) les crochets
deviennent alors de simples parenthèses. |
|
||||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Exemple 1: A = [ 5
+ 6 |
|
|||||||||||||||
|
|
1°)
Vous effectuez le calcul dans les
parenthèses . ( Les crochets
deviennent des parenthèses ) A
= [ 5 + 6 2°)
Vous effectuez le calcul dans les
crochets . ( Les crochets qui sont
devenus des parenthèses ) A
= ( 269
) 3°)
A = 2152
+ 504
+ 6 4°) A = 2 662 |
|
|||||||||||||||
|
|
Exemple 2: Calculez comme
précédemment B
= [ 4 + 3 B
= [ 4 + 3 B
= [ 4 + 3 B
= [ 4 + 51
] B
= ( 55 )
B
= ( 330 ) + 9 +
( 800 ) B
= 1139 |
|
|||||||||||||||
|
|
Simplification de l’
écriture d’une suite de calculs par
suppression de parenthèses ou crochets. |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Grâce
à la règle de la priorité de la
multiplication sur l’addition, «
3 + ( 7 |
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
Exercice 3 : |
|
|||||||||||||||
|
|
Sans
effectuer de calculs , réécrivez en enlevant les parenthèses et les crochets
superflus. |
|
|||||||||||||||
|
|
C = ( 3 |
C = 3 |
|
||||||||||||||
|
D = (
4 + 8 |
D = ( 4 + 8 |
||||||||||||||||
|
E = 7 + ( 5 |
E = 7 + 5 |
||||||||||||||||
|
|
|
|
|||||||||||||||
|
|
·
Des parenthèses ,ou des crochets peuvent aussi s’enlever
grâce à l’associativité de la
multiplication ou de l’addition. |
|
|||||||||||||||
|
|
Exemples
: 7 + ( 5 + 3 ( 9 + 4 ) |
|
|||||||||||||||
|
|
Série d’exercices : Sans effectuer de calculs , réécrivez en
enlevant si possible les parenthèses
ou crochets. |
|
|||||||||||||||
|
|
F = 5
+ [ 3 |
F = 5 +
3 |
|
||||||||||||||
|
G =
[ ( 3 + 5 ) |
G = (
3 + 5
) |
||||||||||||||||
|
H =
[ 3 |
H = 3 |
||||||||||||||||
|
J =
( 5 + 7 ) |
J = ( 5
+ 7 ) |
||||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||
TRAVAUX AUTO
FORMATIFS (devoir formatif)
CONTROLE :
Compléter :