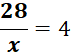Pré requis :

Algèbre : nomenclature , conventions


et les 4 opérations dans N
Addition	multiplication	soustraction	division

ENVIRONNEMENT du dossier:

Index warmaths	Objectif précédent	Objectif suivant	Suite : calcul algébrique : résoudre avec des nombres relatifs.

DOSSIER: Calcul algébrique de degré 1 (avec les nombres entiers naturels)

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

On dit aussi : Résoudre dans N :

4³iSOS COURS

COURS :

Cas général :

"" et "" sont des nombres entiers ;

"" l'inconnue ;

"*" (l'étoile) représente les signes opératoires :

"multiplié", "diviser" , "additionner", "soustraire" .

3 cas:
Lire :

	L'inconnue "" est associée à un nombre	L'inconnue "" est associée à un nombre	L'inconnue "" est le résultat final d'une opération effectuée entre deux nombres ,(cas du calcul numérique)

Approche théorique:

I cas : Soit deux nombres séparés par un signe opératoire:

Ces modèles sont rencontrés en Calcul Numérique :

"a" et "b" sont des nombres entiers

L ' équation est toujours de la forme "x"=…..

Il suffit de faire le calcul ! ! ! !: (avec ou sans calculatrice)

addition	multiplication	soustraction	Division ou fraction	Fraction ou division
			=	=
*SOS cours*	*SOS cours*	*SOS cours*	*SOS cours*	*SOS cours*

Exemple :	Exemple :	Exemple :	Exemple :	Exemple :
				=

Cas II :

Modèles :

calcul algébrique

" et "" sont des nombres entiers

Problème à résoudre: L ' équation doit toujours se ramener sous la forme ""=….. Pour trouver la valeur de ""

Problème à résoudre: L ' équation doit toujours se ramener sous la forme "

La transformation de l’égalité permettra de trouver la valeur de "x" qui vérifie que l’égalité est vraie .

Modèle 1	Modèle 2	Modèle 3	Modèle 5	Modèle 6

	ou ax = b
Idem : modèle 1	Idem : modèle2	Modèle 4

Il faut donc " Résoudre" : résoudre c'est rechercher la valeur numérique d ' une lettre (dite inconnue : x ) telle que cette valeur vérifie l' égalité "vraie".

Approche numérique ( applications) :

Modèles Calcul Numérique :	"a" et "b" sont des nombres entiers	L ' équation est toujours de la forme "x"=…..

conclusions
		4 - 7 est impossible, les N sont toujours "positifs"	Pas de solution puisque n 'est pas un entier	Idem que précédemment Il faut faire la division euclidienne ,le quotient doit être exacte.

Modèles calcul algébrique "a" et "b" sont des nombres entiers L ' équation doit toujours se ramener sous la forme "x"=….. Pour trouver la valeur de "x" De façon déductive, il faut se poser la question :quel peut être le nombre qui associé à « x » séparé par le signe opératoire …………….donne …………
Exemple 1	Exemple 2	Exemple 3	Exemple 4	Exemple 5

Ainsi :	Ainsi :	Ainsi :	Ainsi :	Ainsi :
Quel est le nombre qui "ajouté" à "7" donne 11? Réponse:4 Parce que 7+4 = 11	Quel est le nombre qui "multiplié" à "7" donne…28.? Réponse:4 Parce que 74 =28	Quel est le nombre qui "soustrait" à "7" donne…3.? Réponse:4 Parce que 7-4 = 3	Quel est le nombre qui "associé" à "x" donne……..? Réponse : 12 parce que 4fois 3 = 12 ; donc 12 divisé par 3 = 12	Quel est le nombre qui "associé" à "x" donne……..? Réponse : 7 parce que 7fois 4 = 28 ; donc 28 divisé par 7 = 4
Conclusion: x = 4	Conclusion: x = 4	Conclusion: x = 4	Conclusion : x = 12	Conclusion : x = 4

Comment doit s 'effectuer cette recherche de la valeur de « x »? : il y a deux méthodes : déductive ou par transformation menant à une opération du style x= .a. ..?…b

I ) Première méthode De façon déductive:

On affecte une valeur numérique à "x" ; on effectue le calcul ;on vérifie si l ' égalité est "vraie"

. On affecte une seconde valeur numérique à "x" ; on effectue le calcul ;on vérifie si l ' égalité est "vraie". Ainsi de suite , par approche successive .(méthode d'encadrement ) .

II ) Deuxième méthode en appliquant les théorèmes sur les égalités (niveau ++ )

procédure:

transformer les deux membres en somme algébrique .	SOS cours
Isoler le terme en "x" ; pour cela appliquer l ' un des 4 théorèmes	SOS cours

Exemple:

4 + x = 7

Première méthode: on attribue à "x" une valeur au hasard .(par encadrement )
1 essai : On donne à x la valeur "2" (c'est un exemple)
On remplace dans l 'égalité "x" par la valeur choisie 4 +2 ,et l ' on calcule =6
On compare les deux membres Le premier membre vaut "6" , le deuxième membre vaut "7" .
Première conclusion : les deux membres ne sont pas égaux ; alors on dit que "2" n 'est pas solution de l ' équation.
Il faut attribuer à "x" une autre valeur ; essayer de nouveau ; vérifier est conclure
La solution est 3;

Deuxième méthode: on applique les théorèmes des égalités: "transformations"
Cette méthode exige une grande quantité de connaissances qui ne seront acquises qu ' a la fin du calcul numérique.
Exemple : 4 + x = 7
(+4) + x = (+7)	Transformer l’expression en somme
(+4) + x + (-4) = (+7) + (-4)	Ajouter (-4) pour neutraliser le (+4)
x + ( + (4-4) ) = (+7) + (-4)	Faire la somme des nombres (+4) et (–4)
x + ( + (0) ) = (+7) + (-4)	Valeur absolue = 0
x + ( + 0 ) = (+7) + (-4)	Supprimer les parenthèses de la valeur absolue
x + 0 = (+7) + (-4)	Simplifier l’écriture (-0) par « 0 »
x = (+ ( 7-4))	Faire la somme des nombres du deuxième membre
x = (+ ( 3))	Résultat
En simplifiant x =3	Rendre compte
Faire la vérification : Est ce que : 4 +3 est égal à « 7 » Evidemment que « oui » donc la solution x =3 est vraie

Représentation graphique de la solution :

Pré requis

Point
Axe gradué

La représentation graphique de la « solution » est un point situé sur un axe gradué ( abscisse d’un point)

Travaux auto formatifs :

CONTROLE

1. Que signifie "résoudre"?

2. Que signifie "résoudre" dans N ?,

3. Donner deux méthodes permettant de trouver la valeur numérique qui vérifie l 'égalité "vraie".

EVALUATION

Résoudre dans N : ( justifier votre réponse)

7+ x = 11	7x =28	7 -x = 3	= 3	= 4
7+ x = 3	7x =19	7 -x = 5	= 9	= 2