Pré requis:
|
|
|
|
Objectif précédent : |
|
||
|
|
|
|
|
DOSSIER « calcul
numérique » : SOUSTRACTION
dans N
|
·
le sens de
l’opération, · La
soustraction est une opération, · Ordre de
grandeur d’une différence, · L’ ELEMENT NEUTRE DE LA SOUSTRACTION |
|||||||
|
COURS
|
|
||||||
|
|
|
|
|
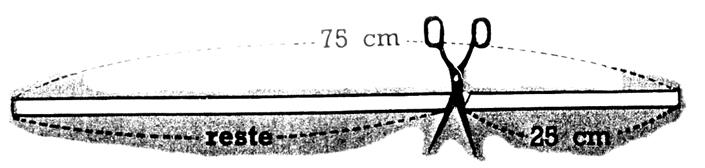
le sens de l’opération : Explication
n° 1 : mon ruban
mesure « 75 cm » : Je coupe ; je retranche ; je
retire « 25 cm d’un ruban de 75
cm » La soustraction
est « 75 - 25 » me dit : ce qui me reste
est « 50 cm » |
|||
|
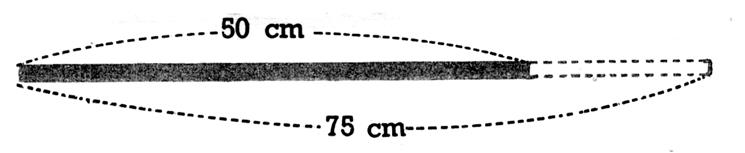
Explication n°2 :
Combien manque
- t- il à 50 cm pour que j’aie 75 cm ? Réponse : la soustraction
« 75 - 50 » me dit ce qui me manque : « 25» ; l’unité étant des
« cm » ; il me manque
« 25 cm ». |
|||
|
Explication n°3 :
« 75 cm » est plus
long que « 50 cm » , (c’est la règle
graduée qui permet de le mesurer) donc : « 50cm » est plus court que « 75
cm ». ; de combien ? on fera la soustraction
« 75 - 50 » ,
le résultat de ce calcul me donne la différence « 25 » ; |
|||
La soustraction est une opération :
la
soustraction de deux nombres est un
calcul qui consiste à Soustraire ( ou retrancher) :
c’est à dire d’ ôter des éléments à une somme d’éléments
existants .
Activité 1 : cherchons le nombre qu’il faut ajouter à 7 pour obtenir 10
10 = 7 + 3
Le nombre « 3 » est la
différence de 10 et 7 pris dans cet ordre .
On écrit alors 10 – 7 =
3 ; 10 et 7 sont les termes
de la différence .
L’opération correspondante s’appelle « soustraction »
Activité 2
Situation problème : on va chez le libraire acheter 2
livres pour un total de 41 € . le premier livre coûte 17 € . Nous
cherchons combien coûte le deuxième livre ;
41 = 17 + ? ; pour trouver le
résultat on fait la différence de 41 et 17
pris dans cet ordre : 41 –
17 = 24
donc
41 – 17 = 24 signifie
41 = 17 + 24
Activité 3 :
cherchons s’il est possible de calculer 11 – 14
Supposons
qu’il existe un entier naturel égal à 11 – 14 .
Dans ces conditions , 14 ajouté à ce nombre
serait égal à 11 , ce qui est
impossible car la somme de deux entiers
naturels est toujours supérieure ou égale
à chacun de ces nombres .
Donc il n’existe pas d’entier naturel égal à 11 – 14
On voit alors que si ce calcul
n’est pas possible , c’est parce que 11 < 14
Signe :
le signe indiquant que l’on doit faire une addition est « - » (attention à ne pas confondre du
nombre relatif négatif).
Résultat de la soustraction : le résultat de la soustraction est appelé
« différence ».
A
retenir : la différence de deux
entiers naturels pris dans un certain ordre est l’entier naturel ( s’il existe) qu’il faut ajouter au second pour obtenir le
premier .
Pour deux nombres entiers naturels , la soustraction n’est possible que si le premier
nombre est supérieur ou égal au second .
« a » - « b » = x signifie
« a » = « b » + x
Attention :
On ne
peut pas prendre plus de deux nombres pour faire une
soustraction.
ATTENTION : avec
les nombres entiers naturels l’ordre des nombres dans la soustraction est très importante : ON ne sait pas soustraire un grand nombre
à un petit nombre.
Exemple : l ‘opération 15 - 36 est impossible
donc l'opération ( a - b = c )
, n'est possible que si a > b:
si "b" est supérieur à
"a" l 'opération ne peut se faire ;
le résultat ne peut être un nombre
négatif; donc on dit que l ' opération est impossible .
l
‘opération 15 - 36 est impossible
Ordre de grandeur d’une différence:
Toutes
les fois que l’on doit faire une opération il faut estimer mentalement un ordre
de grandeur du résultat afin d’éviter de grossières erreurs lorsque l’on donnera le résultat.
Cette
démarche est importante lorsque l’on prend la calculatrice ,
l’erreur de manipulation étant fréquente il faut ou vérifier (refaire le
calcul) ou estimer le résultat que l’on devrait trouver.
Comme
pour une somme ,
on peut déterminer un ordre de grandeur d’une différence.
Activité : Cherchons un ordre de grandeur
de 58 476 – 21 435
Un ordre de grandeur de 58 476
est 60 000 et de
21 435 est 21 000 ; l’ordre de grandeur de la différence est
de 39 000
Calcul en primaire :
|
Série
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
9 |
|
8 |
|
5 |
|
7 |
|
6 |
|
|
8 |
|
4 |
|
5 |
|
10 |
|
|
|
- 6 |
|
- 5 |
|
- 4 |
|
- 4 |
|
- 8 |
|
|
- 6 |
|
- 4 |
|
- 3 |
|
- 6 |
|
|
= |
3 |
|
3 |
|
1 |
|
3 |
|
Impossible,
l’opération est mal posée.. |
|
2 |
|
0 |
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Série 2
|
|
1 9 |
|
1 8 |
|
1 5 |
|
1 7 |
|
6 |
|
|
1 8 |
|
1 4 |
|
1 5 |
|
20 |
|
|
|
- 6 |
|
- 5 |
|
- 4 |
|
- 4 |
|
- 1
8 |
|
|
- 6 |
|
- 4 |
|
- 3 |
|
- 6 |
|
|
= |
1 3 |
|
1 3 |
|
1 1 |
|
1 3 |
|
Impossible,
l’opération est mal posée.. |
|
1 2 |
|
1 0 |
|
1 2 |
|
1 4 |
|
|
Série 3
|
|
1 5 |
|
1 5 |
|
1 1 |
|
1 2 |
|
1 6 |
|
|
1 6 |
|
1 4 |
|
1 5 |
|
11 |
|
|
|
- 5 |
|
- 6 |
|
- 4 |
|
- 4 |
|
- 1
8 |
|
|
- 8 |
|
- 9 |
|
- 8 |
|
- 6 |
|
|
= |
1 0 |
|
9 |
|
7 |
|
8 |
|
Impossible,
l’opération est mal posée.. |
|
8 |
|
5 |
|
7 |
|
5 |
|
|
Opération de la soustraction
:
Pour effectuer une soustraction avec des
nombres entiers il est essentiel de bien aligner les chiffres ( ordre à ordre )
Procédure : (exemple :1536 - 227 = ? )
-
Tracer le tableau de numération des nombres entiers (peut se faire mentalement )
-
première ligne : Placer le
premier nombre dans le tableau (d’abord
le premier chiffre dans la colonne d’unités des unités « 6 » ) (exemple 1536 )
-
deuxième ligne : Placer le
deuxième nombre (227) sous le premier
nombre en respectant l ‘ordre de
numération « le 7 sous
le 6 » )
-
troisième ligne :
faire la soustraction
colonne par colonne en commençant par la colonne de droite (colonne des unités d ’ unités)
Remarque : lorsque , dans une
colonne donnée , le chiffre du deuxième
nombre est plus grand que le
chiffre du premier nombre ( exemple 6
- 7 ; impossible à calculer)
alors
retirer « 1 » au premier nombre , dans la
colonne suivante (de gauche) (ainsi 3 -1
= 2 )
( qui donne 1536 devient 152 0 +16 ; pour pouvoir faire 16 -7 = 8 ; donc 1536 -7 donne 1520 +8 =1528 )
placer
le premier chiffre du calcul dans la colonne correspondante ,
et rajouter « 1 » dans la colonne suivante (de gauche) et ainsi de suite à chaque fois que cela se
présente.
|
Classe
des milliards |
classe
des millions |
classe
des milles |
classe
des unités |
|||||||||
|
centaines |
dizaines |
unités |
centaines |
dizaines |
unités |
centaine |
dizaine |
unités |
centaines |
dizaines |
Unités : + 1 diz |
|
|
|
On retranche à 3 diz « 1 » dizaine que l’on rajoute dans la colonne des unités pour
faire 16 (10+6) en suite on calcule 16
-7 « = 9 »
;il reste donc un « 2 » dans la colonne des
dizaines. |
|
|
1 1 |
5 5 |
3 3 -1 = 2 diz. |
6 10+6= 16 (16-7=9) |
|||||
|
|
|
- |
|
2 |
2 |
7 |
||||||
|
|
|
|
|
|
|
|
= |
1 |
3 |
0 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Soit
en simplifiant :
|
|
|
|
|
|
|
|
|
|
1 |
5 |
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
- |
|
2 |
2 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
0 |
9 |
|
|
Vérification :
il suffit d’additionner le résultat plus le deuxième nombre pour retrouver la
valeur du premier nombre (
1309 + 227 = est bien égal à 1536)
L’ELEMENT NEUTRE DE LA SOUSTRACTION : EST « 0 » ; en effet 15
- 0 =15 ( a - 0 = a )
Pré
requis
|
Expression et somme algébrique |
|
|
Egalité théorème |
Exemples :
|
Résoudre |
Résultats
|
|
|
Colonne
1 |
|
|
|
1-… =
1 |
1 - x = 1 |
x =1 |
|
1 -
1 =….. |
1 - 1 = x |
x =0 |
|
8 - ….. =
5 |
8 - x = 5 |
x = 3 |
|
17 - ……=
10 |
17 - x = 10 |
x =7 |
|
43
-…. .= 32 |
43 - x = 32 |
x = 11 |
|
237
- ……..= 136 |
237 - x = 136 |
x =101 |
Corrigé des exemples :
|
Compléter
les opérations |
Résoudre |
Résultats |
|
Colonne 1 |
|
|
|
1-… = 1 |
1- x = 1 |
x =1 |
|
1 - 1 =….. |
1-1 = x |
x =0 |
|
8 - ….. = 5 |
8 - x = 5 |
x = 3 |
|
17 - ……= 10 |
17 - x = 10 |
x =7 |
|
43 -…. .= 32 |
43 - x = 32 |
x = 11 |
|
237 - ……..= 136 |
237 - x = 136 |
x =101 |
TRAVAUX AUTO FORMATIFS.
|
|
1 ) Tracer le tableau de numération des
nombres entiers :
2 )Comment appelle - t
on le résultat de la soustraction?
3 ) donner la procédure concernant la
disposition des nombres et l’effectuation de la soustraction.
4 ) quel est le signe de la soustraction.
5. ) quel signe trouve-t-on
entre (10-3 ) .... ( 7 )
6. ) On dit que la soustraction , dans
des nombres de l'ensemble des entiers naturels, et l'ensemble des nombres décimaux positifs ;
l'opération ( a - b = c ) , n'est possible
que si a > b:
Expliquez en vous aidant
de deux exemples ( un
possible et un non possible).
7 ) .Que signifie le symbole " " ?
8 ).Donner la ou les façons de vérifier
l'exactitude du résultat.
|
|
Effectuer les opérations suivantes: Effectuer les soustractions suivantes
, après les avoir posées ( En
l'état de nos connaissances certaines
opérations ne sont pas faisables ,dite pourquoi
)
|
exercices |
résultat |
Corrigé ou commentaire |
|
4- 3 = |
|
|
|
9 - 7 = |
|
|
|
17 - 6 = |
|
|
|
28 - 10 = |
|
|
|
57 - 69 = |
|
|
|
157 - 42 = |
|
|
|
185- 38 = |
|
|
|
246 - 123 = |
|
|
|
568 - 479 = |
|
|
|
1 365 - 432 = |
|
|
|
2684 - 2 857 = |
|
|
|
12 589 - 10698 = |
|
|
INTERDISCIPLINARITE
|
1.
J' avais 5
pommes .J'en donne 3 à mon frère. Combien m'en reste - t -
il ? |
|
2.
J'avais 4 francs. J'en ai dépensé 2 .Combien m'en
reste - t - il
? |
|
3.
Dans une cabane il y avait 5 lapins
. J'en retire 2 Combien en reste - t -i l ? |
|
4.
Sur le buffet , il y
avait 5 assiettes et 3 bols. On casse
1 bol et 2 assiettes
. Combien reste - t - il
de bols et d'assiettes ? |
|
5.
A la cave il y avait 4 bouteilles de vin et 4
bouteilles de cidre . On a but 1 bouteille de vin et 2 bouteilles de cidre . Que reste - t - il à la
cave ? |
6- Michel reçoit 100 € pour son anniversaire . Il décide d’ acheter
une montre . Après l’avoir payée , il fait le
compte de ses économies . Il
s’aperçoit alors qu’il possède 30 €
de moins qu’avant son anniversaire .
Quel est le prix de la
montre ?
7 - Le capitaine d’un bateau a 5 ans de plus que son second Le bateau a été lancé il y a 11 ans . Sachant que le second
est entré en service 4 ans après le lancement du bateau à l’ âge de 28 ans .
Quel est l’âge du capitaine ?
8 - Un récipient de 29 l
peut-être rempli par le contenu de 3 seaux .
Le premier et le deuxième seau
contiennent ensemble 22 l . Le deuxième et
le troisième seau contiennent ensemble
20 l .
Quelle est la contenance de chacun des seaux ?