Pré requis:
|
|
|
|
ť |
|
|
ť |
|
|
Lecture : Notions de grandeur ,
de « numération et de nombre |
ť |
|
ť |
|
|
ť |
|
|
|
|
|
|
CLASSE
6čme ( avant 2000) |
|
Objectif
précédent: Cours
précédent ( 6čme ) sur :l es entiers |
Dossier N°
|
Suite : la soustraction de nombres entiers
naturels. |
1°)Tableau 14 2°)
liste des activités dans N 3°)
les N en primaires.( travaux et rappels de cours) Info
+++ : Les entiers naturels. |
DOSSIER : LES ENTIERS
NATURELS (symbole : N ) : La soustraction
|
|
|
|
|||||
|
|
2°)
SOUTRACTION des entiers naturels |
|
|||||
|
|
a) découverte ; b)égalités ayant le
męme signification ; c) ordre de grandeur
d’une différence, d) calcul mental :
ajouter ,retrancher ; |
|
|||||
|
|
e)
Problčmes avec des entiers naturels |
|
|||||
|
|
|||||||
|
|
|||||||
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Aller vers
: Numération romaine |
|
|
|
|
|
|
COURS
|
|
|
|
|
|
||||||||||
|
|
SOUSTRACTION
des entiers naturels |
|
||||||||||
|
|
|
|
||||||||||
|
|
Cherchons le nombre qu’il faut ajouter ŕ
« 7 » pour obtenir « 10 »
soit : 10 = 7 + ….
( 3) Le nombre « 3 » est appelé la différence de « 10 » et
« 7 » pris dans l’ordre.. On écrit alors « 10 – 7 = ….. » ;
« 10 » et « 7 » sont
appelés les termes de la
différence. L’opération correspondante s’appelle la « soustraction » |
|
||||||||||
|
|
·
Exemple
de situation problčme : Vous allez chez le
libraire et vous acheté 2 livres pour un total de 42 € . Le premier livre coűte
17 € . Cherchons combien coűte le deuxičme livre. 42 = 17 + ……. Pour trouver le résultat on fait la différence de
« 42 » et « 17 » pris dans cet ordre. 42 - 17
= ………. |
|
||||||||||
|
|
|
42 –
17 = …25.. signifie que : 42 = 17 + 25 |
|
|
||||||||
|
|
|
|
||||||||||
|
|
·
Cherchons si il est possible de
calculer 13 – 15 |
|
||||||||||
|
|
Supposons qu’il existe un entier naturel ( ?
) égal ŕ la soustraction « 13 –
15 » |
|
||||||||||
|
|
Dans ces conditions , « 15 »
ajouté ŕ ce nombre ( ?) serait égal ŕ « 13 » Ce qui est
impossible car la somme de deux entiers naturels est toujours
supérieure ou égale ŕ chacun de ces nombres. Donc il n’existe pas d’entier naturel égal ŕ
« 13 – 15 ». |
|
||||||||||
|
|
On voit alors que si ce calcul n’est pas
possible, c’est parce que « 13
< 15 » ( 13 est inférieur ŕ
15) |
|
||||||||||
|
|
|
|
||||||||||
|
|
A
retenir : |
|
||||||||||
|
|
La différence de deux entiers naturels pris dans un ordre certain
(dans un certain ordre) est l’entier naturel ( si il existe) qu’il faut
ajouter au second pour obtenir le premier.
Pour deux nombres entiers naturels , la soustraction n’est possible que
si le premier nombre est supérieur ou égal au second. |
|
||||||||||
|
|
|
|
||||||||||
|
|
|
« a - b = x » signifie
que « a = b + x » |
|
|
||||||||
|
|
|
|
||||||||||
|
|
·
Calcule si cela est
possible : 7 – 4
= …………………… et 4 – 7 = ……………….. |
|
||||||||||
|
|
Peut- on
7 – 4 = ? =
4 – 7 |
|
||||||||||
|
|
On doit en déduire que la soustraction n’est pas
commutative. |
|
||||||||||
|
|
|
(
35 – 17 ) – 8 =………………………….. =……………………………. |
35 -
( 17 – 8 ) =………………………………… =……………………………….. |
|
|
|||||||
|
|
Trouvez vous le męme résultat ?
……………………………………….. Donc ( 35 – 17 )- 8 La place des parenthčses importe
–t-elle ?..................................................................................... On en déduit que la soustraction
………………………………………………………………………. |
|
||||||||||
|
|
|
|
||||||||||
|
|
Exercice : |
|
||||||||||
|
|
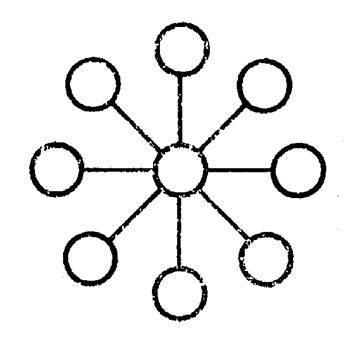
Disposez les nombres 1 ; 2 ; 3 ; 4 ;
5 ; 6 ; 7 ; 8 ; 9 ; dans les ronds de l’étoile ci
contre de telle sorte que la somme sur
« chaque ligne » soit égale ŕ « 15 » |
|
|
|||||||||
|
|
b)
Egalité ayant la męme signification. |
|
||||||||||
|
|
Dans chacune des lignes ci-dessous, les égalités
ont la męme signification. Complétez ces égalités en commençant par celle
qui vous paraît la plus facile. |
|
||||||||||
|
|
|
|
||||||||||
|
|
13 -
8 =………… |
« signifie » |
13
= …….+ ……… |
« signifie » |
13 -
…… = 8 |
|
||||||
|
25 -
4 =………… |
« signifie » |
……=……………………. |
« signifie » |
……………………………. |
||||||||
|
54 -
… =…26… |
« signifie » |
………..= …….+ ……… |
« signifie » |
………….-……….=………. |
||||||||
|
………….-
14 = 23 |
« signifie » |
………..= …….+ ……… |
« signifie » |
……….-……….=…14
. |
||||||||
|
25
– 0 = …………. |
« signifie » |
………..= …….+ ……… |
« signifie » |
…………………………….. |
||||||||
|
13
– 17 = ……………. |
« signifie » |
13 = 17 + ………. |
………………………………………………………………….. |
|||||||||
|
27
– 27 = ……………… |
« signifie » |
………..=
…….+ ……… |
« signifie » |
……………………………….. |
||||||||
|
28
- …………..= 32 |
« signifie » |
28
= ………+ 32 |
…………………………………………………………… |
|||||||||
|
|
|
|
||||||||||
|
|
c)
Ordre de grandeur d’une différence. |
|
||||||||||
|
|
Comme pour une somme, on peut déterminer un ordre
de grandeur d’une différence. |
|
||||||||||
|
|
Exemple :
Cherchons un ordre de grandeur de
« 58 399 – 21 356 » |
|
||||||||||
|
|
Cherchons l’ordre de grandeur de chaque
nombre : « l’ordre de grandeur de 58 399 est
59 000 , ( ou il est possible :
60 000 ) »
; « l’ordre de grandeur de
21 356 est
21 000 (ou
il est possible : 20 000 ) » |
|
||||||||||
|
|
Un ordre de grandeur de « 58 399 –
21 356 » est « 59 000
– 21 000 soit 38 000» ou il est possible « 60 000 – 20 000 soit 40 000 » le
résultat est donc proche de 38 000 pour un cas ou 40 000 pour l’autre
cas . |
|
||||||||||
|
|
|
|
||||||||||
|
|
||||||||||||
|
|
1°) Ajouter « 9 » ;
« 19 » ; « 29 » ;……etc. |
|
||||||||||
|
|
·
on sait que « 9 = 10 -1 » , ainsi :
ajouter « 9 » revient ŕ ajouter « 10 » puis retrancher « 1 » |
|
||||||||||
|
|
|
|
||||||||||
|
|
Exemple : 46 + 9
= (46 + 10) - 1
= 55 |
|
||||||||||
|
|
|
|
||||||||||
|
|
Le
chiffre des dizaines a augmenté de « 1 » et le chiffre des unités a
diminué de »1 ». |
|
||||||||||
|
|
Compléter : |
|
||||||||||
|
|
57 +
9 = |
95 + 9 = |
143 + 9 = |
|
||||||||
|
|
|
|
||||||||||
|
|
·
19 = 20 -1 ; 65 + 19 = ( 65 + 20 ) – 1 = 85 -1
= 84 |
|
||||||||||
|
|
Compléter : |
|
||||||||||
|
|
48 + 19 = |
27 + 69 = |
39 + 123 = |
|
||||||||
|
54 + 159 = |
54 + 109 =
|
637 + 999 = |
||||||||||
|
|
|
|
||||||||||
|
|
Remarque ; de la męme façon 25 + 8
= ( 25 + 10 ) – 2 = 35 – 2
= 33 |
|
||||||||||
|
|
Et 34 + 27
= ( 34 + 30
) – 3 = 64 – 3 =
61 |
|
||||||||||
|
|
Compléter : |
|
||||||||||
|
|
44 + 38 = ………………….. |
56 + 98 = ………………. |
25 + 107 = ……………… |
|
||||||||
|
|
|
|
||||||||||
|
|
|
|
||||||||||
|
|
2°) Retrancher
« 9 » ; « 19 » ;
« 29 » ;……etc. |
|
||||||||||
|
|
·
9
= 10 – 1 ; retrancher « 9 » cela
revient ŕ retrancher « 10 »
et ajouter « 1 » |
|
||||||||||
|
|
|
|
||||||||||
|
|
Exemple : 57
- 9 = ( 57 – 10) + 1 = 47
+1 = 48. |
|
||||||||||
|
|
Le
chiffre des dizaines a diminué de « 1 » et le chiffre des unités a
augmenté de « 1 ». |
|
||||||||||
|
|
Compléter : |
|
||||||||||
|
|
43 - 9 = |
58 – 9 = |
352 – 9 = |
|
||||||||
|
|
|
|
||||||||||
|
|
·
39 = 40 – 1 |
|
||||||||||
|
|
62
– 39 = ( 62 – 40) +1 = 22 + 1 = 23 Compléter : |
|
||||||||||
|
|
73 – 19 = |
54 – 49 = |
143 – 59 = |
|
|
|||||||
|
|
378 – 299 = |
653 – 109 = |
2 728 – 999 = |
|
|
|||||||
|
|
|
|
||||||||||
|
|
Remarque : de la męme façon : 72 –
28 =
( 72 – 30) + 2 = 42 + 2 = 44 |
|
||||||||||
|
|
|
|
||||||||||
|
|
Compléter : |
|
||||||||||
|
|
100- 37 = |
123 – 98 = |
200 – 37 = |
|
||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
.
|
|
Situations problčmes |
|
|
|
|
N°1 : Une cuve ŕ vin contient
2500 litres. ( l ) On soutire une premičre fois 557 l Une deuxičme fois on soutire 824 l On en soutire encore une troisičme fois . Combien a-t-on soutiré de vin la troisičme fois ? |
|
|
|
|
|
|
|
|
|
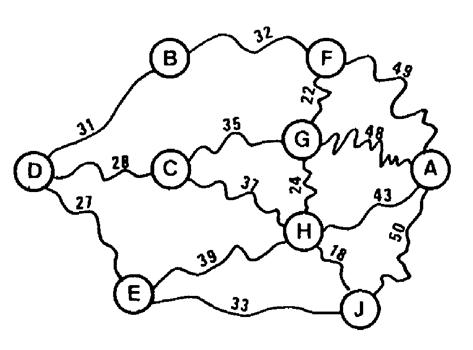
Voici , ci contre un extrait de carte . Les lettres dans les cercles
représentent les villes. Les nombres sur les lignes indiquent la distance en km entre deux
villes. Questions : 1. Trouvez le plus
court chemin pour aller de « D » ŕ « A ». Pour cela il faut calculer la longueur des différents parcours
possibles. Exemple : Longueur du chemin « DBFA « = 31 + 32 + 49 = 112
|
|
|
|
|
Problčme n°3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Multiplication : |
|
|
|
|
Pb.1 : On veut planter
des arbres fruitiers dans un jardin. Pour cela on achčte 5 pommiers ŕ 62 € l’un ; 3 poiriers ŕ 73 € l’un , 2 pruniers ŕ 84 € l’un et 4
cerisiers ŕ 89 € . Quelle est la dépense ? |
|
|
|
|
|
|
|
|
|
Pb2 : Caroline est née le 14 décembre
1975 ŕ 9 h. le 14 décembre 1986 ŕ 9 h , elle calcule le nombre de jours ,
puis le nombre d’heures qu’elle ŕ vécu. Vous allez l’aider.* 1°) Calculez d’abord mentalement un ordre de grandeur du nombre d’heures
. Vous trouvez ?........................................ 2°) Calculez le nombre de jours exact ,puis le nombre d’heures (
attention aux années bissextiles : 1972 ; 1976 ; 1980 ;1984 ;1988
) |
|
|
|
|
|
|
|
|
|
Pb 3 : On veut numéroter les pages d’un cahier ayant 136 pages. 1°) Combien de chiffres devrez vous écrire en tout ? 2°) Combien de fois écrirez vous le chiffre « 1 » ? |
|
|
|
|
|
|
|
|
|
Pb4 : 5 enseignants se rencontre ŕ 7 h 50 mn en salle de
professeurs, ils se saluent et chacun serre la mian de ses autres collčgues. Combien y a – t-il en tout de poignées de mains. ? |
|
|
|
|
|
|
|
|
|
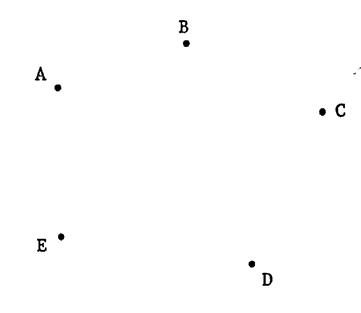
Voici cinq points « A » ;
« B » ; »C », »D » et « E ». 1°) On trace toutes droites
possibles contenant deux de ces points. Combien en tracez vous ? 2°) Retrouvez ce nombre par le calcul. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|