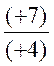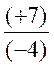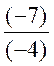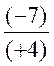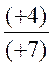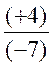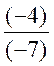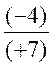Pré requis:
|
|
|
|
|
|
|
|
DOSSIER: Calcul algébrique « basiques » sur
comment :
Résoudre des équuations
algébriques avec des nombres Décimaux
relatifs (dit :
nombres algébriques)
Environnement du dossier:
|
Dossier : CN 60 |
On donne une équation est donnée :
On demande de résoudre l’équation du type : a *
x = b
L’astérisque est un signe opératoire qui peut être celui de : ( la multiplication ,
addition , soustraction , division…)
où a et b sont des nombres
décimaux relatifs et l' étoile peut
représenter l’un des 4 signes des opérations de base (
addition ;soustraction ; multiplication; division )
Approches
théoriques:
1° ) "a" et "b" sont des nombres
décimaux relatifs
2° )
L ' équation est toujours de la forme "x"=…..
|
Les modèles en Calcul Numérique
: (en calcul
numérique on pose x =…. ) Présentation de
l’égalité :Par « habitude » ; on met à gauche du signe égal les nombres séparés
par un signe opératoire , de l’autre côté du signe égal il y a le
« x » ; qui sera le
résultat du calcul |
||||
|
Modèle type n°1 |
Modèle type n°2 |
Modèle type n°3 |
Modèle type n°4 |
Modèle type n°5 |
|
a + b = x |
a b = x |
a -b = x |
|
|
|
Modèles
des équations du premier degré types à résoudre en « algèbre » "a" et "b" sont des nombres
décimaux relatifs, et la lettre « x » est un nombre à découvrir … On pose :« x »
est une lettre qui correspondra à une
valeur numérique , il faut transformer l’égalité pour que celle-ci soit une équation
a forme "x"=….. ; pour
transformer cette égalité il
faut respecter les règles de calcul vues en « calcul
numérique » ; « appelées : théorèmes» Pour
trouver la valeur de "x" |
||||
|
a + x = b |
a |
a -x = b |
|
|
Aucun calcul n’est possible ; ce que l’on peut
chercher c’est trouver un nombre
remplaçant « x » et vérifiant que l’égalité est une égalité
« vraie » ; on cherche à
résoudre un problème :
Exemples :
1°) Quelle
est la valeur que l’on pourrait donner à « x » pour que «3 + x =
5 » ?
Réponse : il n’y a pas d’autres solutions
que de connaître la table des additions :
On sait que
3 + 2 = 5 ; donc 5-3 = 2 ; ainsi pour que
3 + x donne = 5 , la valeur de « x » sera
égale à 2 .
2°) Quelle
est la valeur que l’on pourrait donner à « x » pour que «8 - x =
5 » ?
Réponse : il n’y a pas d’autres solutions
que de connaître la table des soustractions :
On sait que
8 – 3 = 5 ; donc 5 + 3 = 8 ; ainsi pour que
8 - x donne
= 5 , la valeur de
« x » sera égale à 3 .
3°)Quelle est la valeur
que l’on pourrait donner à « x » pour que «3 fois x = 15 » ?
Réponse : il n’y a pas d’autres solutions
que de connaître la table des divisions :
On sait
que 3 fois 5 = 15 ; donc 5-3 =
2 ; ainsi pour que 3 + x
donne = 5 , la valeur de « x » sera
égale à 2 .
4°)Quelle est la valeur
que l’on pourrait donner à « x » pour que «3 + x = 5 »
?
Réponse : il n’y a pas
d’autres solutions que de connaître la table des additions :
On sait que 3 + 2 = 5 ; donc
5-3 = 2 ; ainsi pour que 3 + x
donne = 5 , la valeur de « x » sera
égale à 2 .
« Résoudre » : résoudre c'est rechercher
la valeur numérique d
' une lettre (dite inconnue : x )
tel que cette valeur vérifie l' égalité
"vraie".
Dans D +ou -
|
4 cas pour l '
addition |
|
Solution : |
|
(+7)+(+ 4) = x |
|
X = (+11) |
|
(+7)+(- 4) = x |
|
X = (+3) |
|
(-7)+(- 4) = x |
|
X = (-11) |
|
(-7)+(+ 4) = x |
|
X=(-3) |
|
4 cas pour la multiplication |
|
|
|
(+7) |
|
X=(+28) |
|
(+7) |
|
X=(-28) |
|
(-7) |
|
X = (+28) |
|
(-7) |
|
X=(-28) |
|
4 cas pour la soustraction |
transformation |
|
|
(+7)-(+ 4) = x |
(+7)+ (- 4) =
x |
X =(+3) |
|
(+7)-(- 4) = x |
(+7)+(+ 4) = x |
X =(+11) |
|
(-7)-(- 4) = x |
(-7)+(+ 4) = x |
X = (-3) |
|
(-7)-(+ 4) = x |
(-7)+(- 4) = x |
X = (-11) |
|
4 cas pour la division |
|
|
|
|
|
X= (+1,75) |
|
|
|
X= (-1,75) |
|
|
|
X= (+1,75) |
|
|
|
X= (-1,75) |
|
idem |
« x » = n’a pas d’existence décimale. ( la division ne tombe pas juste ;si l’on veut un nombre décimal il
faudra donner une valeur arrondie ) ; on se contente de donner le signe
du résultat. |
|
|
|
|
+ |
|
|
|
- |
|
|
|
+ |
|
|
|
- |
APPROCHE ALGEBRIQUE :
L ' équation doit toujours
se ramener sous la forme "x"=…..
Comment doit s 'effectuer
cette recherche ? :
I ) Première méthode De
façon déductive:
On affecte une valeur numérique à "x" ;
on effectue le calcul ;on vérifie si l ' égalité est
"vraie"
.
II ) Deuxième méthode en appliquant les théorèmes sur les égalités
(niveau ++ )
procédure:
transformer les deux membres en somme algébrique . SOS cours
Isoler le terme
en "x" ; pour cela appliquer l ' un
des 4 théorèmes
exemple
4 + x = 7
|
Première
méthode: on attribue
à "x" une valeur au hasard . |
Deuxième
méthode: on applique les théorèmes des égalités: |
|
1 essai : On donne à x la
valeur "2" (c'est un exemple) |
Cette méthode exige une grande quantité de connaissances qui ne seront
acquises qu ' a la fin du calcul numérique. |
|
On remplace dans l 'égalité " |
|
|
On compare les deux membres Le premier membre vaut "6" ,
le deuxième membre vaut "7" . |
|
|
Première conclusion : les deux membres ne sont pas égaux ; alors on
dit que "2" n 'est pas solution de l ' équation. |
|
|
Il faut attribuer à " |
|
|
La solution est 3; |
|
Dans D +ou –
|
Il y 4 cas pour l ' addition |
|
|
|
1.
|
|
|
|
2.
|
|
|
|
3.
|
|
|
|
4.
|
|
|
|
Il y a 4 cas pour la multiplication |
|
Ecritures
équivalents : |
|
5.
|
|
|
|
6.
|
|
|
|
7.
|
|
|
|
8.
|
|
|
|
Il y a 4 cas pour la soustraction |
|
|
|
1.
|
(+7)-(+ 4) = x |
|
|
2.
|
(+7)-(- 4) = x |
|
|
3.
|
(-7)-(- 4) = x |
|
|
4.
|
(-7)-(+ 4) = x |
|
|
Il y a 4 cas pour la division |
|
|
|
|
5.
|
|
|
|
|
6.
|
|
|
|
|
7.
|
|
|
|
|
8.
|
|
|
|
|
idem |
|
|
|
9.
|
|
|
|
10. |
|
|
|
11. |
|
|
|
12. |
|
|
|
Modèles calculs algébriques |
" |
|
Pour
trouver la valeur de "x" |
|
|
(+7)+ (+ 4) = x (+7)+ (-
4) = x (-7) + (- 4) = x (-7) + (+ 4) = x |
(+7) (+7) -7) (-7) |
|
|
|
L ' équation doit toujours
se ramener sous la forme "x"=…..
TRAVAUX AUTO FORMATIFS.
CONTROLE
1°) Que signifie "résoudre" ,
2°) Donner
deux méthodes permettant de trouver la valeur numérique qui vérifie l 'égalité "vraie".
EVALUATION : refaire les exemples….