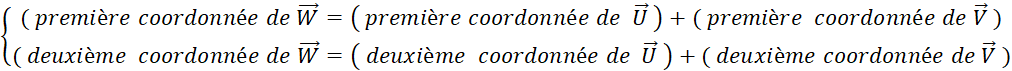Vers : Programme de troisième Collège.
Fiche sur la COMPOSITION DE TRANSFORMATION.
	Fiche 1 : Image de figures usuelles par des transformations.
	Fiche 2 : Rotation.
	Fiche 3 : Composition de deux symétries centrales.
	Fiche 4 : Composition de deux symétries orthogonales d’axes parallèles.
	Fiche 5 : Composition de deux symétries orthogonales d’axes perpendiculaires.
	Fiche 6 : Composition de translation.( et somme de vecteurs)
Pré requis:		Aller au corrigé .
Les transformations géométriques (liste)

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent 1°) Déplacement . 2°) voir le cours résumé sur les transformations géométriques.

Objectif suivant 1°) translation 2°) rotation 3°) rotation et translation conjuguées 4°)les propriétés des transformations géométriques

· liste « géométrie plane » Les vecteurs.

		Rappels :
		LES TRANSFORMATIONS GEOMETRIQUES ( COMPOSITION ) :
Liste des transformations principales :
1°) Les divers « déplacements » :
	· Translation
	· Rotation
2°) les oppositions ou symétries, qui, en géométrie plane , sont des cas particuliers de déplacements.
	· Symétrie centrale
	· Symétrie orthogonale
3°) les divers modes de projections
	· Projection par rapport à une direction quelconque.
	· Projection orthogonale
4 °) l’homothétie
5°) la similitude

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Fiches sur la COMPOSITION DE TRANSFORMATIONS . Composition de translations et somme vectorielle. ( de deux vecteurs) « Le vecteur – somme. »
Fiche 6 : Composition de translation.
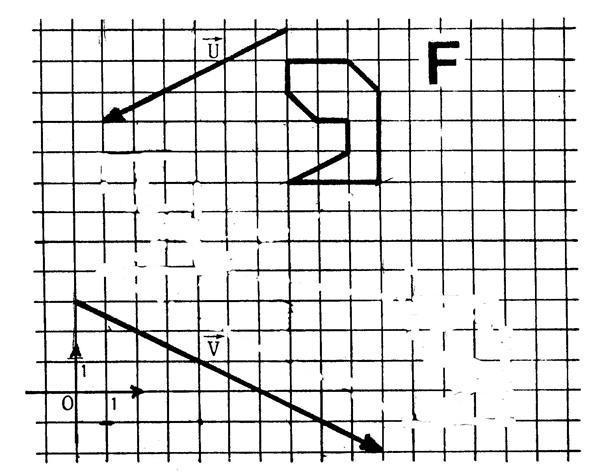
Ci-dessous : Dans le plan muni d’un repère, on donne deux vecteurs et et une figure « F ». -
On vous demande de dessiner l’image « F’ » de la figure « F » dans la translation de vecteur puis l’image « F’’ » de la figure « F’ » dans la translation de vecteur .
Observation : Il semble que « F’’ » soit l’image de « F’ » par une ……………………... Dessinez près de « F » et « F’’ » un représentant du vecteur de cette translation.
Appelons «  » ce vecteur .
Lisez ( sur le dessin) ses coordonnées : vous trouvez : «   ( ) » ; ( vous comptez le nombre de cases pour «  » , sens gauche à droite )
Lisez les coordonnées du vecteur , vous trouvez  »
Lisez les coordonnées du vecteur , vous trouvez  »
Vous remarquez que : ( pour «  ») «  » ( pour «  ») «  »	Rappel calcul : addition de deux nombres relatifs de signe contraire.
Nous allons démontrer ce que vous venez de constater :
Ø Choisissons un point « M » quelconque de « F » . Appelons ( ) ses coordonnées : «  M ( ) » Appelons « M ’ » l’image de « M » dans la translation de vecteur «  » Grâce au théorème vu dans la fich vu …N°5, translation de vecteur ;…. .. ; on peut écrire «  M ’  ; ) »
Appelons « M’’ » l’ image de « M’ » dans la translation de vecteur « »  Grâce au même théorème on peut écrire : «  M’’ ; ) »
C'est-à-dire : «  M’’  »
Calculons les coordonnées de «  » .  grâce au théorème vu …Fiche n°5, translation de vecteur ;…. .. on peut écrire : « «   » c'est-à-dire  «  » Quel que soit le point « M » de « F » et son image « M ’’ » de « F ‘’ » , « » a toujours pour coordonnées
Ces coordonnées sont celles de   . On peut donc dire : quel que soit « M » , «
On passe donc de « F » à « F’’ » par ………………….. de vecteur .
Enoncez , verbalement , la relation qui existe entre les coordonnées de «  » de « » et de « » .
Ø Il en est toujours ainsi quelque soient les vecteurs «  » et « » . On dira alors :
Théorème : La composée d’une translation de vecteur «  » et d’une translation de vecteur « »  est une translation dont le vecteur « »  est tel que :
Définition : Le vecteur « » est appelé vecteur –somme de «  » et de « »  et on peut écrire : « »