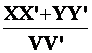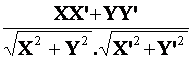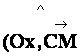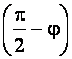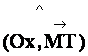Pré requis:
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : 1°) « direction » 2°) Projection
d’un point sur une droite … 3°) Les
relations trigonométrique |
|
Info générales : |
|
|
Objectif suivant : Voir la projection dans l’espace ( à venir) … |
Module : LES VECTEURS
DOSSIER Le théorème des projections , dans un plan .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité : |
|
COURS
|
|
Le
théorème des projections comporte deux parties essentielles : a)
La mesure algébrique de la projection
sur un axe orienté de la somme géométrique d’un système de
vecteurs est égale à la somme des mesures algébriques des projections des
vecteurs sur le même axe…Cette propriété est vraie en projection parallèle
quelconque. |
|
|||||
|
|
b) La mesure algébrique de la
projection orthogonale d’un
vecteur sur un axe orienté est égale
au produit de la mesure algébrique du vecteur par le cosinus de
l’angle des directions positives de l’axe et du support du vecteur . |
|
|||||
|
|
Remarque :Dans ce
cours la trigonométrie portera sur les angles saillants , donc compris entre
zéro et 180 degrés. Ce qui bien sur limite singulièrement l’étude du champ
d’application de ce théorème très général. |
|
|||||
|
|
|
|
|||||
|
|
Applications : des
exemples de problèmes… |
|
|||||
|
|
Problème
1 : |
|
|||||
|
|
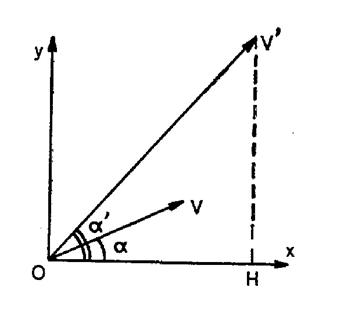
Soit un système d’axes
orthonormés « O x ; 0 y » . Un premier vecteur
On demande de calculer
en fonction de « X »
« Y » » X ’ » « Y ’ » le cosinus de l’angle |
|
|
||||
|
|
Solution : |
|
|||||
|
|
Puisque nous avons
l’angle ( O x , La seconde partie du
théorème des projections nous donne : |
|
|||||
|
|
|
X = V cos. Et Y = V sin
|
X ‘ = V
‘ cos. Et Y ‘ = V
sin |
|
|
||
|
|
|
|
|||||
|
|
D’ où : V 2 = X 2 + Y 2 et V ‘ 2 = X ‘ 2 + Y ‘ 2 |
|
|||||
|
|
|
|
|||||
|
|
Projetons
orthogonalement « V ‘ » en
« H » sur « Ox » |
|
|||||
|
|
|
|
|
|
|
||
|
Tracer sur le dessin les projections !!! |
|||||||
|
|
Mais le contour
polygonal « OH V ’ » permet d’écrire :
|
|
|||||
|
|
Projetez les éléments
de cette relation vectorielle sur le support de Ainsi , d’après la première partie du
théorème des projections nous pouvons écrire :
|
|
|||||
|
|
A savoir : ·
le cosinus de l’angle formé par le couple ( ·
le cosinus de l’angle formé par le couple : ( Ox , ·
le cosinus de l’angle formé par le
couple : ( |
|
|||||
|
|
D ’après la deuxième
partie du théorème des projections nous pouvons écrire : V ‘ cos . ( nota : « O y » est le sens positif qui porte le
vecteur donc V ‘ cos . Et comme d’après le
début de la solution : |
|
|||||
|
|
|
cos . |
sin. |
|
|
||
|
|
On a finalement :
cos . Ou : cos
. |
|
|||||
|
|
|
|
|||||
|
|
Problème 2 : |
|
|||||
|
|
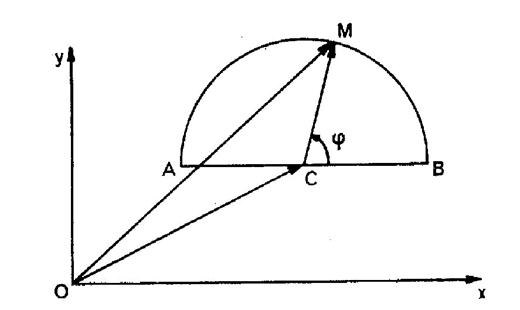
On considère un demi
cercle de centre C Calculer en fonction
de |
|
|
||||
|
|
Envisageons le contour
polygonal « OCM » et écrivons : I ) Projetons sur l’axe des « x » :
|
|
|||||
|
|
et d’après la seconde
partie du théorème des projections et compte tenu du fait que : ·
·
nous aurons : ·
« x = 8 + CM cos ( ·
« x = 8 + 5 cos ( |
|
|||||
|
|
II ) Projetons
sur l’axe des « Oy » : |
|
|||||
|
|
Compte tenu du fait
que : ·
·
Et cos ( Nous aurons : y = 5 + 5 sin . Les coordonnées du
pont « M » sont donc : |
|
|||||
|
|
M |
x = 8 + 5 cos y = 5 + 5 sin . |
|
|
|||
|
|
|
|
|||||
|
|
Problème 3 : |
|
|||||
|
|
On considère deux axes
rectangulaires orthonormé « O x »
et « O y » et un point « C » sur « O y »,
d’ordonnée « R ». Soit le demi-cercle, situé dans l’angle « x On défini un point « M »
de ce demi-cercle par l’angle formé
par les deux vecteurs : Calculer en fonction de « R » et l’angle |
|
|||||
|
|
Ce qui donne
comme début de solution : *Indications :
Et projeter sur les axes : |
|
|||||
|
|
|
« x = R sin « y = R – R cos . |
|
|
|||
|
|
|
|
|||||
|
|
Problème 4 : |
|
|||||
|
|
On considère deux axes
orthonormés « O x ; O y »et
le quart de cercle de centre « O », de rayon « a » ,
situé dans l’angle « x O y ». Soit « M » un
point de ce quart de cercle de centre ,défini par l’angle formé par « Ox » et le vecteur On oriente la tangente en « M » dans le sens |
|
|||||
|
|
et on porte sur cette tangente le vecteur
calculer en fonction
de « a » et de « |
|
|||||
|
|
|
|
|||||
|
|
Ce qui donne
comme début de solution : *Indications : Ecrire : et projeter sur les axes. |
|
|||||
|
|
|
« x = a (
cos. « y = a ( sin. |
|
|
|||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
TRAVAUX AUTO FORMATIFS. |
|
|||||
|
|
|
|
|||||
|
|
CONTROLE |
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
EVALUATION. |
|
|||||
|
|
Refaire les problèmes…du cours …… ;;;; |
|
|||||
|
|
|
|
|||||