Pré requis:

Le repérage.
Les Statistiques info
Lieu géométrique : INFO

ENVIRONNEMENT du dossier:

Index

Objectif précédent

1°) Les graphiques(inventaire)

2°)Toutes les représentations graphiques de base en statistique.

Objectif suivant :

1°) exploitation graphique.

2°)Les « fonctions » et les: principales représentations graphiques

/ 5

Les représentations graphiques et les fonctions

DOSSIER :

INVENTAIRE DES PRINCIPALES REPRESENTATIONS GRAPHIQUES des séries statistiques

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation


Généralités : Les graphiques ont un rôle prépondérant dans la communication :Ne dit -on pas qu’un bon graphique vaut mieux qu’un long discours. Encore faut -il savoir lire ou « décrypter » ce qu’il contient.. Ces graphiques sont au nombre de Il y a les graphiques de bases : Il y a ceux qui vont nous informer sur la « distribution » ( l’effectif (nombre d’individus ou éléments)par variable ou caractère) : Pour cela on utilisera soit le diagramme à bâton soit l’histogramme à partir desquels on tracera des morceaux de droites ou des morceaux de courbes pour obtenir soit des « polygones » ou des courbes. Que l’on analysera. Il y a ceux qui vont nous informer sur la « répartition » : A partir des graphiques de distribution et après des calculs (que l’on rencontrera ….) on tracera des graphiques qui nous informera sur la répartition des caractères ou variables ( notamment pour ce qui concerne les effectif et les fréquences cumulées « croissantes ou décroissantes ». Il y a les graphiques a échelle arithmétique : (qui comprend deux groupes : les « cartésiens » et les « polaires ») Il y a les graphiques à coordonnées cartésiennes : ces graphiques nous informent sur la chronologie des événements (on informe en fonction du temps……). (c’est un droite constituée de lignes brisées) . 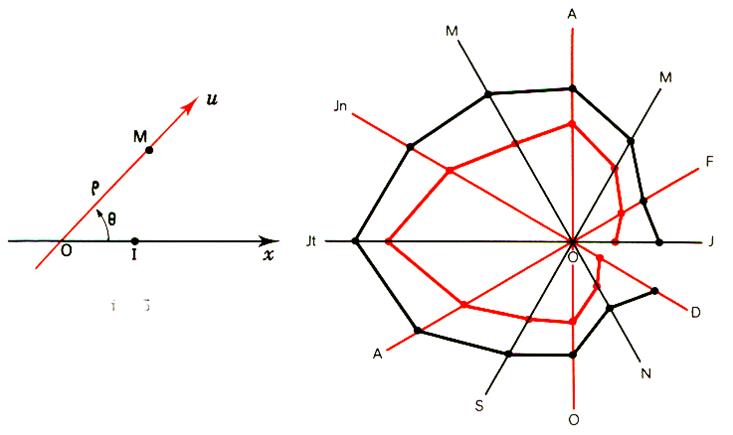Il y a les graphiques à coordonnées polaires : ( 2 types) Il a ceux qui informent sur la chronologie (les graphiques polaires) Il y a ceux qui informent sur les « fréquences… » ( ce sont les graphiques à secteurs) Il y a les graphiques à échelle NON - arithmétique : L’utilisation des graphiques à l’échelle arithmétique est limitée : risques de saturation sur les valeurs extrêmes , sur les intervalles , les échelles disproportionnées en abscisse et ordonnée , ce qui entraîne , un « effet subjectif trompeur » en cas d’étude visuelle et d’interprétation . Pour palier à ces inconvénients on a recours à des graphiques dont l’échelle est dite « logarithmique » ou « semi- logarithmique ». Ces graphiques sont utilisés pour représenter des phénomènes qui subissent des « variations importantes ».
On rencontre aussi le diagramme figuratif ( figures géométriques , personnages , animaux dont la dimension varie « proportionnellement à …..à une figure, personnage ou animal référent »)et de diagramme de GANTT. (voir exemple dans ce qui suit) .
Info. COURS

Pour donner une idée synthétique des tableaux statistiques , on utilise généralement une représentation graphique qui permet une description immédiate et complète du phénomène étudié . Liste des principales représentations graphiques :
1°) La représentation graphique dans un repère cartésien ; l’axe Ox représente les valeurs du caractère quantitatif ; l’axe Oy les valeurs des effectifs ou fréquences.
2°) La représentation en coordonnées polaires .
3°) La représentation circulaire .
4°) Le diagramme figuratif
5°) Le graphique de Gantt
Deux types de représentations graphiques sont couramment utilisées :
1° ) Les graphiques cartésiens , qui utilisent un repère formé par deux axes le plus souvent orthogonaux :
· Pour les diagrammes bâtons
· Les diagrammes en tuyaux d’ orgue
2°) Les graphiques en surface qui représentent les nombres par des surfaces dont les aires sont proportionnelles :
Deux groupes :
· Secteurs circulaires
· Histogrammes .

I ) Diagrammes cartésiens à échelles métriques

A) DIAGRAMME « BATONS » et séries a variable discrète

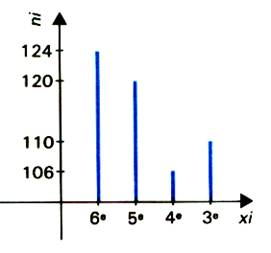
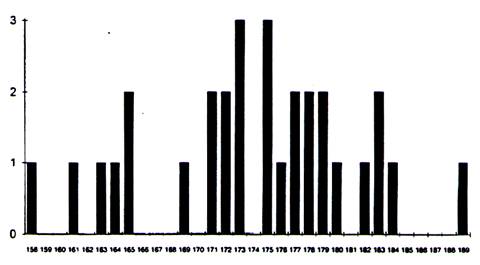
Le diagramme en bâtons est utilisé pour représenter les séries statistiques correspondant à un caractère discret .

A chaque valeur x_i de la variable on fait correspondre un segment parallèle à l’axe Oy et dont la longueur est proportionnelle à l’ effectif n_i correspondant , ou à la fréquence f_i selon qu’il s’agit d’un diagramme des effectifs ou d’un diagramme des fréquences .

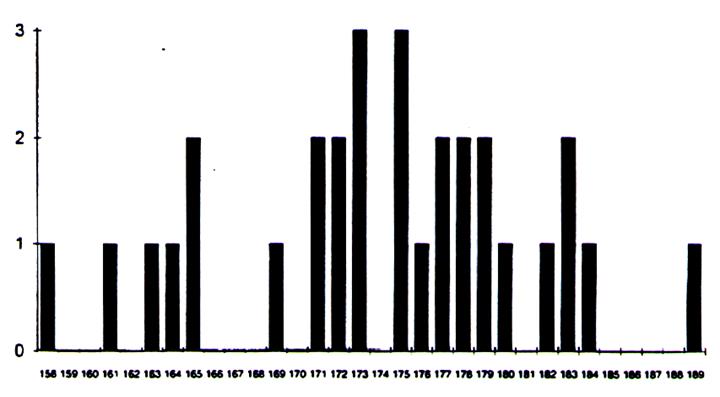
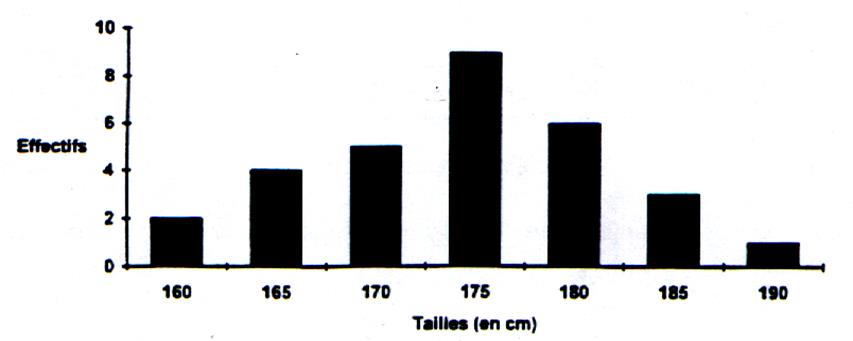
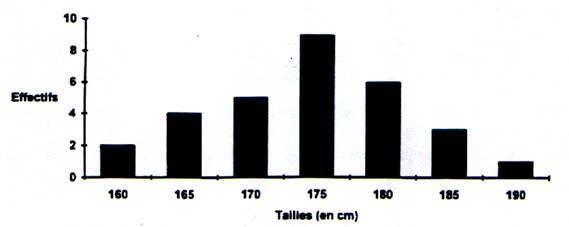
Exemple : Nous relevons les tailles en cm de 30 individus adultes , pris au hasard. A chaque individu correspondra une taille.

Après recensement des variables , nous obtenons le tableau de données suivant:

	Tailles en cm				158			159	160			161		162		163			164	165			166	167			168
	nombre				1			0	0			1		0		1			1	2			0	0			0
	Tailles en cm				169			170	171			172		173		174			175	176			177	178			179
	nombre				1			0	2			2		3		0			3	1			2	2			2
	Tailles en cm				180			181	182			183		184		185			186	187			188	189			190
	nombre				1			0	1			2		1		0			0	0			0	1			0
	Nous pouvons faire une représentation graphique , il s'agit là d’un diagramme en bâtons.
		Nombre d’individus ayant la taille correspondante

	Remarque : dans un diagramme bâton la longueur de chaque bâton est proportionnelle à l’effectif qu’il représente utre exemple :
	Répartition des élèves dans un collège



	B ) Le diagramme en tuyaux d’orgue ou HISTOGRAMME et série à variable continue : Attention : un histogramme est une représentation par une surface . L’ échelle doit être indiquée par une surface ( carré ou rectangle ) et l’ Oy ne représente aucune grandeur concrète : écrire « effectif » sur cet axe et le graduer est donc une faute grave , bien que courante et entretenue par la confusion avec un diagramme en tuyaux d’orgue. Dans le cas où la variable peut pratiquement prendre un grand nombre de valeurs , on traite la série comme si cette variable était continue . Par définition : l’histogramme et le diagramme en tuyaux d’orgue représente graphiquement une série à variable continue . Comment reconnaître un histogramme d’un diagramme en tuyaux d’orgue ?: Pour le diagramme en tuyaux d’orgue : Sur l’axe des abscisses sont marquées les extrémités des classes successives .Sur l’axe des ordonnées on marque les effectifs. Pour un histogramme : Un histogramme est constitué d’une succession de rectangles accolés l, l’aire des rectangles sont pris en compte pour l’analyse .L’ échelle doit être indiquée par une surface ( carré ou rectangle ) et l’ Oy ne représente aucune grandeur concrète a) diagramme en tuyaux d’orgue suite de l’exemple précédent : après regroupement des individus .(que noue appellerons « classe »)
	Valeurs extrêmes			158-162			163-167				168-172				173-177			178-182				183-187				188-190
	Valeurs centrales			160			165				170				175			180				185				190
	effectifs			2			4				5				9			6				3				1
	*Commentaire :* En opérant le regroupement en intervalles , nous avons constitué 7 classes. Dans chaque classe , les effectifs montrent le nombre d'événements produits (l' événement est : taille - individu). Pour pouvons obtenir un autre diagramme « bâtons ».

	Nous pouvons aussi tracer l’histogramme :
Valeurs extrêmes			158-162			163-167				168-172			173-177				178-182				183-187				188-190
Effectifs			2			4				5			9				6				3				1
Autre exemple d’histogramme

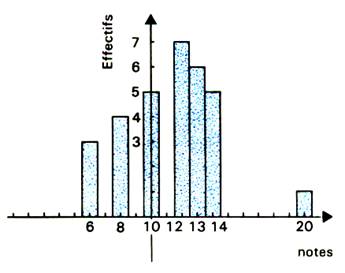
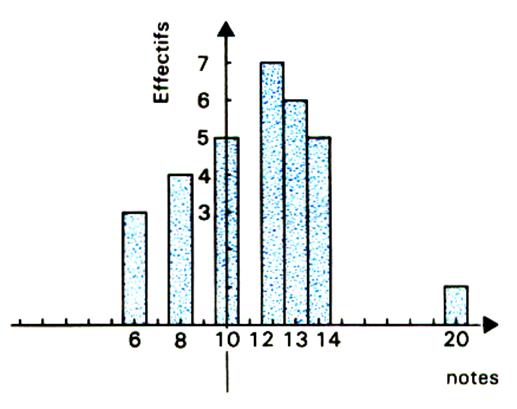
2° ligne : nombres d’élèves ( effectifs) 3° ligne : effectifs cumulés
notes	6	8	10	12	13	14	20
2°)	3	4	5	7	6	4	1
3°)	3	7	12	19	25	29	30
C ) LES POLYGONES STATISTIQUES. La ligne polygonale relie les points ( x_i; n_i ) du diagramme en bâtons.

Ce type de tracé est utilisé pour représenter les FCC et les FCD .
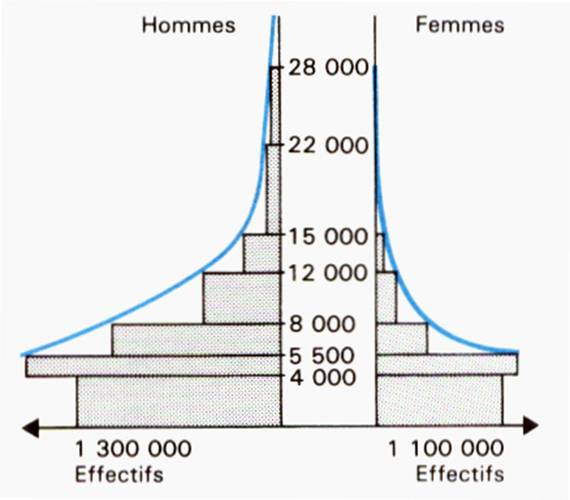
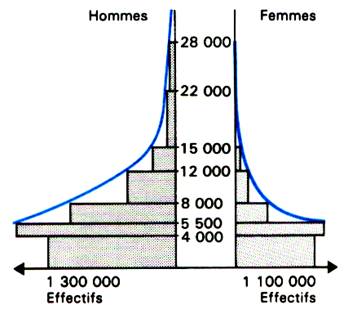
D) La pyramide
. La pyramide est obtenue par leur base de deux séries statistiques de même caractère
II ) DIAGRAMME NON CARTESIEN :
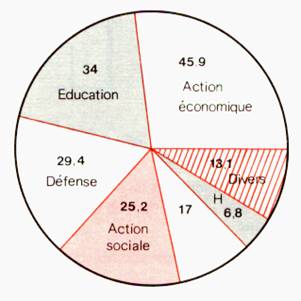
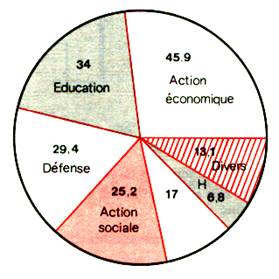
A) Les diagrammes circulaires ou « à secteur circulaire »								SOS Plus +++
Un diagramme circulaire admet pour support un disque découpé en secteurs dons les aires sont proportionnelles aux pourcentages des différents constituants de la population.

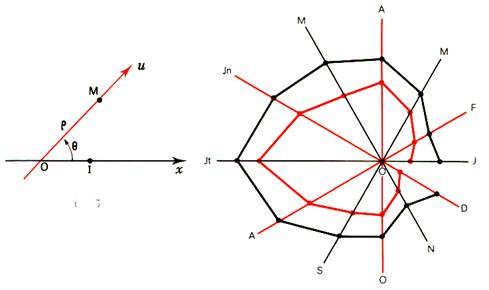
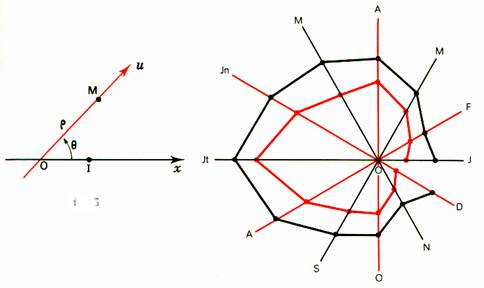
B) Les diagrammes polaires

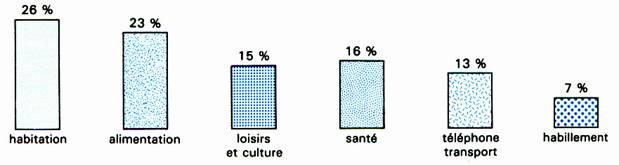
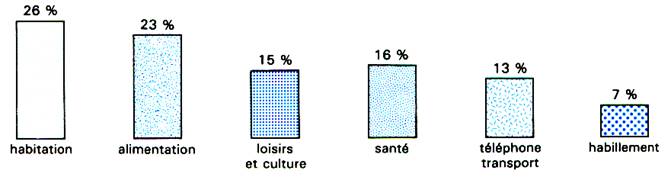
	C) DIAGRAMME FIGURATIF Exemple : la répartition moyenne des dépenses d’un ménage français en 1995

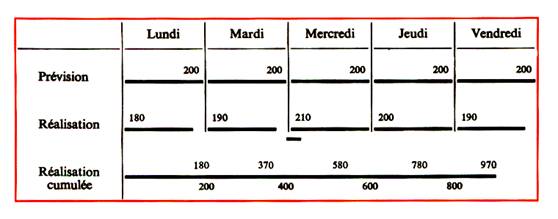
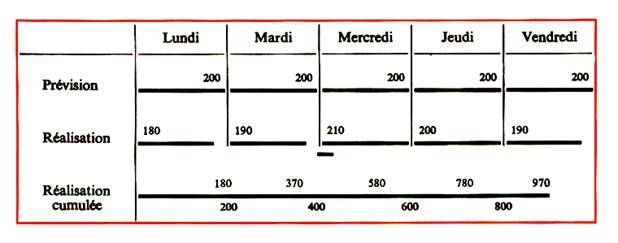
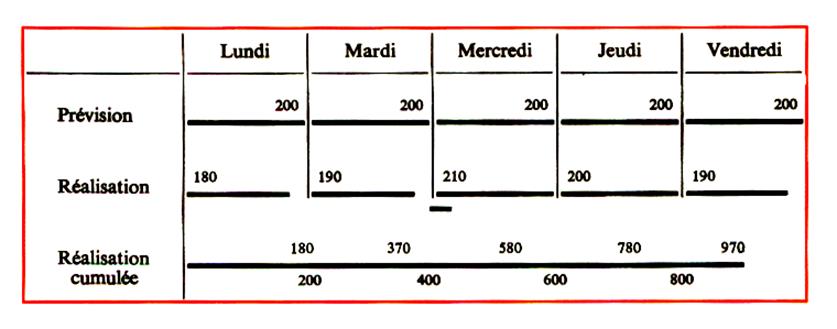
	D) GRAPHIQUE DE GANTT Le graphique de Gantt permet de comparer rapidement le rendement obtenu pendant une période donnée par une machine , une équipe d’ouvriers , .. ;et les prévisions de fabrication envisagées .

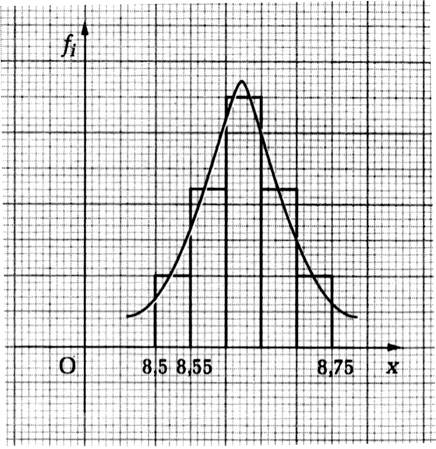
	La courbe de GAUSS