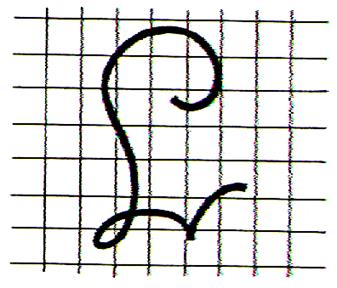|
Niv : V |
DOSSIER :
FONCTIONS LINEAIRES / Echelle |
Pré requis :
|
|
|
|
|
SOS cours |
|
Calcul numérique : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Algèbre (forme a x = b ) |
|
Environnement du dossier
|
Index |
Objectif précédent : 1°) Proportionnalité et Fonction linéaire. |
1°)Objectif suivant : Homothétie |
Tableau |
DOSSIER :
L' ECHELLE
(ou les figures semblables) Ech.
=
|
|
|
|
|
||||
|
TEST |
COURS
|
|
|||||
|
|
|
Travaux et activités : niveau VI - V Dos 136.
agrandissement et diminution Dos 137 : échelle « plan » d’une salle.
Dos 143 : échelles
et surfaces. |
|
|
|||
|
|
|
|
|||||
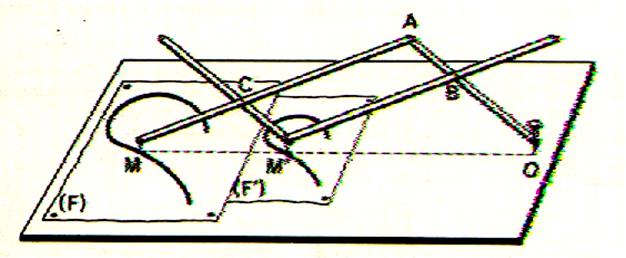
Activité :
Pour construire une maquette ,j'utilise un plan . Pour
cela j'ai mesuré à la règle plusieurs côtes
sur le plan et j'ai relevé les dimensions correspondantes sur la maquette.
|
Mesures des côtes
figurées sur le plan en cm . |
1 |
1,5 |
8,5 |
12 |
|
Mesures réelles relevées sur la maquette en cm. |
4 |
6 |
34 |
48 |
On vérifie que les deux suites de nombres sont
proportionnelles en calculant dans chaque cas la valeur du rapport.
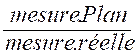
= 0,25
; 
= 0,25
; 
= 0,25 ; 
= 0,25
conclusion : "0,25" est l'échelle du plan.
L'échelle
permet d'effectuer une représentation
de la réalité avec des dimensions différentes tout en conservant les
mêmes proportions.
Dans les rapports les nombres mesurés ou relevés sont exprimés dans la même unité.
L'échelle peut s'écrire sous forme décimale : 0,25
Souvent on utilise
l' écriture sous forme d'une fraction : ou 1/4 ,ou 1 : 4
Avec l'échelle , on peut lire : 1 cm
sur le plan représente 4 cm dans la réalité .
Remarque : lorsque la valeur du rapport est
inférieur à 1 , il s'agit d'une réduction ; inversement si la valeur du rapport
est supérieur à 1 , il s'agit d'un agrandissement .
Pour l'échelle 1 : les dimensions réelles sont égales aux dimensions sur le plan.
Définitions :
Observation :
Observons deux épreuves de format différent d’une
même photo.
a)
sur les deux épreuves ,
les angles formés par deux lignes
analogues (en géométrie on dit « homologues » )
représentant les mêmes lignes réelles , sont égaux .
b)
Au contraire , les longueurs analogues sont
modifiées .
Ainsi : chaque longueur « ab »
d’une épreuve s’obtient en multipliant la longueur « AB »
correspondante de l’autre épreuve par un même nombre ou une fraction quelles
que soit ces longueurs .
Ce nombre s’appelle « échelle » , ou « rapport de
réduction » ou « rapport d’agrandissement » ou « rapport de similitude »
Echelles :
Par exemple , pour reproduire un dessin à l’échelle
½ , il faut multiplier toutes les
longueurs par ½ (ou 0,5) ; pour
reproduire un dessin à l’échelle 3 , il faut multiplier toutes les longueurs
par 3 , les angles de la figure restant inchangés.
L’échelle s’exprime aussi par un nombre décimal.
Par exemple , pour reproduire un dessin à l’échelle 2,5 , il faut multiplier
toutes les longueurs par 2,5 .
On dit aussi , par exemple , qu’un terrain est
reproduit à l’échelle de 1cm par mètre. .Cela signifie qu’une longueur vraie de
1m est représentée sur le dessin par 1 cm. Inversement , si on mesure une
longueur de 1 cm sur le dessin , c’est que la vraie longueur est 1 m .
L’échelle de réduction est égale à 1 /100 .
Il
est commode de donner l’échelle sous forme d’une fraction ou d’un nombre
décimal .
Si l’échelle est 5/7 par exemple , cela signifie
que 7 cm vrais sont représentés sur un dessin par 5 cm, que 7 m sont représentés par 5 m , , que 7 mm sont représentés par 5 mm …..
Si l’échelle est 0,5 par exemple , cela signifie
que 1 m vrai est représenté par 0,5 m ; c’est à dire 5 dm , que 1 cm est
représenté par 0,5 cm , c’est à dire 5 mm, que 1 mm est représenté par 0,5 mm ,
c’est à dire un demi millimètre.
2) Les ECHELLES USUELLES :
A) Dessin industriel :
|
Réduction |
||||||||
|
1/2 |
1 / 2,5 |
1/5 |
1/10 |
1/20 |
1/50 |
1/100 |
1/200 |
1/500 |
|
ou |
ou |
ou |
ou |
ou |
ou |
ou |
ou |
ou |
|
0,5 |
|
0,2 |
0,1 |
0,05 |
0,02 |
0,01 |
0,005 |
0,002 |
|
Agrandissement |
||||||||
|
2 |
2,5 |
5 |
10 |
20 |
50 |
100 |
Etc. |
|
B)
Cartes :
|
|
|
|
Cartes routières au 1 / 1 000 000 |
Une longueur de 1 000 000 cm sur le terrain est représentée
par 1 cm sur la carte. 1cm sur la carte représente donc 10 km sur le
terrain. |
|
Cartes routières au 1 / 100 000 |
Une longueur de 100 000 cm sur le terrain est
représentée par 1 cm sur la carte. 1cm sur la carte représente donc 1 km sur le terrain. |
|
Cartes routières au 1 / 250 000 |
Une longueur de 250 000 cm sur le terrain est
représentée par 1 cm sur la carte. 1cm sur la carte représente donc 2,5 km sur le
terrain. |
|
Cartes d’état-major au 1 / 80 000 |
Une longueur de 80 000 cm ( ou 800m) sur le
terrain est représentée par 1 cm sur la carte. 1,25 cm sur la carte représente donc 1 km sur le
terrain. |
|
Cartes ONF au 1 / 25 000 |
Une longueur de 25 000 cm ( 250 m ) sur le
terrain est représentée par 1 cm sur la carte. 1cm sur la carte représente donc 250 m sur le
terrain. |
|
Cartes ONF au 1 / 10 000 |
Une longueur de 10 000 cm ( 100 m ) sur le
terrain est représentée par 1 cm sur la carte. 1cm sur la carte représente donc 100 m sur le
terrain. Il existe des cartes aux 1/20000 et 1/5000 |
|
Les plans cadastraux : ils sont à l’ échelle 1/2500 ou 1/1000 |
Dans le premier cas , 1cm sur le plan représente 25 m sur le
terrain et dans le deuxième cas , 1 cm sur le plan représente 10 m sur le
terrain. |
3 ) ECHELLES GRAPHIQUES
a)
On se
propose par exemple de réduire les longueurs d’un dessin (mesurées)en
centimètres à l’ échelle 8 /10 .
b)
On peut tracer un segment AB ayant pour longueur 8
cm qu’on divise en 10 parties égales (Soit graphiquement voir « division
d’un segment ») simplement , en portant à partir du point A vers B , les longueurs
8 cm 
1gr
= 0,8 cm ou 8mm ; 8 cm 2gr = 16 mm ; 8 cm 3gr= 24 mm; ainsi de suite…….( ?
Calculs =SOS )
Cela revient à dire
que les divisions successives 0-1 ; 1-2 ; …. ; etc. ; représentent les longueurs : 8 cm 1gr ou 1cm1gr
C’est à dire la réduction des centimètres à
l’échelle 8 / 10 .
Par conséquent , si une longueur à réduire mesure 6
cm , on reportera sur la réduction la distance
0-6 de l’échelle .
|
|
|
On complète l’échelle en prolongeant AB jusqu’en C de façon que AC
(appelé « talon ») égale la division 0-1 de l’échelle , c’est à
dire les 8/10 d’un centimètre .On partage le talon en 10 parties égales .
Chacune de ces parties représente donc les 8/10 d’un millimètre. Pour reporter , par exemple, la réduction , la réduction de 6,8 cm ,
poser une pointe de compas en « P » et l’autre en « Q » ,
sur le talon en « 8 ». |
|
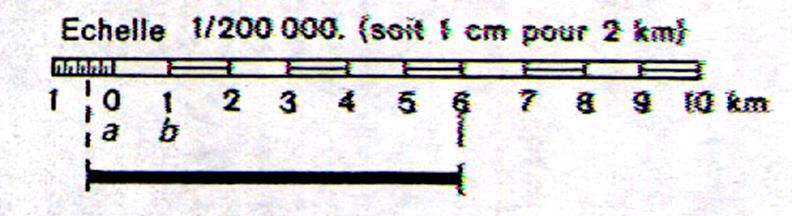
Echelle graphique 1/200 000 |
|
A propos d ‘ agrandissement ou de
réduction ou « vraie
grandeur »
1 ) nous
faisons un agrandissement , si le
rapport « Dimension du
plan » (notée : Dp) sur
« Dimension réelle » (notée : Dr) est supérieure à 1
(traduction
mathématique : si 
> 1 alors
« agrandissement »)
2 ) nous faisons une réduction , si le rapport Dp sur
Dr est inférieure à 1
(traduction
mathématique : si < 1 alors
« réduction »)
3 ) nous faisons une représentation en vraie
grandeur si le rapport Dp sur Dr est égal
à 1
(traduction
mathématique : si = 1 alors «vraie
grandeur »)
|
Exemples de la diminution ou de l’ agrandissement
. |
|
Sens de lecture ® diminution
|
|
|
|
|
|
(sens de lecture
) ¬ agrandissement |
|
4 ) INSTRUMENTS ET METHODES DE TRACE.
|
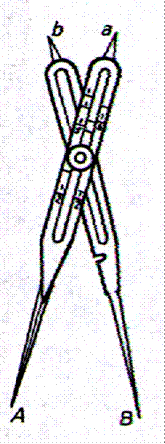
Compas de réduction (compas à pointes sèches : pointes en
métal) |
|
|
En O est une vis qui peut se déplacer le long des branches évidées du
compas .On place le trait de repère « r » en face de l’échelle de
réduction désirée et qui est gravée sur une branche .On serre la vis .Le
dispositif qui est en « O » permet de faire pivoter le compas sans
toucher à la vis. La réduction d’une longueur « AB » est « A’B’ »
.On utilise alors le compas (sans toucher à la vis) autant de fois qu’il y a
de longueurs comme « AB » à réduire. Remarquez que si
« A’B’ » est la longueur à reproduire , « AB » est son
agrandissement. |
|
|
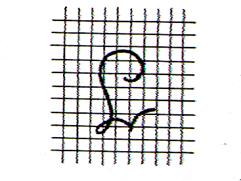
Méthode des « carreaux » |
Voir « quadrillage :
SOS cours » |
|
|
Elle convient pour les réductions ou les
agrandissements de dessins à lignes irrégulières. |
||
|
|
|
|
|
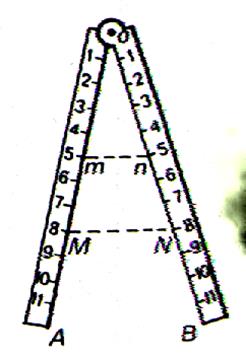
Le Compas de proportion |
|
|
Deux branches identiquement graduées peuvent
pivoter autour du point « O ». Si on veut réduire une longueur MN à l’échelle 5/8
, par exemple , placer le compas comme l’indique la figure . « mn »
est la longueur réduite. |
|
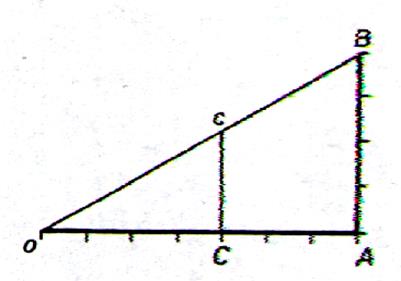
Angle de réduction |
|
|
Par exemple ,pour réduire des longueurs à l’échelle 4/7 , tracer sur
du papier millimétré OA = 7 cm , AB = 4
cm . Tracer OB . Puis porter la longueur à réduire comme Oc ; Cc est la
longueur cherchée . |
|
Se souvenir que « l’échelle » est le rapport ( Division )de la distance entre
deux points sur le plan (distance plan ) sur la distance réelle qui sépare des deux points (distance
réelle).
Les distances sont
,obligatoirement , exprimées dans la même unité de longueurs. (tout en cm
,en dm , en m ;........) On dit que ce sont des grandeurs.
Rappel :
On appelle « grandeur » un nombre associé à une unité de mesure.
L’échelle est un nombre. (elle n’ a pas d’unité
)
Ce
nombre se présente (peut se présenter )sous 4 formes :
ce
peut être un nombre entier :
exemple : échelle : 2 (on multiplie les dimensions réelles par
deux)
exemple :
échelle : 1 (on reproduit la pièce a ses dimensions
réelles) on dit aussi « reproduire en vraie grandeur » , le
rapport est alors de 1/1
ce
peut être
un nombre décimal :
échelle : 0,5 (en dessin
industriel)
ce peut être ou une fraction :
a) cette
fraction est peut être exprimée sous sa
forme irréductible : échelle 2/ 3
b) ,
ou sous sa forme de fraction de numérateur égal à 1 :
Exemples
·
Modèles
réduits : 1 / 30
· cartes militaires : à l ’ échelle 
; 
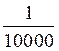; ou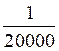 
;
· cartes routières :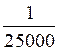 
;
;
;
;
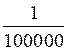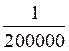· carte de l’Europe au 1/ 3 700 000
(certaines
fractions ont peuvent être remplacées par leur valeur décimale):
|
Fraction représentant un nombre
décimal : |
|
Attention :
1/ 3 700 000 n’a pas de représentant décimal.
Si l’on effectue la division , on
trouve : 1/ 3 700 000 »
0,000000 27027027
CALCULS
3
types d’exercices peuvent être demandés : ( 3 niveaux)
Niveau I :
Rechercher l’échelle en
fonction de la dimension du plan et de
la dimension réelle.
Niveau II
Rechercher la dimension du plan en fonction
de l’échelle et de la dimension réelle.
Niveau III
Rechercher la dimension
réelle en fonction de l’échelle et la
dimension sur le plan.
Quelque soit le
niveau de difficulté :
Il faut connaître et mettre la relation précédente sous forme d
‘équation mathématique :
Ech. =
ce qui donne en abrégé :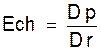 
En Résumé ,
ON retiendra que pour traiter un problème sur les échelles
on devra appliquer la procédure suivante:
Procédure :
1. Poser la relation mathématique dans laquelle intervient
le mot « échelle ».
2. Identifier dans l’énoncé
Dp et Dr .
3. Convertir dans la même unité .
4. Remplacer dans la relation mathématique les lettres par
les nombres connues.
5. Effectuer le calcul.
6. Rendre compte , en fonction des exigences.
(si
l’on ne précise rien donner la valeur sous forme de nombre décimal ou entier
,si l’opération ne « tombe » pas juste laisser le résultat sous forme de fraction
irréductible.
(dans le cas
possible donner le résultat sous forme de fraction de numérateur égal à 1 .)
Exemple : Niveau I :
Rechercher l’échelle en fonction de la dimension du plan et de la dimension
réelle.
on
demande de rechercher la valeur de l’échelle en fonction de Dp et Dr . ( On dit
aussi détermination de l’échelle )
Exercice:
Enoncé de
l’exercice : « 3,8
cm » sur une carte représente « 380 m » sur le terrain, quelle est la valeur de
l’échelle ?
CORRIGE
(en utilisant la procédure énoncée ci dessus !)
1 ) Poser la relation mathématique dans laquelle
intervient le mot « échelle ».
: Ech. =
2 ) Identifier dans
l’énoncé Dp et Dr .
3.8cm sur une carte : Dp
380 m sur le terrain : Dr
3 ) Convertir dans la même
unité .
Dp = 3.8 cm ; Dr
= 38 000cm
4 ) Remplacer dans la relation mathématique les lettres par les
nombres connues.
Si :
Ech. =
; : Ech. =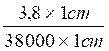
5 )
Effectuer le calcul.
Voir
Objectif puissance 3 ; sciences
= 
= 
=
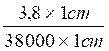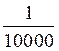
on peut aussi faire la division:
3,8 : 38000 = 0.0001
6 )
Rendre compte , en fonction des exigences.
(si l’on ne précise rien donner la valeur
sous forme de nombre décimal ou entier ,si l’opération ne « tombe »
pas juste laisser le résultat sous forme
de fraction irréductible.
(dans le cas possible donner le résultat
sous forme de fraction de numérateur égal à 1 .)
La valeur de l’échelle utilisée pour effectuer la carte
est : Echelle = 1 /10000ième
>>>>>>>>Voir
les travaux auto formatifs .