Module : Géométrie .		DOSSIER : 142 - 143
LOGICIEL warmaths ; Pour Aide et Formation Individualisée ; REMEDIATION mise à /NIVEAU : niveau VI
Info conseils et consignes.	TRAVAUX NORMATIFS PRIMAIRE / COLLEGE / Lycée. Prof – Tecno - , et Géné. Matière : MATHEMATIQUES. Niveau VI		.PB : niveau +++
ECHELLES (calculs) et SURFACES .
INFO COURS : @ cours
Voir @ dossier 136 et @ dossier 137
TRAVAUX CONTROLE
Doc WR
Les questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours .
TRAVAUX : EVALUATION
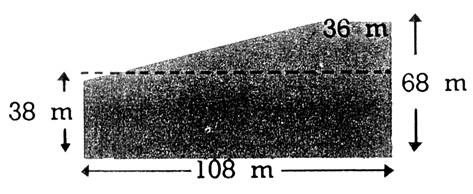
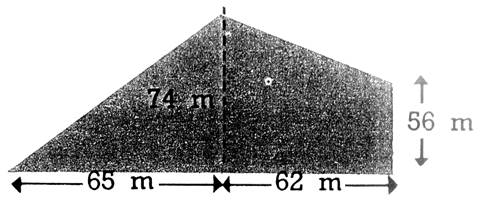
1. Calculez la surface en hectares de chacun des terrains représentés ci-dessous. « A »
« B » La hauteur = 74 m
2. Calculez la dimension inconnue, marquée par un point d’interrogation
« A » Surface totale :3 568 m²
« B » Surface totale : 6 496 m²
3. Sur un plan à l’échelle 1:2000, un pré a la forme d’un rectangle de 5,6 cm de long et 3,2 cm de large. Calculez de deux façons son périmètre. 4. Le périmètre d’un pré rectangulaire mesure 12,6 cm sur un plan à l’échelle 1:2500. La largeur de ce pré est la moitié de sa longueur. Quelle est sa surface, en hectares? 5. Sur un plan à l’échelle 1 : 1 000, un verger est représenté par un rectangle de 6 cm sur 4,5 cm. a) Quelles sont ses dimensions réelles ? b) Quelle est sa surface ? Pour calculer celle-ci, un élève a multiplié la surface du plan (6´ 4,5 = 27 cm^2) par 1 000. Sa réponse est-elle exacte ? Par combien aurait-il dû multiplier 27 cm^2pour trouver la réponse exacte ?
Info : Retenez Pour calculer la surface d’un terrain à partir des dimensions sur un plan, il faut d’abord calculer les dimensions réelles, et non la surface sur le plan.
6. Un champ rectangulaire mesure 6,5 cm de long sur un plan à l’échelle 1 : 2 000. A 375 € e l’are, ce champ a été vendu 3 8025 €. Quelle est sa surface, sa largeur réelle, sa largeur sur le plan ?
CALCUL MENTAL. Diviser par 20, 200 ... on prend la moitié, qu’on divise ensuite par 10,100 7. Sur un plan à l’échelle 1 :20, dites par quelle longueur on représente 4 m; 12 m; 10 m; 7 m; 3 m; 4,80 m; 8,20 m; 6,40 m; 5,60 m; 9,20 m. 8. Sur un plan à l’échelle 1 :2 000, dites par quelle longueur on représente 30 m; 80 m; 120 m; 48 m; 142 m; 64 m; 26 m; 52 m; 34 m; 74 m. Diviser par 50, 500 ... on divise par 100, 1 000 ... et on double le résultat. 9. Sur un plan à l’échelle 1 : 500, dites par quelle longueur on représente 15 m; 24 m; 30 m; 45 m; 8 m; 36 m; 55 m; 32,5 m; 64 m; 27,5 m. 10 Sur un plan à l’échelle 1 : 50, dites par quelle longueur on représente : 20m; 8m; l2m; 3 m; 6 m; 1 4 m; 28m; 4,2m; 3,6m; 5,4m. Fin de ce calcul mental.
SITUATIONS PROBLEMES.
11 Un champ rectangulaire mesure 37 m de large et 122,5 m de long. On y trace une route nouvelle de 9,5 m de large, qui le coupe en deux parcelles dont l’une est un carré. a) Faites le dessin du champ et de la route. b) Calculez la surface des 2 parcelles qui restent. 12. La figure ci-dessous représente un champ à l’échelle 1 : 2 500. Une route de 15 m de large, nouvellement construite, la coupe perpendiculairement aux bases, le divisant ainsi en un rectangle de 20 m de large, et un trapèze. Dimensions : lire : 25 mm ; 32 mm ; 46 mm a) Reproduisez la figure en y dessinant la route à sa place exacte. b) Quelle indemnité, à 2,50 € le m², le propriétaire du champ recevra-t-il pour la surface qu’on lui enlève ? c) Calculez la surface de chacune des deux parties restantes du champ. 13. Tracez un rectangle dont la largeur est le tiers de la longueur, a) Combien de fois la largeur est-elle contenue dans le périmètre ? Quelle fraction en est-elle ? b) Calculez la surface de ce rectangle si son périmètre mesure 120 m. 14. Un terrain rectangulaire mesure 266 m de périmètre. Sa largeur mesure 35 m de moins que sa longueur, a) Quelles sont ses dimensions ? 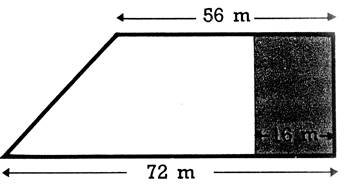b) On le partage en deux rectangles, par une parallèle au petit côté, la surface d’un rectangle étant double de la surface de l’autre faites le dessin; calculez la surface et les dimensions de chaque parcelle. 15. La partie coloriée du terrain à bâtir repré senté ci-dessous a été vendue 697,2 € a raison de 105 € l’are. (La bande grise mesure 16 m) a) Quelle est sa surface ? b) Calculez, en vous aidant de cette surface, la hauteur du trapèze. c) Quelle est la surface restante ? 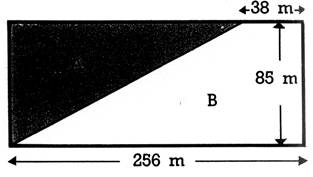16. La construction d’un terrain d’aviation entraîne l’expropriation de la partie « A » grisée , du champ rectangulaire ci-contre, a) Quelle est la forme de chacune des deux parcelles du terrain partagé ? b) Quelle est la surface de chacune d’elles ? c) Vérifiez en recomposant la surface du terrain rectangulaire. 17. Une pièce de terre rectangulaire de 320 m de long et 65 m de large a produit une récolte de blé qui, à 43,5 € le quintal, a rapporté 2 262 €. a) Quelle est la surface du champ ? b) Quel est le poids de la récolte ? c) Quel a été le rendement de cette pièce de terre, en quintaux par hectare ? 18. On achète un terrain carré pour la•somme de 37 903,15 € . On l’entoure d’une clôture qui revient à 1198,88 € à raison de 2,36 € le mètre. Quel était le prix du mètre carré de terrain ?