SUITE : fiche 6 et ………  « 9 »

Classe de troisième

Applications affines.

Voir programme classe de troisième.

III )  LECON  Suite  sur Les applications affines   .( classe 3^ème)

Les représentations graphiques.

Fiche 1 : Définition d’une application affine.

Fiche 2 : Représentation graphique d’une application affine.

Fiche 3 : Le bon choix.

Fiche 4 : Détermination d’une application affine.

Fiche 5 : Déplacement a vitesse constante.

Fiche 6 : Représentation graphique  du déplacement d’un cycliste.

Fiche 7 : Résolution graphique d’un problème d’algèbre.

Fiche 8 :  Résolution d’un problème de géométrique.

Fiche 9 : Situations problèmes types.

Les applications affines   .( classe 3^ème)

Retour aux fiches de 1 à 5.

Fiche 6 : Représentation graphique  du déplacement d’un cycliste.

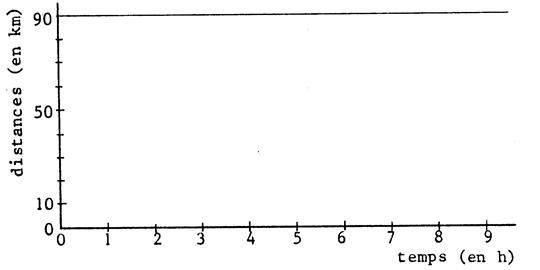
Igor fait l’ascension du Mont Chauve à bicyclette.

Du bas de la côte au sommet , il y a 90 km . La pente est régulière.

Il gravit cette pente à la vitesse constante de 18 km/h .

Il se repose  « 1h » puis il redescend  à la vitesse constante de « 30 km/h »

1°) Sachant que « Igor » est parti à midi ( c'est-à-dire à « 0 h » de l’après midi .

A quelle heure arrivera-t-il au sommet ? ……………………………………………………

2°) A quelle heure sera-t-il de retour en bas ? ………………………………………………

3°) Vous allez faire la représentation graphique de déplacement du cycliste.

C'est-à-dire , vous allez représenter graphiquement en fonction du temps , la distance du cycliste au point de départ.

Sur l’axe des  abscisses on a porté  le temps ( en h).

L’origine des temps est « 0h ».

            Sur l’axe des ordonnées , on a porté les distances  ( en km).

        L’origine est le bas de la côte.
le sommet  a pour ordonnée … 90 ………

Phase  « Montée »  :

Au départ , le point représentatif  du cycliste a pour coordonnées  ( ….. ; ……)  .

Au sommet , le point représentatif a pour  coordonnées ().

Placez ces points .

Puisque la vitesse est constante  , le déplacement du cycliste est une application affine du temps ;

La représentation graphique est donc une portion de droite :

 C’est le segment limité par les deux points que vous venez de placer . Tracez-le.

·       Déterminons l’équation de la droite correspondante.

Puisqu’elle passe par l’origine , elle a une équation de la forme «   ».

Comme elle passe par le point de coordonnées (  ) alors «   »     d’où   «   »

L’équation de la droite est alors : «   ».

·       Cette droite est la représentation graphique de l’application linéaire :       et vous remarquez que son coefficient est égal à la . ……vitesse constante ……………………….

Phase « repos ».

Au début du repos , le point représentatif correspondant a pour coordonnées   ( …. ;…..) ; ().

A la fin du repos , « 1 h » plus tard , Igor est toujours à 90 km de « A ».

Le point représentatif a  donc  pour  coordonnées ( 6 ; 90 ) . Placez ce point .

La représentation graphique correspond au repos est donc le segment joignant ces deux points . Tracez – le .

·       L’équation de la droite correspondante est «   »

Cette droite est la représentation graphique de l’ application affine :     

Phase « Descente » .

Au départ de la descente , le point représentatif a pour coordonnées   ( …6. ; …90…)

A l’arrivée , le point représentatif a pour coordonnées  ( …9 .. ; …0….). Placez –le .

Puisque la vitesse de descente est constante , la représentation graphique est une portion de droite : c’est le segment joignant ces deux points. Tracez-le.

·       Déterminons l’équation de la droite correspondante.

Elle est de la forme  «   »  et elle passe par les points de coordonnées  ( 6 ; 9 )    et  ( 9 ; 0 ) .

A vous de déterminer cette équation comme vous l’avez (surement ) fait dans l’étude des «  fiches .++équations de droites dans +++ »  .

Cette droite est la représentation graphique de l’application affine :    

Et vous remarquez que le coefficient «   » est l’opposé de la  ………………………………………

Fiche 7 : Résolution graphique d’un problème d’algèbre.

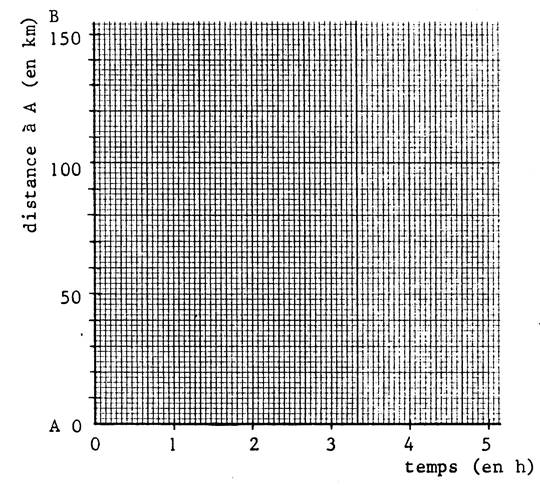
Deux villes « A » et « B » sont distant de « 150 km ».

Rémi part de « A » à bicyclette à «  0 h »  et va en « B » à la vitesse de « 30 km /h » .      ( autre notation : «  30  » )

Pierre part de « A » en automobile  à  «  0h 40 min » et va vers « B » à la vitesse de « 90 km /h »

IL roule pendant « 40 min » puis il s’arrête deux heures.

Il reprend ensuite sa route jusqu’en « B » à la même vitesse ( 90 Km/h).

Léon part de « B » en camion à « 1h 30 min » et va en « A » à la vitesse  « 60 km /h »

On vous demande :

1°) Faites la représentation graphique du déplacement de ces trois véhicules.

2°) Après avoir lu sur le graphique puis vérifié par le calcul , complétez :

·       Durée du trajet de Rémi en bicyclette :……………………………… ; Heure d’arrivée en « B » : ………………………

·       Durée du trajet de Joël  en automobile  :……………………………… ; Heure d’arrivée en « B » : ………………………

·       Durée du trajet de Léon  en camion  :……………………………… ; Heure d’arrivée en « A » : ………………………

3°) Lisez sur le graphique  « heure » et « lieu » de rencontre des véhicules .

Complétez le tableau ci-dessous :

Véhicules

Heure

Distance de « A »

Rémi et  Léon

Joël et Léon

4°) On désigne par . 

-         «  »   la distance de Rémi à la ville « A » en fonction du temps.

-        «  » ; «  »   ; «  »      les  distances  respectives de  Joël  à la ville « A » en fonction du temps dans les trois phases de son mouvement .

-        «  »   la distance de Léon à la ville « A » en fonction de temps .

Après avoir fais vos calculs au  brouillon , complétez : 

«  »  

«  » 

«  »  

«  »     

«  »  

5°) Retrouvez par le calcul , l’heure et le lieu de rencontre des véhicules .

Fiche 8 :  Résolution d’un problème de géométrique.

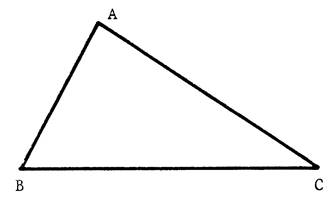
« ABC » est un triangle tel que  , en cm , « AB = 15 » ; « BC = 27 » ; «  CA = 24 »

« M » est un point quelconque du segment  .

On désignera « AM »  par «  » .

Puisque « AB = 15 » ; alors

On trace « M » la parallèle à (BC) qui coupe   en  « N ».

On trace  par  « N» la parallèle à (AB) qui coupe   en  « P ».

1°) Calculez en fonction de  « x » , « MN »  et  « AN » .   ( voir cours n°°°°. …..)

2°) Quelle est la nature du quadrilatère «  MNPE » ?    ( justifiez votre réponse)

3°) Exprimez en fonction de «  » le périmètre «  »  du quadrilatère « MNPE » .

4°) Exprimez en fonction de «  » le périmètre «  »  du triangle  « NPC » .

5°) « y » et « z »  sont des fonctions de « x ».  Sont-elles des applications affines ?. ……………………………………… 

Faîtes ci-dessous leur représentation graphique.

6°) Il existe une valeur  de « » pour laquelle le périmètre de «  MNPB » est égal à celui de « NPC ».

Déterminez cette valeur  ( ou une valeur approchée ) par simple lecture sur le graphique . Vous trouvez :  «   »

Vérifiez en calculant «  » et «  » pour la valeur de «  » que vous venez de trouver .

7°) Retrouvez cette valeur de «  » par le calcul ( résolvez l’équation «   » )

Fiche 9 :  5  Situations problèmes types

( il n’existe pas encore de corrigé)

Problème 1 : (d’après un sujet de brevet )

Les longueurs sont exprimées en « cm » et les aires en « cm² ».

« ABC » est un triangle rectangle en « A » tel que « AB = 8 » et « AC = 6 »

« D » est un point du segment    tel que  «  AD = 2 ».

« M » est un point quelconque du segment . On pose  «  x = AM ».  

La parallèle à ( AC)  passant par “M” coupe  ( BC ) en   « N ».

La parallèle à ( AB ) passant par « N » coupe  ( AC)  en « P ».

Questions :

1°) Calculez l’aire du triangle « ABC ».

2°) Quelle est la nature du quadrilatère « AMNP » ?     en déduire « PN » .

3°) Exprimez en fonction de « » l’aire du triangle  « NCD » .  ON la désignera par «   ».

4°) Exprimer en fonction de «  » l’aire du quadrilatère « NDAB » . On la désignera par «  ».

5°) Représenter graphiquement les applications affines  «  » et « » . (  )

6°) A l’aide du graphique, déterminez la valeur de « x » pour laquelle les aires  du triangle « NCD » et du quadrilatère  «  NDAB » sont égales. Quelle est cette aire ?

7°)Retrouvez par le calcul les résultats de la question «  6°) »

Problème 2 :

Une bibliothèque propose trois formules de prêt de livres :

-        Formule « A » : Payer 5 € par livre emprunté.

-        Formule  « B » : Prendre une carte demi-tarif à  20 € par an et payer en plus  2,5 €  par livre emprunté.

-        Formule « C » : Payer un abonnement de  60 € par an .  ( sans limite  de livres  empruntés)

Questions :

1°) En désignant par «  » le nombres de livres empruntés en un an , exprimez en fonction de « » les dépenses annuelles  «   » ; «  » ; «  » correspondant aux formules « A » ; « B » ; « C ».

2°) Faîtes la représentation graphique des applications affines correspondantes.

3°) En utilisant le graphique , déterminez, suivant le nombre de livres empruntés la formule la plus avantageuse.

4°) Retrouvez par le calcul les résultats de la troisième question.

Problème 3 :

La distance de Paris à Lyon par le train est de 500 km.

Un premier train par de Paris à « 1 h » et roule vers Lyon à la vitesse de « 75 km/h ».

Un deuxième train part   de  Lyon à  « 3 h » et roule vers Paris  à la vitesse de « 100 km/h ».

Questions :

1°) En désignant par « » le temps en «  » , exprimez en fonction de «  » la distance «   » du premier train à Paris et la distance «  » du deuxième train à  Paris.  ( voir la fiche 5 ) .

2°) Faire la représentation graphique correspondante.

  Sur l’axe des abscisses , vous portez  le temps (t)  en « h » . L’origine  des temps est « 0 h ».

  Sur l’axe des ordonnées , vous portez les distances ( en km) .  L’origine des espaces est Pais  au « km 0 » , Lyon est au « km  500 ».

3°) Lire sur le graphique l’heure du croisement des  « 23 trains et leur distance à Paris.

4°) Retrouvez par le calcul les résultats de la question « 3°) »

Problème 4 :

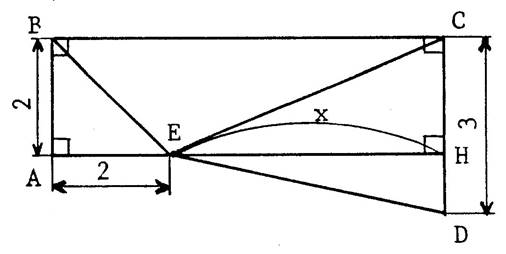
« ABC » est un triangle  tel que  ( en cm) , «  AB = 8 »  , « BC = 10 » , « CA = 9 ».

« E » est un point de . Par « E » on mène la parallèle à ( AB) qui coupe ( AC ) en « F ».

Questions :

1°) En appelant «  » la distance de « E » à « C » , exprimez en fonction de «  » la périmètre : «  » du triangle « EFC » et le périmètre  «   » du trapèze « ABEF ».

2°) Faîtes la représentation graphique de «   »  et de «  »

3°) A l’aide du graphique , déterminez la valeur de « x » pour laquelle les deux périmètres sont égaux. Quel est ce périmètre ?

4°) Retrouvez par le calcul les résultats de la question « 3°) »

Problème 5 :

On considère la figure ci-dessous :

AB = 2 cm ; AE = 2 cm , CD = 3 cm , EF =   cm.

On se propose de comparer les aires des trois triangles : « AEB » , « BEC » et « CED » quand la longueur «  » varie.

Questions :

1°) Calculez « BC » en fonction de « x ».

Calculez en fonction de « x » les aires : «  » ; «  »   ; «  »  des triangles : « AEB » , « BEC » et « CED ».

2°) Faîtes les représentations graphiques   «  » , «  » , «  »  des fonctions affines : «  » ; «  »   ; «  » 

3°) Calculez les coordonnées  des points d’intersection des droites «  » et  «  » et   «  » et  «  »

4°) Utilisez les représentations graphiques pour répondre aux question suivantes :

Pour quelle valeur de «  » a-t-on  «    » ? .  Que vaut alors cette aire ?

Peut-on avoir  «       » ?   Justifiez la réponse .

5°) Pour  «  »  ranger par ordre croissant les trois aires . Justifiez la réponse .

6°) Comparez également ces trois aires pour  «  » . Justifiez la réponse.

Terminé le 28/12/15