|
|
|
Classe de troisième |
|
|
|
|
|
|
|
|
|
|
Applications
affines. |
|||
|
|
|
|
||
|
DOC :
formation individualisée soutien en ligne. |
DOC :
livre Elève .Cours interactifs - et travaux + corrigés. |
|
¥ |
|
|
¥ |
|
|
·
La
fonction linéaire
(généralement traité avant la fonction affine) ·
La fonction linéaire est
une forme dérivée de la fonction affine : y = m x + p ( avec
« p = 0 » |
¥ |
|
¥ |
II ) ENVIRONNEMENT du dossier :
AVANT :
|
APRES : 1°) Les
droites croissante ; décroissante,.. 2°)le parallélisme et la
perpendicularité Travaux : 3°) Fonction affine
et application. |
Complément d’Info :
Fonction
affine : présentation |
|
|
III ) LECON
n° 24 Les
applications affines .( classe 3ème) |
|
|
|
|
|
|
|
Fiche
1 : Définition d’une application affine. |
|
|
|
Fiche
2 : Représentation graphique d’une application affine. |
|
|
|
Fiche
3 : Le bon choix. |
|
|
|
Fiche
4 : Détermination d’une application affine. |
|
|
|
Fiche
5 : Déplacement a vitesse constante. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV) INFORMATIONS « formation leçon » :
|
Travaux auto - formation. |
|
|
Corrigé des
travaux auto - formation. |
||||
|
|
|||||||
|
|
Les applications affines .( classe 3ème) |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Fiche
1 : Définition d’une application affine |
|
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Exemple
1 :Le calcul du prix d’une course en taxi se
fait de la manière suivante : On
ajoute une somme fixe appelée « prise en charge » à une somme
proportionnelle au nombre de kilomètres parcourus. Sachant
que la prise en charge est « 10 € » et le prix du km « 4 € », exprimons
, en fonction du nombre de kilomètres , le prix de la course. |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Pour
une course de « 3 km » , le prix ( en
€ » est « Pour
une course de « 7 km » , le prix ( en
€ » est « Pour
une course de « |
|
|||||||||||||||||||||||||
|
|
«
|
|
|||||||||||||||||||||||||
|
|
En
désignant par « p » ce procédé , on écrit schématiquement :
Ce qui
signifie : Par le procédé « Exemple : Par le
procédé « |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Exemple 2 : Un
réservoir contient « On
le vide par l’intermédiaire d’un
robinet dont le débit est de « En
désignant « On la désigne par « ( On considérera
que l’on commence à vider le réservoir à l’instant « |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
La
quantité d’eau écoulée est proportionnelle au temps .
(le débit est de « Au
bout de une ( 1 ) minute , il s’est écoulé Au
bout de ( 8 ) minutes , il s’est écoulé Au
bout de « On
a alors « |
|
|||||||||||||||||||||||||
|
|
Comme
dans l’exemple 1 , à tout nombre « |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
De
tels procédés sont appelés « fonctions affines » ou
« applications affines » . |
|
|||||||||||||||||||||||||
|
|
A
retenir : Etant
donné deux nombres « |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
« |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Dans
l’exemple 1 ,
|
|
|||||||||||||||||||||||||
|
|
Dans
l’exemple 2 ,
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Remarque
1 : Toute application linéaire est une application affine dans laquelle
« Remarque
2 : Dans
le cas où « |
|
|||||||||||||||||||||||||
|
|
Activité :
« |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
oui |
oui |
non |
oui |
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Fiche
2 : Représentation graphique d’une application affine |
|
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
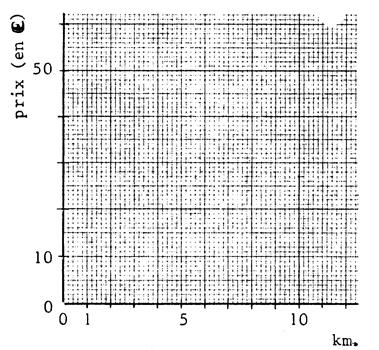
Nous
reprenons l’exemple de la fiche 1 : « le prix d’une course de
taxi » et faisons la représentation graphique du prix en fonction du
nombre de « km ». |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Nous
avons choisi deux axes de coordonnées , la représentation graphique est
constituée par tous les points dont l’abscisse « x » est un nombre
de kilomètres et dont « y »
est le prix de la course correspondante. Pour
effectuer ce graphique nous avons choisi quelques points . Complétez
le tableau ci- dessus :
|
|
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
1 |
2,5 |
4,2 |
6 |
7,6 |
8,5 |
10 |
|
|
||||||||||||||||
|
|
|
|
14 |
20 |
26,8 |
34 |
40,4 |
44 |
50 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Placez
les points . Vous constatez qu’ils sont alignés. Tracez
la droite passant par ces points. |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Ce
que vous avez constaté , nous allons le démontrer. |
|
|||||||||||||||||||||||||
|
|
Considérons l’application affine Tout
point de la représentation graphique de « « y »
et « x » sont donc liés par la relation « Or , vous
savez ( voir
fiche 2 : fiche équations de droites) que l’ensemble des points
dont les coordonnées ( x ; y ) vérifient « Donc , les points
de la représentation graphique sont bien alignés. |
|
|||||||||||||||||||||||||
|
|
Remarque : Dans le cas du taxi ,
les points de la droite ne conviennent pas tous : en effet
« x » , le nombre de « km » est forcément positif , et il
ne peut pas être trop grand. |
|
|||||||||||||||||||||||||
|
|
· Ce que l’on
vient de dire pour l’application |
|
|||||||||||||||||||||||||
|
|
A
retenir : Etant
donné deux nombres « mm et
« p » , la représentation graphique
de l’application affine |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
La
représentation graphique cherchée est
une portion de la représentation graphique de l’application affine
C’est
donc une portion de la droite d’équation |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
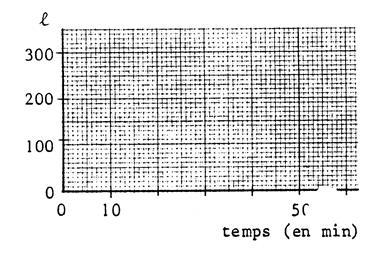
Elle
est limitée par les deux points
suivants. Au
départ : pour « Le
point de coordonnée (
0 ; 300 ) est donc un point
limite. Le
bassin est vide quand « La
valeur correspondante de « L’autre
point limite a donc pour coordonnées : ( 50 ; 0 ) Placez
ces deux points et tracez le segment les joignant : C’est
la représentation graphique cherchée. |
|
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Fiche
3 : Le bon choix |
|
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
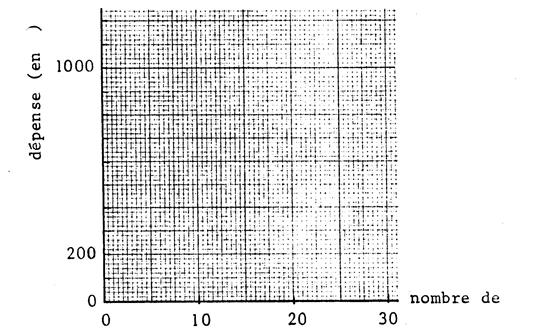
Un
club de foot professionnel propose à ses supporters 2 options : Option
« A » : Prix de la place « 40 € » Option
« B » : Abonnement de « 300 € » par an et prix de la place « 20
€ ». |
|
|||||||||||||||||||||||||
|
|
1°)
Calculez la dépense annuelle dans les cas suivants : |
|
|||||||||||||||||||||||||
|
|
a)
« 5 »
matchs dans l’année : |
|
|||||||||||||||||||||||||
|
|
|
Dépense
avec l’option A : « 200 € » |
Dépense
avec l’option B : « 400 € » |
300 + 100 |
|
||||||||||||||||||||||
|
|
b)
« 20 »
matchs dans l’année : |
|
|||||||||||||||||||||||||
|
|
|
Dépense
avec l’option A : « 800 € » |
Dépense
avec l’option B : « 700 € » |
300 + 400 |
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
2°)
En désignant par « |
|
|||||||||||||||||||||||||
|
|
a)
la dépense annuelle avec l’option « A » , notée « b)
la dépense annuelle avec l’option « B » , notée « |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
3°)
Faites la représentation graphique des applications affines : « f »
et « g » . Vérifiez
par le calcul les résultats
du tracé ci-contre. ( en abscisse en
€ ; en ordonnée les matchs ) |
|
|
||||||||||||||||||||||||
|
|
4°)
En utilisant le graphique , répondez aux questions
suivantes : Pour
combien de matchs le prix est-il le même pour les deux options ?
……………….. Quelle
est suivant le nombres de matchs annuels , l’option le plus avantageuse ? …………………………………………………………………………………. |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Fiche
4 : Détermination d’une application affine. |
|
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
En
France , les températures s’expriment en degré
Celsius ( noté ° C). Aux
USA , les températures s’expriment en degré
Fahrenheit ( noté ° F). En
désignant par « «
Cette fonction est une application affine , à
« 0°C » correspond « 32
°F » et à « 100°C »
fait correspondre « 212 ° F ». |
|
|||||||||||||||||||||||||
|
|
Puisque « Sachant
que « x = 0 » , « y =
32 » , on peut écrire « Sachant
que « x = 100 » , « y =
212 » , on peut écrire « d’où
terminez le calcul : « l’application
affine cherchée est définie par « |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
· Utilisez ce résultat pour compléter le tableau
ci-dessous. |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
Degré Celsius |
0° C |
100°C |
37°C |
-25°C |
|
|
-40°C |
|
|
||||||||||||||||
|
|
Degré Fahrenheit |
32°F |
212°F |
|
|
0°F |
14°F |
|
|
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
· Faîte la
représentation graphique ( sur une autre feuille )
et contrôlez par simple lecture les résultats que vous venez de trouver. |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
Fiche
5 : Déplacement à vitesse constante. |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
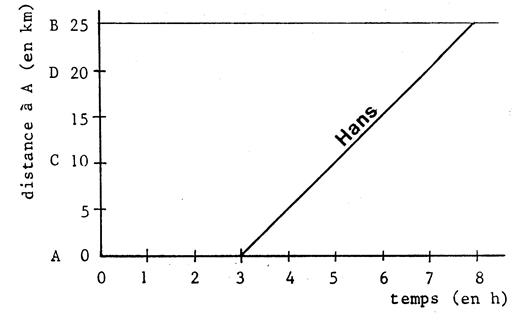
5
marcheurs : Guy , Hans , Jean , Karl et Luc se
déplacent sur un chemin reliant deux villages « A » et
« B » distant de 25 km. Leur
vitesse et constante , elle est la même pour
tous : 5 km /h. Exprimons
en fonction du temps , la distance
« A » de chacun des
marcheurs. Désignons
par « |
|
|||||||||||||||||||||||||
|
|
1°)
Guy part à « Appelons
« A
« A
« On
a alors |
|
|||||||||||||||||||||||||
|
|
2°)
Hans part à « Appelons
« A
« A
« A
« On
a alors C’est
une application affine dont le coefficient
« 5 » est la vitesse du marcheur. |
|
|||||||||||||||||||||||||
|
|
3°)
Jean part à « 0 h » de
« C » situé à « 10 km » de « A » et va en
« B ». Appelons
« j (t) » sa distance à « A ». A
« A
« On
a alors |
|
|||||||||||||||||||||||||
|
|
4°)
Karl part à « Appelons
« A
« A
« On
a alors Vous
constatez que le coefficient
« -5 » de cette fonction est l’opposé de la vitesse du marcheur . Expliquez , verbalement , pourquoi ….. |
|
|||||||||||||||||||||||||
|
|
5°)
Luc part à « Appelons
« A
« A
« Sa
distance à « A » ( en km ) est
alors : « 20 -
……………… » Développez et réduisez
………………………………….. On
a alors : « |
|
|||||||||||||||||||||||||
|
|
Remarque : IL
est possible de démontrer que si un mobile se déplace à « vitesse constante » , la distance parcourue est une application affine du
temps. |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
· Faîtes les
représentations graphiques correspondantes. ( Ce
sont des segments ). On a déjà représenté le déplacement
de « Hans ». Lisez
sur ce graphique « heure »
et « lieu » de rencontre des
marcheurs. Compétez
le tableau. |
|
|||||||||||||||||||||||||
|
|
|
Marcheurs |
Heure |
Distance
de « A » |
|
||||||||||||||||||||||
|
Guy
et Karl |
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||