|
ETUDE du
cours en TRAVAUX AUTO - FORMATIF |
N°9 / 25 |
|
||
|
CONSIGNE : vous devez
répondre aux questions en vous aidant du cours . |
||||
|
N°9 |
LA PROPORTIONNALITE et les calculs sur la
proportionnalité ;son
l’application linéaire . Etude du cours Etude chapitre par
chapitre (des questions peuvent être rajoutées): |
|||
|
|
||||
Prendre une feuille ,
répondre aux questions en vous aidant du cours.
|
VOCABULAIRE
déjà utilisé : (Rappels) |
1a ) Qu’appelle t - on : Rapport ?:
1b) Quel est le modèle mathématique d’un
« rapport » ?
1c)
Compléter le tableau :
|
Exemples : |
Quotient : |
Commentaire : |
|
6 / 2 = 3 |
? |
Le quotient est un
nombre ? |
|
4,5 :2 = |
? |
Le quotient est un
nombre ? |
|
8 : 3 |
? |
Le quotient est une
fraction irréductible dit
« …….. ? ……..» |
2a) ) qu’appelle -t - on « Rapports
égaux » ? :
2b) quel est le modèle mathématique de deux rapports
égaux est l’égalité de deux fractions ?.
2c) Quel
peut être la nature du quotient ?
3 a) Qu’appelle -t - on par « Suite de rapports
égaux » ?
3b
) Quel est son modèle mathématique ?
Traduction en langage mathématique :
3 c) Appliquer : ![]() sont t-ils des
rapports égaux ?
sont t-ils des
rapports égaux ?
FIN du rappel.
|
La
proportionnalité : |
|
Info plus !! et :i |
1°) Donner la définition de la
proportion ??? :
2°) Soit deux cas : On donne deux fractions . Montrer si il y a , ou pas , une proportion
|
Cas : ………………………………… |
|
Cas il n’y a pas …………………. |
|
Soit les deux fractions : Est ce que ces deux fractions forment une proportion ? |
Soit les deux fractions : Est ce que ces deux fractions forment une proportion ? |
|
|
Condition posée ; |
Condition posée : |
|
|
Réflexion : . |
Réflexion |
|
|
Calculs : |
Calculs : . |
|
|
Conclusion : . |
Conclusion : |
3°)
Compléter la phrase :
Lorsque le quotient « semble identique) est identique et que le calcul ne « tombe pas juste (c’est à
dire que reste différent de zéro
) » Une autre possibilité de calcul permet de vérifier si deux fractions
sont égales : il faut calculer le « ………………………………. » . (
on verra cette pratique plus loin dans le cours ) .
4°)
Application : calculer le produit
en croix des deux fractions 8 / 3
et 16 / 6
![]()
5°) Soit la proportion : ![]() ; nommer les
« moyens et les extrêmes »
; nommer les
« moyens et les extrêmes »
6°)
compléter la phrase suivante :
Dans une
proportion le produit des …………………………………………………….
Rappel C d :
les fractions équivalentes :
6°)
Application : : ![]() est - elle égale à
est - elle égale à ![]() ? donner une conclusion .
? donner une conclusion .
Solution :
Calcul n°1: ;
calcul n°2 :
Conclusion :
7°) Qu’est qu’un coefficient de proportionnalité ?
8a °) Quel
peut être la nature de ce nombre ( à
quel ensemble appartient -il ?) :
9°) comment obtient - on un coefficient de proportionnalité ..
9) On
obtient ce coefficient lorsque l’on
divise chaque valeur …………………………………………………….. ( valeur
correspondante : qui occupe le même rang )
…………………………….. .
10) Exemple
Si
deux suites de nombres forment
une suite de nombres proportionnels : si l’on met ces nombres dans un
tableau , on obtient un tableau :……………………………….
Le
tableau ci dessous est appelé « tableau de
proportionnalité »
|
? |
¯ |
1,5 |
4,3 |
9,6 |
Dans cette Ligne supérieure les nombres forment
la « ………………………………. » |
? |
|
3 |
8,6 |
19,2 |
Dans cette Ligne inférieure les nombres
forment la
« ………………………………… » |
11 )
Quelle est la valeur du coefficient de
proportionnalité : ……………………………….
12°) Etablir la suite de nombres
proportionnels et Vérifier par le
produit en croix :
13°) Lorsque
l’on a deux suites de nombres , donner la règle qui permet de calculer le
coefficient de proportionnalité !
|
.i9 |
III )
Rechercher si deux suites de
nombres forment une suite de nombres proportionnels |
14°) Quelle condition faut -il remplir
pour que deux suites de nombres forment une suite de nombres
proportionnels. ?
15°) Soit la première suite S1 = {
2 ; 6 ; 10 } ; soit la
deuxième suite S 2 = {
4 ; 12 ; 20 } , sont - elles
proportionnelles ?
Vocabulaire :
compléter la phrase :
16°) on dit
aussi q ‘ une « équation » est une
« …………………( ?) ………… »
17 °) .iLa fonction linéaire est le modèle algébrique permettant de traiter …………………………………………………………………..( ?)………………
18°) Problème « exemple » : 2 kg de
pommes valent 1, 6 € ; 3 kg valent 2,4 € ; 5 kg valent 4 € .
18a ) comment montrer qu’il y a
« proportionnalité » ? .
On montre qu ‘il y a
proportionnalité en effectuant ( ?) ………………
|
|
= ( ?) |
18b ) compléter la phrase : On peut dire que
le prix à payer est égal
……….( ?) multiplié par
………………..( ?) .
18c)Que désigne la lettre
« y » ? :
18d) Que désigne la
lettre « x » ?
18e) On remplacera la formule de la forme y = a x
par l’équation L?)
18 f) Si le kilogramme de
pomme passe à 1,2 € le kilo ; donner
la formule : ( ?)
19 ) Donner le forme de
la formule ( forme algébrique) (
?) ……………………. ;
20) Compléter la
phrase : la droite d’équation
« y = 1,2x » peut être tracée dans
( ?) …………………………………………………
21)
« vocabulaire » :
traduire l’écriture : f (x) :
( ?) lire « …………………… »
22 ) Compléter la phrase : o n dit que
« y » est obtenu en ( ?)
……..
23 ) Compléter la phrase : On remplacera l’équation « y = 1,2 x » et l’on écrira que la fonction s’écrira : ( ?)
«………………………… »
+Généralisation : On
peut mettre les suites de nombres précédents sous la forme d’
![]()
![]() une suite de rapports égaux
une suite de rapports égaux ![]() =
=![]() =
=![]() =......... ;
=......... ;

On peut dire que cette
suite est égale au rapport des ![]()

Ce rapport est un
coefficient qui est égal au nombre que
l’on nommera « a » .
On peut donc écrire que : ![]() =
=![]() =
=![]() =
= ![]()
On a décidé
de transformer ces rapports de la
forme ![]() par
l’écriture y = ax
par
l’écriture y = ax
c’est une autre forme
d’écriture dite « algébrique », cette écriture algébrique
est une égalité appelée « équation »
.
25 ) Cette
équation « y = a
x » est appelée : « …………………………………… »
.
+Application à des cas concrets
(Adapté à la vie quotidienne)
D’autres applications seront traitées dans le
cours 10 /25 .
Série 1 :
26 ) ►Problème 1
Le prix d’un kg de fruit est de 0,8 €.
Donner une formule permettant de calculer le prix à payer en fonction de la
masse achetée.
Solution
Pour tout achat de ces
fruits , on a : prix à payer = prix
au kg ![]() nombre
de kg
nombre
de kg
22a) Si on appelle
« x » le nombre de kg achetés
et « y » le prix à payer
on écrira l’équation ? :
27) ►Problème 2°)
J’achète des pommes à 1,53 € le kilogramme ;
quelle sera la relation mathématique à
utiliser ?
Solution :
27a) si « y »
est le prix à payer et « x » le nombre de kg ,quel sera est le
coefficient de proportionnalité ?.
27b) Donner la forme de
l’équation de ce que je dois payer :
Applications :
27c) -si je prend 4,5 kg
; je payerai y =
27d ) -si je prend 1, 350 kg ; je payerai y =
2 7 e )
Conclusion : Avec la relation y = 1,53 x
je peux calculer la somme à payer
quelque soit ……………………..; je multiplie la valeur de cette masse par ……………….. .
28 °) ►Problème n° 3
J’ai payé 7,2 €
pour des pommes vendues 0,8 € au kg . Quelle est la masse de pommes
achetées ?
28a) On sait
que la relation à utiliser est
………………….
28b) On connaît « y
= 7,2 » , on peut écrire 7,2 =
…………. ? x
|
Pour calculer
« x » on transforme l’équation : |
|
On simplifie pour obtenir : ![]()
28c) Donc x =
(opération) …………………. ; soit
x = ………….
28 d) conclusion : la masse de pommes achetées est de ………………..
Série 2 :
Autre méthode de résolution d’un problème sur les
proportionnalités :
on raisonne en passant
par le tableau de proportionnalité.
29 ) Problème n° 4 : J’ai payé 7,2 € pour 10 kg pommes combien paierai-je pour 4
kg ?
(on a
établi le tableau suivant)
|
Nombre de kg |
10 |
4 |
|
Prix payé |
7,2 |
( x ) |
Calcul :…………….. x
= ?
Conclusion : le prix
à payer pour 4 kg est de …………………………
+Première approche : nous avons vu précédemment que nous pouvions mettre dans un tableau des valeurs calculées.
30°) Problème
n° 5 : J’ai payé pour des
pommes vendues 2 € au kg . Combien paierai-je si j’achète une masse de 1,5 kg ; 4,3 kg et 9,600 kg ;
pommes achetées ?
30a) Construire le tableau de proportionnalité
|
´ 2 |
¯ |
1,5 |
4,3 |
9,6 |
|
¸2 |
|
3 |
8,6 |
19,2 |
|
+Deuxième
approche : théorique
31°) Problème n°6 :
J’ achète
des pommes vendues 2 € au kg . Combien paierai-je si j’ achète une
masse « quelconque » (
notée par la lettre « x » ) de pommes achetées ?
On demande d ’ établir l’équation et de construire
un tableau ou l’on peut connaître les prix à payer pour
des sacs contenant 1,5 ; 2 ; 2,5 ; 3 ;
4 et 5 ( kilos achetés)
Solution :
31a )On pose :
« x » pour …………………….. ;
« y » pour ……………………… ;
31b) On en déduit
l’équation « y = ? »
 31c)
Construire un tableau de
proportionnalité , précisez !! :
31c)
Construire un tableau de
proportionnalité , précisez !! :
|
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|


31d) construire un tableau . Placer les valeurs
1,5 ; 2 ; 2,5 ; 3 ; 4 et 5 on
sait que : y = 2 x
compléter le tableau.
|
|
x |
1,5 |
2 |
2,5 |
3 |
4 |
5 |
|
|
y |
? |
? |
? |
? |
? |
? |
|
on
Recherche le coefficient de
proportionnalité |
La recherche du
coefficient de proportionnalité est un autre
moyen de traiter les problèmes de proportionnalité.
32
°) Problème n° 7 : j’achète 9 kg de
pommes pour 7,2 € ; une offre
promotionnelle propose un lot de 3 kg de ces mêmes pommes à 2,99 €.
Y a - t-il un rapport de
proportionnalité ? expliquez
comment on doit procéder .
Solution :
32 a) Calculs :
32b) Conclusion :
|
VII. autre activité :
Faire la Représentation graphique d'
une proportion |
33°) compléter la phrase : La représentation graphique d'une situation
de proportionnalité est une …………….. qui passe par l'…………… .( O ) du repère
cartésien.
34°) Exemple
N°8 : Un cycliste se déplace à la vitesse moyenne de 20 km par
heure ( 20 km/h ou 20 km.h-1 ).Déterminer
l’équation « y » distance parcourue(km) en fonction de
« x » durée du parcours(h) ; construire un tableau de proportionnalité avec x = 1 h ; 2h et 3 h ; Tracer
la droite dans un repère cartésien.
34a) Donner l’équation
algébrique : ………………………………
34b)
Compléter : Avec " y " représente : ……………, "x" représente
…………………...

34c) compléter le
tableau :
|
Durée en h. |
1 |
? |
3 |
|
Distance parcourue |
? |
40 |
? |
34 d) Compléter les
colonnes par une lettre majuscule.
Pour la représentation graphique ( on reprend le
tableau précédent on nomme les colonnes )
|
Points ® |
A |
B |
C |
|
Durée en h. |
1 |
2 |
3 |
|
Distance parcourue |
20 |
40 |
60 |
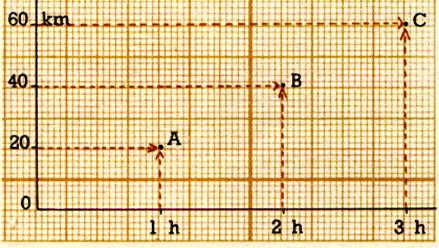
34 e) Tracer le
repère sur « x » 1h = 2
cm ; sur « y » 20 km = 1
cm ) ;
Donner les valeurs des couples de points et puis les
placer dans le repère .
les points
A (….; …..) ; B ( ….. ; …… ) ; C ( ……. ;…….)
|
La représentation graphique est ……………… |
|
|
VIII.
problème résolu ; Activités |
|
35°) Rechercher
un complément d'informations à la lecture de la représentation graphique, et interpréter certains
événements :
|
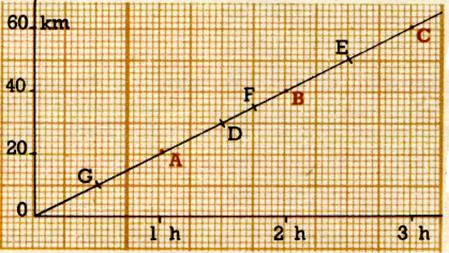
Soit la représentation
graphique ci- contre. « Soit un cycliste
qui quitte un lieu en un point O » . |
|
35a) Compléter le tableau ci - dessous :
|
|
? |
G |
? |
D |
F |
? |
E |
? |
|
Durée en h. |
0 |
|
1 |
|
|
2 |
|
3 |
|
Distance parcourue |
0 |
|
20 |
|
|
40 |
|
60 |
2°) Quel commentaire peut - on faire sur
les points : G :
D ; F et E ?.
35 b ) commentez ce qui se passe au point « G » , au point « D » au point
« F » ; « E »:
|
Pré requis :
repérage et les calculs |
Revoir ce dessus pour ce
qui est du vocabulaire employé. !!!!!!
Dans ce chapitre
A) il faut savoir : compléter
et utiliser un tableau de proportionnalité , et ;
B) il faut savoir déterminer ,
représenter et utiliser l’application linéaire liée à une situation de
proportionnalité .
36°) Application linéaire :
36 a) Que désigne « k » (quelle est
sa nature ?):
36b) L’ ’application
linéaire de coefficient « k » fait correspondre à chaque nombre
« x » le nombre « y »
, traduire en une équation mathématique :
36 c) compléter la phrase : on dira que le produit de « k x » ……………… de « x » par l’application linéaire de coefficient « k » . On dira donc que « …………………..x »
36d) Par quel symbole remplace - t- on l’expression « à pour image » ?
36 e) Traduire en
écriture symbolique : « x à pour image k x » :
36
f ) Compléter la phrase : « y » est ………………………………….
36 g) Si l’application linéaire s’appelle « f » et si « y » est l’image de
« x » ;
traduire en écriture symbolique : y
=……………………..
36 h ) On lira que : chaque valeur
de « y » est obtenu ……………………………….. .
37°) Application linéaire liée à une situation
de proportionnalité .
37 a) on donne : x ![]() -3,5
x est associé à ce tableau de proportionnalité ;
compléter le tableau
-3,5
x est associé à ce tableau de proportionnalité ;
compléter le tableau
|
´ ? ¯ |
x |
- 3 |
- |
0,4 |
1 |
2 |
? |
|
y |
? |
? |
? |
? |
? |
? |
37 b) Représentation graphique . ( voir chapitre ci dessus : 6°
)Représentation graphique d' une
proportion )
Compléter la
phrase : La représentation
graphique de l’application linéaire de coefficient « k » est
……………………………………………………….
37 c) par quels points particuliers passe - t-
elle ?
38°) Coefficient :
soit l’application linéaire f telle que
f ( 2) = (
-13)
38 a) calculer son
« k » :
…………………………..
38 b) généraliser : l’application
linéaire f telle que f(x) = k x
à pour coefficient :?
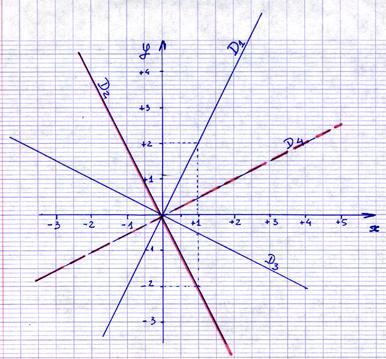
39°) Exemple de représentations graphiques :
que peut -on dire des
droites sur le dessin ? , compléter
les phrases.
|
39 a) La représentation graphique d’une fonction
linéaire est ……………… …………………………… 39 b) D1 ; D2 ; D3 ;
D4 sont des ……………….. ………………………….. 39 c) ces droites sont les représentantes d’une
fonction ………………. 39 d) Quel est le signe de
« k » pour chaque ? |
|
Ceci termine la phase de
découverte du document « cours » , vous devez demander des précisions
si les réponses ne vous ont pas paru « évidente ».