Sur une population définie à l'avance, on rassemble des
informations en effectuant une enquête . On étudie un ou plusieurs caractères (
qualitatif ou quantitatif ) clairement énoncés . Le nombre de réponse attribué
à un caractère est appelé : « effectif »
.On rassemble les résultats en
élaborant une ou des séries statistiques que l'on regroupe dans des tableaux .
Exemple :
On a relevé les performances des 30 élèves d'un même groupe en lancer du
poids.
|
11,4
|
4,10
|
5,70
|
8,4
|
6,00
|
8,60
|
4,7
|
6,75
|
9,70
|
4,9
|
11,1
|
6,60
|
5,4
|
7,40
|
6,95
|
|
9,15
|
5,5
|
9,80
|
5,60
|
7,90
|
5,80
|
8,65
|
8,10
|
6,20
|
10
|
7,30
|
5,85
|
4,40
|
8,05
|
6,30
|
Le statisticien a décidé
après négociation avec le
professeur et pour des facilités l’interprétation des performances , de
regrouper les résultats des élèves en 5
catégories ;Chaque catégorie est
appelée «classe » .
Intervalle et classe : chaque
classe est représentée symboliquement
par l’écriture utilisée pour les intervalles tel que :
|
Borne
mini « A »
|
|
Borne
maxi. « B »
|
|
|
[ …A…. ; …B..[
|
|
|
Valeur
incluse ( signe : [
|
|
Valeur exclue ; signe : [
|
A et B sont des nombres .
Les 5 classes retenues
sont dans l’ordre croissant :
[ 4 ;
5,5 [ ; [ 5,5 ; 7 [ ; [ 7 ; 8,5 [ ; [ 8,5 ; 10 [ ; [ 10 ; 11,5 [
Nous pouvons regrouper les
résultats ( performances des élèves
) dans le tableau ci-dessous:
|
Catégories « classe »
|
Longueur du jet
|
Effectif
|
|
Classe 1
|
[ 4 ; 5,5 [
|
5
|
|
Classe 2
|
[ 5,5 ; 7 [
|
11
|
|
Classe 3
|
[ 7 ; 8,5 [
|
6
|
|
Classe 4
|
[ 8,5 ; 10 [
|
5
|
|
Classe 5
|
[ 10 ; 11,5 [
|
3
|
On demande :
1°) Quel est le caractère observé ? Est - il qualitatif ou quantitatif
? Pourquoi a - t - on
effectué un regroupement en classes ?
2°) Traduire par une phrase la troisième ligne « performance ».
Solution :
1°) Le caractère observé est la longueur du jet .Il est quantitatif
puisqu'il s'exprime par des nombres. On effectue un regroupement en classes
parce que les valeurs sont quelconques .
2°) La longueur du lancer a été comprise entre 7 et 8,5 mètres pour 6 élèves.
Pour facilité l'analyse "rapide" des informations ;on peut
visualiser les résultats obtenus en
construisant, à partir du tableau, un
diagramme .
Les trois principales représentations graphiques couramment utilisées
dans la vie quotidienne sont : le
diagramme à bâtons, le diagramme circulaire et la représentation graphique
appelée "histogramme" .
Recommandation concernant la réalisation d'un
graphique
a)
Choisir l'intervalle- unité qui
permette de représenter correctement le phénomène et qui assure la meilleure utilisation de l'espace disponible.
b)
Indiquer de façon apparente le titre
et la signification des axes .
En conclusion , il ne faut jamais
oublier qu'un graphique , pour être utile , doit se suffire à lui- même et
dispenser le lecteur de toute référence
à un autre document .
|
Lorsque les valeurs prises par un caractère statistique sont distinctes, on construit un diagramme
"bâtons".
En abscisse on trouve les valeurs du caractère, en ordonnée les
effectifs.
|
Info plus !!!! sur le diagramme
"bâtons"
|
|

|
|
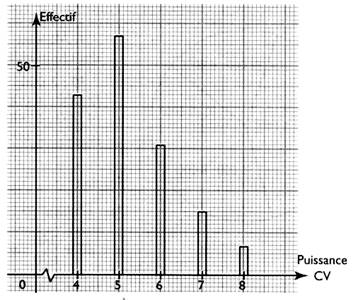
La répartition de la puissance fiscale d'un parc de véhicules est
donnée par le tableau . Construire le diagramme à bâtons correspondant ( en ordonnée
, prendre un mm pour 1 véhicule)
|
|
|
|
|
Puissance fiscale
( c v)
|
Effectif
|
Hauteurs des
bâtons
|
|
4
5
6
7
8
|
43
59
30
13
5
|
43 mm
59 mm
30 mm
13 mm
5 mm
|
|
Lorsque les valeurs prises par un caractère statistique sont
regroupées en classes , on les représente par un histogramme.
|

|
Exemple : On a relevé les
moyennes des notes des 30 élèves d'une classe d'un établissement scolaire. Les
résultats sont regroupés dans le tableau ci-dessous:
On demande :
1°) quel est le caractère observé ? Est - il qualitatif ou quantitatif
? Pourquoi a - t - on effectué un regroupement en classes ?
2°) Quelle est la moyenne la plus
petite et la plus grande obtenue.
|
Moyenne
|
Effectif
|
|
[ 7 ; 9 [
|
7
|
|
[ 9 ; 11 [
|
9
|
|
[ 11; 13 [
|
3
|
|
[ 13 ; 15 [
|
6
|
|
[ 15 ; 17[
|
5
|
Solution :
1°) Le
caractère observé est la note moyenne .Elle est quantitative puisqu'il
s'exprime par des nombres. On effectue un regroupement en classes parce que les
valeurs sont quelconques .
2°) la
moyenne la plus petite obtenue est "7" et la plus grande est
"17"
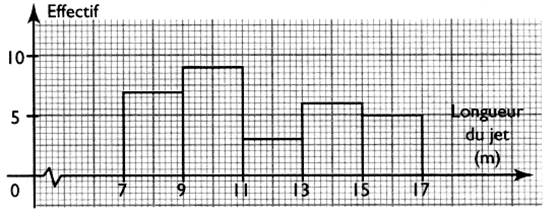
Traduction par un histogramme
cette série statistique :
Pour ce faire on prend 1 cm pour un écart de 2 points en abscisse et 2 mm pour une unité (
effectif) en ordonnée .
|
Note
|
Effectif .
|
Hauteur des
rectangles
|
|
[ 7 ; 9 [
|
7
|
14 mm
|
|
[ 9 ; 11 [
|
9
|
18 mm
|
|
[ 11; 13 [
|
3
|
6 mm
|
|
[ 13 ; 15 [
|
6
|
12 mm
|
|
[ 15 ; 17[
|
5
|
10 mm
|
|
|
|
|
|
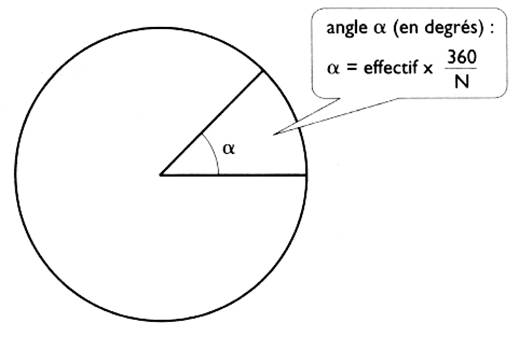
Les mesures des angles
au centre sont proportionnelles aux
« effectifs » correspondants.
Un angle de 360° correspond à l'effectif total "N" .
A un effectif partiel "n" correspond un angle de a = 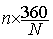
|
|
|
Activité
: on veut construire un diagramme
circulaire ; il faut déterminer les valeurs angulaires (en degré) pour chaque partie composant le
budget .
|
Exemple :
Le budget de la France en 1969 correspond à 171,5
milliards de francs.
Il est réparti ainsi :
45,9 pour
l’ action économique
34 pour l’ éducation
29,4 pour la défense
25,2 pour
l ‘ action sociale
17 pour l’administration générale
6,8 pour l’ habitation
13,1 pour le « divers »
|
On recherche les valeurs angulaires des secteurs
circulaires pour chaque domaine :
"45,9"
pour l’ action économique sera
représentée par un secteur angulaire d' angle : a = 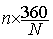 =
= 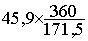 = 96,4 °
= 96,4 °
"34" pour l’ éducation sera représentée
par un secteur angulaire d' angle : a = : 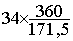 » 71,37 °
» 71,37 °
"29,4" pour la défense sera représentée
par un secteur angulaire d' angle : a = : 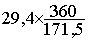 » 61,71°
» 61,71°
"25,2" pour l ‘ action sociale sera représentée par
un secteur angulaire d' angle : a =:  » 52,90°
» 52,90°
"17" pour l’administration générale sera
représentée par un secteur angulaire d' angle : a =: 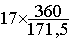 »
35,69°
»
35,69°
"6,8" pour l’ habitation sera représentée
par un secteur angulaire d' angle : a =:  » 14,27°
» 14,27°
"13,1" pour le « divers » sera
représentée par un secteur angulaire d' angle : a =: 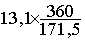 » 27,50 °
» 27,50 °
|
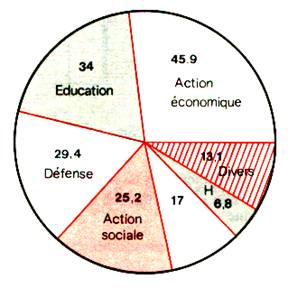
La représentation graphique est le disque
ci-contre :
Faire la somme des valeurs angulaires calculées.
|
Mesurer chaque valeur angulaire , et faire la
somme . comparer avec les calculs .
|
Autre exemple :
Une enquête sur le montant des commandes dans un entreprise a donné les
résultats suivants :
|
1 )Montant des
commandes
|
2) nombre de
commandes
|
|
[0; 2000 [
[2 000; 4 000 [
[4 000; 6 000 [
[6 000; 8 000 [
|
60
120
240
180
|
On demande de compléter de trouver les valeurs angulaires des secteurs
et de construire le diagramme circulaire .
Solution : On calcul "N" =
60+120+240+180 = 600.
Et on utilise la formule suivante : a = 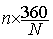
|
Calcul pour chaque
classe :
|
Représentation
graphique :
|
|
[0; 2000 [ :
a = 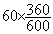 = 36° = 36°
[2 000; 4 000 [ :
a = 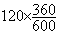 = 72° = 72°
[4 000; 6 000 [ :
a
= 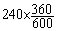 = 144° = 144°
[6 000; 8 000 [ :
a
= 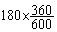 =
108° =
108°
Remarque : Faire la somme des valeurs
angulaires pour vérifier si elle est
égale à 360°
|
Activités :Mesurer avec un rapporteur la valeur angulaire de chaque angle au centre .

|
|
Leçon
|
Titre
|
|
N°12
|
TRAVAUX
d ’ AUTO - FORMATION sur
LES REPRESENTATIONS DE
SERIES STATISTIQUES.
|
TRAVAUX N° 12
d ’ AUTO - FORMATION : CONTROLE
1°)Statistique descriptive . Compléter les
phrases suivantes avec les mots suivants :
cherche à savoir ; représentations ;
grandeurs ; le saisie ; regroupement : enquête ; le
dépouillement ;
Elle commence là où la
donnée d'un tableau de nombres exprime des …………….. liées au phénomène étudié .
Pour faire une analyse statistique il faut déterminer ce que l'on
………………………… et organiser une ……………… ( questionnaire et entretiens ).
L'enquête réalisée commence
alors le ……………….. et le ………… des informations collectées vient ensuite le
…………………… des données et leur …………………………...
Compléter les phrases suivantes :
population ; séries ;enquête ; effectif ; tableaux ;
caractères .
Sur une ………………….définie à l'avance , on rassemble
des informations en effectuant une
…………………. .
On étudie un ou plusieurs ……………………
( qualitatif ou quantitatif ) clairement énoncés . le nombre de réponse
attribué à un caractère est appelé : …………………. .
On rassemble les résultats en élaborant une ou des …………
statistiques que l'on regroupe dans
des …………. ; .
|
2°) Représentation d'une série statistique par un diagramme.
|
Pour facilité l'analyse
"rapide" des informations ;que peut-on construire pour visualiser les
résultats d’une enquête ?
Nommer
les trois principales représentations graphiques couramment utilisées
dans la vie quotidienne sont :
……………………………………….
A)
Représentation d'une série statistique
par un diagramme à bâtons.
Quand construit - on un diagramme
en bâtons ?
Que trouve - t- on en abscisse ?
Que trouve - ton en ordonnée ?
Quel nom donne - t - on au
diagramme ci dessous ?
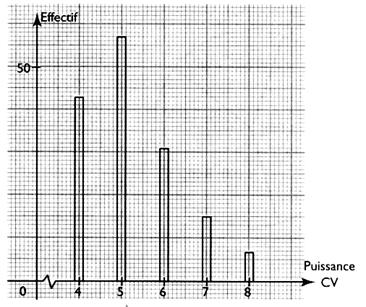
|
B) Représentation d'une série
statistique par un "histogramme"
|
1°) quel nom donne - t - on à la représentation graphique des valeurs prises par un caractère
statistique regroupées en classes ?
2°) Dans un histogramme qu’est ce
qui doit - être proportionnel au
effectifs ?
|
C) Représentation d'une série statistique par un diagramme à secteurs circulaires.
|
1°) Dans un diagramme à secteurs circulaires qu’est ce qu’est
proportionnel aux effectifs ? .
2°) à quelle valeur angulaire
correspond l ’ effectif
total « N »?
3°) A quel calcul l’angle « alpha » correspondra un
effectif partiel « n » ?
4°) soit la formule : a
= 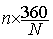 ; à quoi sert- elle ?
; à quoi sert- elle ?
Que désigne "n" : ?
Que désigne "N" ?
Que représente "a" ?
EVALUATION 1 :
On a relevé les performances des 30 élèves d'une classe en lancer du
poids.
|
11,4
|
4,10
|
5,70
|
8,4
|
6,00
|
8,60
|
4,7
|
6,75
|
9,70
|
4,9
|
11,1
|
6,60
|
5,4
|
7,40
|
6,95
|
|
9,15
|
5,5
|
9,80
|
5,60
|
7,90
|
5,80
|
8,65
|
8,10
|
6,20
|
10
|
7,30
|
5,85
|
4,40
|
8,05
|
6,30
|
Les résultats sont regroupés dans le tableau
ci-dessous:
|
Longueur du jet
|
Effectif
|
|
[ 4 ; 5,5 [
|
5
|
|
[ 5,5 ; 7 [
|
11
|
|
[ 7 ; 8,5 [
|
6
|
|
[ 8,5 ; 10 [
|
5
|
|
[ 10 ; 11,5 [
|
3
|
On demande :
1°) quel est le caractère observé ? Est - il qualitatif ou quantitatif
? Pourquoi a - t - on effectué un regroupement en classes ?
2°) Traduire par une phrase la troisième ligne .
EVALUATION n°2 .
Exercice : 4 familles n'ont pas d'enfants . Compléter le
diagramme avec les données suivantes :
|
Nombre de familles
|
4
|
2
|
0
|
5
|
6
|
2
|
|
Nombre d’enfants .
|
0
|
1
|
2
|
3
|
4
|
5
|

EVALUATION n°3 La répartition de la
puissance fiscale d'un parc de véhicules est donnée par le diagramme en
bâtons . ( en ordonnée ,on a prit un mm
pour 1 véhicule) . Compléter le tableau : donner les effectifs par
puissances fiscales.
|
Puissance fiscale
( c v)
|
Effectif
|
Mesurer les Hauteurs des bâtons
|
|
4
5
6
7
8
|
|
|

Evaluation 4 : On donne le
tableau suivant construire le diagramme
« bâton ».
Enoncé : La répartition de la puissance
fiscale d'un parc de véhicules est donnée par le tableau .
|
Puissance fiscale
( c v)
|
Effectif
|
Mesure des Hauteurs des bâtons
|
|
4
5
6
7
8
|
43
59
30
13
5
|
|
Construire le diagramme à bâtons correspondant .( en ordonnée , prendre un mm pour 1 véhicule)
|
B) Représentation d'une série
statistique par un "histogramme"
|
EVALUATION 5: On a relevé les moyennes des notes des 30 élèves
d'une classe d'un établissement scolaire. Les résultats sont regroupés dans le
tableau ci-dessous:
|
Moyenne
|
Effectif
|
|
[ 7 ; 9 [
|
7
|
|
[ 9 ; 11 [
|
9
|
|
[ 11; 13 [
|
3
|
|
[ 13 ; 15 [
|
6
|
|
[ 15 ; 17[
|
5
|
On demande :
1°) quel est le caractère observé ? Est - il qualitatif ou quantitatif
? Pourquoi a - t - on effectué un regroupement en classes ?
2°) Quelle est la moyenne la plus
petite et la plus grande obtenue.
3°) Construire l’histogramme de cette série statistique :
Pour ce faire on
prend 1 cm pour un écart de 2 points en
abscisse et 2 mm pour une unité ( effectif) en ordonnée .
|
Note
|
Effectif .
|
Calculs des
hauteur des rectangles
|
|
[ 7 ; 9 [
|
7
|
|
|
[ 9 ; 11 [
|
9
|
|
|
[ 11; 13 [
|
3
|
|
|
[ 13 ; 15 [
|
6
|
|
|
[ 15 ; 17[
|
5
|
|
|
C) Représentation d'une série statistique par un diagramme à secteurs circulaires.
|
EVALUATION 6 :
énoncé : Le budget de la France en 1969 correspond à 171,5
milliards d’ euros.
Il est réparti ainsi :
45,9 pour l’
action économique
34 pour l’ éducation
29,4 pour la défense
25,2 pour
l ‘ action sociale
17 pour l’administration générale
6,8 pour l’ habitation
13,1 pour le « divers »
on veut construire un diagramme circulaire ; il
faut déterminer les valeurs angulaires
(en degré) pour chaque partie composant le budget .
Question : Construire un diagramme circulaire .
EVALUATION 7 :
Enoncé : Une enquête
sur le montant des commandes dans un entreprise a donné les résultats suivants
:
|
1 )Montant des commandes
|
2) nombre de commandes
|
|
[0; 2000 [
[2 000; 4 000 [
[4 000; 6 000 [
[6 000; 8 000 [
|
60
120
240
180
|
Questions :
1°) calculer la valeur de l’effectif total ( N ).
2°) Trouver , par le calcul des
valeurs angulaires des secteurs .
2°) Construire le diagramme circulaire .
Série 2 Suite de l ’
EVALUATION:
A) Diagramme circulaire .
On pose à 50 lycéens et lycéennes la question :
"combien de fois es - tu allé au cinéma au cours des deux derniers mois ?"
On obtient les réponses suivantes :
2-5-4-1-6-3-2-2-5-4- 1-4-3-2-1-5-2-1-5-3- 1-5-4-6-1-1-4-5-2-1- 4-3-5-6-3-1-2-5-4-5- 6-2-4-2-5-1-2-4-3-3.
a)
Quel est le caractère
observé ?
b)
Est -il quantitatif ou
qualitatif ?
c)
Compléter le tableau
suivant :
|
Nombre
de séances
|
Effectifs
|
|
1
|
|
|
2
|
|
|
3
|
|
|
4
|
|
|
5
|
|
|
6
|
|
|
Total
:
|
|
d)
construire un diagramme
circulaire ( diamètre 8cm)
B)
Diagramme à bâtons :
On recense le nombre d'enfants dans les 30
familles d'un lotissement : on obtient
les résultats suivants : 0 enfant dans 4
familles ; 1 dans 5 familles ; 2 dans 11 familles ; 3 dans 6 familles; 4 dans 3
familles et 5 dans une famille.
Regrouper ces résultats dans un tableau et
construire le diagramme à bâtons .
C) Diagramme circulaire :
exploiter les données du tableau suivant :
Lecture d’un tableau :
|
|
Garçons
|
Filles
|
Total
|
|
Cinéma
|
8
|
|
12
|
|
Sport
|
|
|
|
|
Lecture
|
6
|
1
|
|
|
TOTAL
|
|
10
|
28
|
Questions :
1)
quel est le nombre d’élèves
de cette classe ?
2)
Combien y a t- il de
garçons dans la classe ? ; de filles ?
3)
Que représente le nombre
« 12 » du tableau ? et le
nombre « 8 » ?
4)
Compléter ce tableau .
|
|
Garçons
|
Filles
|
Total
|
|
Cinéma
|
8
|
|
12
|
|
Sport
|
|
|
|
|
Lecture
|
6
|
1
|
|
|
TOTAL
|
|
10
|
28
|
5)
Combien d’élèves ont pour
loisir favori le cinéma ?
6)
Parmi les garçons combien
ont pour loisir favori le cinéma ?
Construire un diagramme circulaire spécifique aux garçons et aux filles. Le
diamètre du disque sera de 8 cm .
D) HISTOGRAMME:
Au cours d'un examen , les 40 candidats ont obtenu
les résultats suivants :
15 - 1 - 6 -13 -15 - 1 8 - 10 - 18 - 11 -14 -14 - 5
- 6 - 9 - 15- 12 - 17 - 7- 2 - 17- 1 - 9 - 8 -18 - 5 - 15 - 13 - 6 - 8 - 10 -
16 - 11 - 9 - 11 - 13 - 12 - 6 - 14 -
10 ;19 .
1°) Répartir ces résultats dans des classes
d'amplitude "5" :
2°) dresser un tableau. (comme ci dessous )
|
Classe :
|
Effectif
|
|
[0; 5 [
|
|
|
……..
|
|
|
Total
:
|
|
3°) construire un histogramme .
E) Diagramme
« bâtons ».
A partir du
diagramme bâtons compléter le tableau
suivant:
|
Diagramme
à bâtons
|
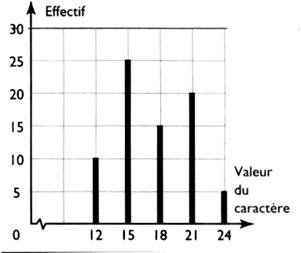
|
|
Valeur
du caractère
|
Effectif
|
|
12
|
|
|
15
|
|
|
18
|
|
|
21
|
|
|
24
|
|
|
Total
:
|
|
F ) Diagramme à secteurs circulaires .
La consommation moyenne d'eau en France se répartit
suivant le tableau .
Pour cent litres (100 l ) :
|
Industrie
|
20
l
|
|
Agriculture
|
70
l
|
|
Usage domestique.
|
10
l
|
On veut construire le diagramme à secteurs
circulaires qui traduit cette situation.
1°) sachant que les angles au centre des secteurs
circulaires sont proportionnels aux consommations correspondantes, calculer les
angles des trois secteurs.
2°) Dans un disque de rayon 5 cm, construire le diagramme à
secteurs.
G) Diagramme circulaire .
Le budget
de la France en 1969 correspond à 171,5 milliards d’ euros.
Il est réparti ainsi :
45,9 pour l’action économique.
34 pour l’éducation
29,4 pour la défense.
25,2 pour l ‘ action sociale.
17 pour l’administration générale.
6,8 pour l’habitation.
13,1 pour le
« divers ».
On veut construire le diagramme à secteurs
circulaires qui traduit cette situation.
1°) sachant que les angles au centre des secteurs
circulaires sont proportionnels aux consommations correspondantes , calculer
les angles des trois secteurs .
2°) Dans un disque de rayon 4 cm ,
construire le diagramme à secteurs.










