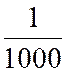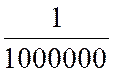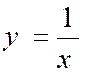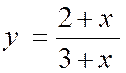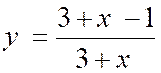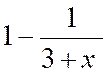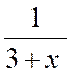Accroissement :

Définition :

Soit  une quantité variable . Celle-ci   passe donc d’une valeur « a » , appelée « valeur initiale »  , à une seconde valeur « b » , appelée « valeur finale » . En calculant la quantité  «  b – a » , on obtient une valeur appelée « accroissement » , ( on dit aussi :  excès de  b-a   de la valeur finale sur la valeur initiale .

Ainsi , si une variable « x » prend successivement les deux valeurs «  x = 1 ; x = 3 » , la valeur initiale est « 1 » et la valeur finale est « 3 » , l’accroissement est « 3-1= 2 »    

L’accroissement est positif , négatif ou nul, suivant que la valeur finale est supérieure , inférieure ou égale à la valeur initiale .

De la définition précédente il résulte que :

La valeur  finale est  égale à la  valeur initiale augmentée de l’accroissement .

Si l’on désigne par « h » l’accroissement de «  b – a » ,on a :   «  b – a = h » ou   « b = a + h »

Le est « 3 »

Notation :

Pour désigner l’accroissement d’une quantité, on fait généralement précéder la lettre qui désigne cette quantité de la lettre grecque :     ( delta)

Ainsi « x »    désigne «  l’accroissement de  x » ;  « y »    désigne «  l’accroissement de y » 

Remarque :  Il faut bien faire attention que le symbole  « x » désigne un seul nombre, que ce n’est pas le produit de  «  par x »  . Les deux lettres «  »et  « x » font corps et leur  ensemble joue le rôle d’une seule lettre.        

lm

Accroissement d’une fonction :

Considérons une fonction « y » d’une variable «x »

Supposons que : 

Pour  « x » = a          ,  on   ait     y = A

Et que

Pour  « x » = b            , on ait   y = B        

En passant de la valeur initiale « a » à la valeur finale « b » , « x »  a subi  un accroissement    « x = b – a »   

De son côté, la fonction « y » a passé de la valeur « A » à la valeur « B » , et a subi un accroissement : « y = B – A »

L’accroissement  «  B – A » est ce qu’on appelle « l’accroissement »de la fonction correspondant à l’accroissement «  b – a » de la variable.   

Soit , par exemple , la fonction  y = 2 x – 3

Pour « x » = 1    on a : y = -1

Pour  « x » = 4    on a :  y = 5

La variable  « x »  a subi l’accroissement   : « x = 4  – 1 = 3  » 

La fonction a subi l’accroissement correspondant :   « y = 5  – (-1) =  6 »

Soit encore la fonction : x² + x + 1 

Pour « x » = -2      on a : y = 3

Pour  « x » = - 1    on a :  y = 1 

La variable  « x »  a subi l’accroissement   : « x = - 1   –  ( - 2)  = + 1   » 

La fonction a subi l’accroissement correspondant :   « y = 1   – 3  =  - 2  »   

Limites :

Chacun de nous a la notion vulgaire de « la limite » d’une quantité variable.

Si l’on veut préciser un peu , au point de vue mathématique , cette notion, on peut dire : qu’une quantité variable « y » a pour « limite » un nombre « b », ou encore « tend vers b » , si elle peut devenir aussi voisine qu’on le voudra du nombre « b » si la différence  «  y – b » peut devenir, en valeur absolue, aussi petite qu’on le voudra.

Par exemple : si l’on considère la fonction :  y =  – 2 x  + 3

Cette fonction « y » a pour « limite 3 » , lorsque  « x » tend vers zéro.

La différence «  y – 3 » est, en effet, en valeur absolue égale à la valeur absolue de « 2x » ; elle peut donc devenir aussi petite qu’on voudra pour des valeurs aussi petites de « x » . Ainsi elle sera plus petite que  si « x » est plus petit que   ( en valeur absolue), elle sera plus petite que   si « x » est plus petit que , etc. 

Info ++

Voici encore d’autres exemples , déjà rencontrés :

Une fraction dont le dénominateur croît indéfiniment tend vers zéro. Ainsi la fraction :  tend vers zéro quand « x » croît indéfiniment , car :

Pour «  x = 100 »    ;       y = 0,01 

Pour «  x = 1 000 »    ;       y = 0,001 

Pour «  x = 1 000 000 »    ;       y = 0,000 001 

Et ainsi de suite……

On peut prendre la valeur de « x » assez grande que « y » soit aussi voisin de zéro qu’on le voudra.

En arithmétique , on apprend que quand on ajoute un même nombre aux deux termes d’une fraction , cette fraction se rapproche de l’unité.

Quand le nombre que l’on ajoute « croît indéfiniment » , la fraction tend vers « 1 » .

Ainsi considérons la fraction  , ajoutons un même nombre positif « x » aux deux termes ; la nouvelle fraction     croît avec « x »  et tend vers « 1 » quand « x » croît indéfiniment.

Il suffit, pour le voir, d’opérer comme nous l’avons fait au paragraphe précède.

On écrit   = 

Quand « x » croît ;   décroît  , donc la partie soustractive de « y » diminue et « y » croît .

Quand « x » croît indéfiniment     tend vers zéro, donc « y » tend vers  « 1 » , puisque la différence « 1-y »  égale  à    devient aussi petite que l’on veut.

Nous admettrons , à ce niveau, sans démonstration que 

Si plusieurs   quantités variables ont des limites , leur somme ou leur produit a une limite qui est la somme ou le produit de ces limites.

Nous admettrons aussi que :

Si deux quantités variables ont des limites : leur quotient a une limite qui est le quotient des limites , pourvu que la limite du dénominateur soit différent soit différente de zéro.

Lorsque le dénominateur d’une fraction tend vers zéro , et que le numérateur  reste différent de zéro , la fraction croît indéfiniment. 

Voir les exemples ……………….

Lecture:    La règle de trois :  limites de son domaine .   Essai pour étendre ces limites :

Des limites :  A propos  des dérivées  nous rencontrerons une notion importante : celle de « limite » qu’il nous faut définir .

Considérons un segment de droite AB représentant l’unité :

Soit M₁ le milieu de AB , AM₁ représentant    le milieu ,soit M₂  le milieu de M₁B , M₁ M₂ représente le quart ( ) , soit M₃ le milieu  de M₂ B , M₂ M₃ représente le   etc ; ….Soit M₄ le milieu de …..

Il est évident que les points « M » successifs se rapprocheront constamment du point « B » mais ne l’atteindront jamais puisque chaque point « M » est le milieu d’un segment de droite ayant justement « B » comme extrémité.

Il en résulte que la somme :

 S  =  ++ + +++ ……

Se rapproche  constamment de l’unité lorsque le nombres de ses termes augmente indéfiniment , elle peut n’en différer que d’une quantité aussi petite que l’on voudra mais elle ne sera jamais rigoureusement égale à l’unité . On dit que « S » a pour limite 1 ou tend vers 1 lorsque le nombre de ses termes augmente indéfiniment .

Dans certains calculs on a à considérer plusieurs quantités u , v , w qui tendent respectivement vers des limites u₁  , v₁ , w₁    . Nous admettrons , sans le démontrer , que la somme  u + v + w  a pour limite u₁  + v₁ + w₁     , que le rapport     a pour limite       , que le produit    u . v . w   a pour limite   u₁ . v₁ . w₁

Exemple   sur la   notion de dérivée :

Considérons la fonction y = x²    ( 1)

                   Si la variable « x » s’accroît d’une quantité très petite appelée (delta de « x » ) et noté : D x  la variable devient x + D x .

                        La fonction « y » s’accroît d’une quantité correspondante D y et devient  y + D y

       Proposons nous de calculer D y  en fonction de D x puis le rapport

Appliquons la formule (1) . Cette formule nous indique que la valeur de la fonction se calcule , en élevant au carré la valeur correspondante de la variable soit :                    y + D y =   ( x + D x)  ²

y + D y =    x² + 2 x .D x  + D x ²         (développement : SOS )

   supprimons y = x²  dans les deux membres

D y =     2 x .D x  + D x ²

le rapport  s’obtient en divisant les deux membres par D x :

soit         =   2 x  + D x

On appelle dérivée de la fonction y = x²  , par rapport à « x » , la valeur limite du rapport  lorsque D x tend vers zéro. Il apparaît immédiatement que si D x s’évanouit   tend vers 2x ;

« 2x » est la dérivée de « y » = x² par rapport à « x »

Définition : la dérivée d’une fonction est la limite , vers laquelle tend le rapport de l’accroissement de la fonction à l’ accroissement correspondant de la variable , lorsque celui-ci « s’évanouit »

Remarque :

Pas de travaux auto formatifs…..