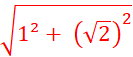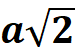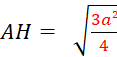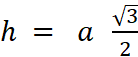|
|
|
|
|
Classe 3ème collège. |
|
|
|
|
|
|
|
|
|
|
|
|
ENVIRONNEMENT du
dossier :
|
2.
4ème collège : le
triangle rectangle et « Pythagore ». 3.
Classe de 4ème :
le théorème de Pythagore. |
1.
Pythagore :application du théorème |
|
|
|
Fiche 3ème : PYTHAGORE dans le plan et dans l’espace. |
|
|
|
Fiche 1 : Le théorème de Pythagore. |
|
|
|
Fiche
2 : Réciproque du théorème de Pythagore. |
|
|
|
Fiche
3 : Longueurs dont la mesure s’exprime avec un radical. |
|
|
|
Fiche
4 : Diagonale d’un rectangle ou d’un carré. |
|
|
|
Fiche
5 : Triangle équilatéral. |
|
|
|
Fiche
6 : Des
démonstrations dans l’espace. |
|
|
|
Fiche
7 : Droite perpendiculaire à un plan . |
|
|
|
Fiche
8 : Calculs
dans le cube. |
|
|
|
Fiche
9 : Situations problèmes. |
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
|
|
|
|
||||||||||
|
|
|
|
||||||||||
|
|
Fiche
1. Le théorème de Pythagore. |
|
||||||||||
|
|
Rappelons ce
théorème étudié en 4ème . |
|
||||||||||
|
|
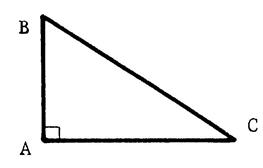
Si « ABC » est un triangle rectangle en
« A » alors : BC² = BA² + AC² |
|
|
|||||||||
|
|
|
|||||||||||
|
|
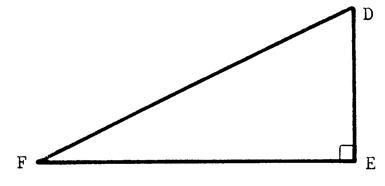
Activité : exercice 1 : FDE est un
triangle rectangle en « E ».
L’unité est le cm. Sachant que « DE = 3 » et
« EF = 6 » , calculez
« DF ». Donnez la valeur exacte de « DF » sous
forme simplifiée puis donnez une valeur approchée de « DF » à 10
-3 près. |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
Activité : exercice 2 : « GKH » est un triangle rectangle en « H ». L’unité est le cm. Sachant que « GK = 41 » et
« HK = 9 » , calculez
« GH ». |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
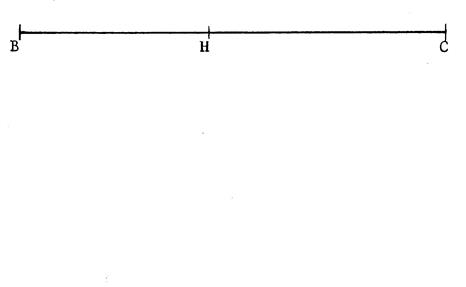
Activité : exercice 3 : Dessinez
un triangle
« ABC » rectangle en
« A » dont on donne l’hypoténuse [BC] et le pied « H » de
la hauteur issue de « A ». · Sachant que « BC = 18 cm »
et « BH = 8 cm », en
appelant « O » le centre du cercle circonscrit au triangle « ABC », calculez ( en
cm) « AO » , « AH » , « AB », « AC ». |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
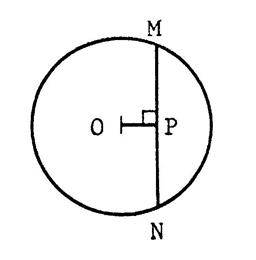
Activité : exercice 4 : On donne un cercle de centre « O » et
de rayon « R= 26 cm ». [MN ] est une corde
telle que « MN= 48 cm ». « P » étant le projeté de
« O » sur (MN) , calculez
« OP ». |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
Fiche 2 : Réciproque du théorème de
Pythagore |
|
||||||||||
|
|
Vous avez vu dans la leçon précédente :le théorème suivante. |
|
||||||||||
|
|
Si dans un triangle, le carré d’un des côtés est
égal à la somme des carrés des deux autres côtés ,
alors ce triangle est rectangle. |
|
||||||||||
|
|
|
|
||||||||||
|
|
Exercice 1 : Dans les quatre cas ci-dessous , dites si les triangles sont rectangle
« oui » ou « non ». |
|
||||||||||
|
|
|
Triangle |
Longueurs
des côtés en cm. |
Triangle
rectangle « oui » ou
« non ». |
|
|
||||||
|
|
« ABC » |
AB =
3,4 ; BC = 3 ; CA = 1,6 |
|
|
||||||||
|
|
« DEF » |
DE =
4 ; EF = 5 ; FD = 6 |
|
|
||||||||
|
|
« GHK » |
GH = |
|
|
||||||||
|
|
« LMN » |
LM = |
|
|
||||||||
|
|
|
|
||||||||||
|
|
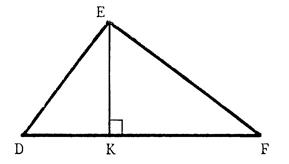
Exercice 2 : ci-contre un triangle
« EDF » . [EK] est hauteur. Sachant que les dimensions sont en cm : EK =
12 ; DK = 9 ;et KF = 16 , faites les
calculs nécessaires pour savoir si le triangle « EDF » est
rectangle ou non. |
|
|
|||||||||
|
|
Exercice 3 : Un triangle
« ABC » dont le côté . [AC] à une
longueur qui peut varier. On sait que ( en cm) AB
= 2 et BC = 1°) Déterminez « AC » de telle sorte
que le triangle « ABC » soit rectangle en « B ». 2°) Même question pour obtenir un triangle
« ABC » rectangle en « A3 puis en « C » . |
|
||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||
|
|
Fiche 3 : Longueurs dont la mesure s’exprime
avec un radical. |
|
|
|||||||||
|
|
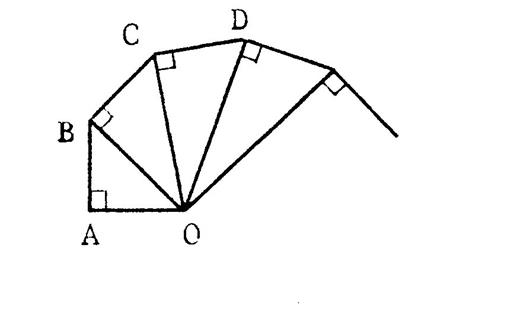
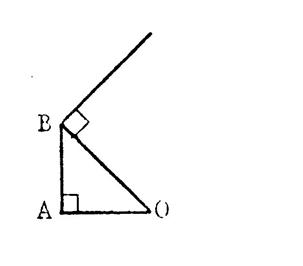
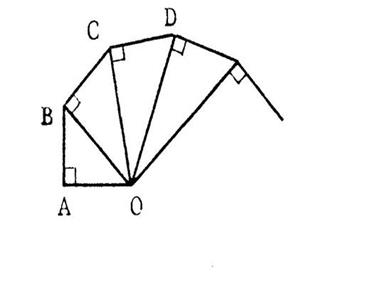
Observez la figure ci-contre. « OA = 1 » (l’unité est le cm) OAB est un triangle rectangle en
« A » tel que « AB =
1 » Calculez « OB » .
Vous trouvez « OB = ……… ( 1² + 1² = 2 ) ; OB = OBC est un triangle rectangle en « B » tel
que « BC = 1 » Calculez
« OC ». Vous trouvez : OC = …… |
|
|
|||||||||
|
|
OCD est un triangle rectangle en « C » tel que CD = 1. Calculez OD . Vous
trouvez OD = ………………………… |
|
||||||||||
|
|
· Poursuivez la construction ( en colimaçon). · Placez les points « E » ,
« F » , « G » , « H » , « I » , « J ». Par le calcul , vous
trouvez : OE = ………………. ; OF
= ……………. ; OG = …………. ; OH = …………….. ; OI = ………………… ; OJ
= ……………. |
|
||||||||||
|
|
|
|
||||||||||
|
|
Exercice : Construisez un segment dont la mesure de la longueur ( en cm ) est (Indication : 13 = 4 + 9 ) |
|
||||||||||
|
|
|
|
||||||||||
|
|
Fiche 4 : Diagonale d’un rectangle ou d’un
carré. |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
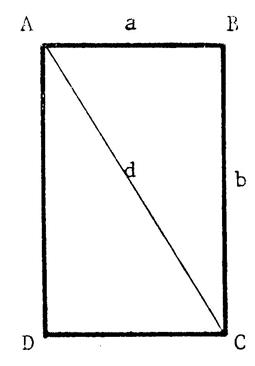
Rectangle : « ABCD » est un rectangle . AB = a ;
BC = b ; AC = BD = d . Calculons “d”: AC² = AB² + ……… C’est à dire : d² = a² + ………
Le rectangle ci-contre est tel que ( en mm) ; a
= 28 ; b = 45 . Mesure AC ( en mm ) . Vous
lisez AC = …………. Par le calcul : AC = |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
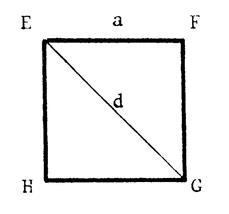
Carré : EFGH est un carré de côté « a » ( « a »
est positif ). Appelons « d » la longueur de chaque
diagonale. Calculons « d » : « d = |
|
|
|||||||||
|
|
|
Théorème : Dans tout
carré de côté « a » et de diagonale « d » : d = |
|
|
||||||||
|
|
Exercice
2 : OAB est un triangle rectangle isocèle ( OA = AB ). Construisez successivement ( en
colimaçon) Les triangles rectangles isocèles OBC , OCD , ODE . Sachant que OA = 5 ,
calculez OB , OC , OD , OE . Sachant que OA = L ,
calculez OB , OC , OD , OE. |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
Fiche 5 : Triangle équilatéral. |
|
||||||||||
|
|
|
|
||||||||||
|
|
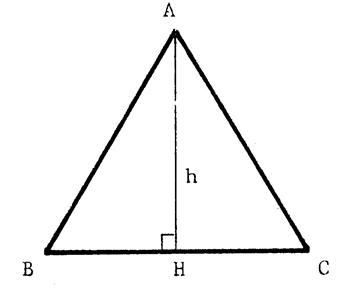
« ABC » est un triangle équilatéral de
côté « a » ( a > 0) . [AH] est
une hauteur . Appelons « h » la longueur
« AH ». Nous allons calculer « h » en fonction
de « a ». Dans le triangle « ABH » rectangle en
« H » , « AB= a » , « BH = Grâce au théorème de Pythagore : AH² = AB² -
BH²
|
|
|
|||||||||
|
|
Donc : |
|
||||||||||
|
|
|
|
||||||||||
|
|
Théorème : Dans un triangle
équilatéral de côté « a » et de hauteur « h » : |
|
||||||||||
|
|
|
|
||||||||||
|
|
Activité : On donne un cercle de centre « O » et
de rayon « R ». [ AB ] est un diamètre. La médiatrice
de [ OB ]
coupe (OB) en « H » et le cercle en « M » et
« N ». 1°) Démontrez que « OMB » est un
triangle équilatéral. 2°) Calculez en fonction de « R » : « MH »
, « MN » , « AM ». 3°) Que pouvez-vous dire du triangle
« AMN » ? ( faîtes une démonstration). |
|
||||||||||
|
|
|
|
||||||||||
|
|
|
|
||||||||||
|
|
Fiche 6 : Des démonstrations dans l’espace. |
|
||||||||||
|
|
|
|
||||||||||
|
|
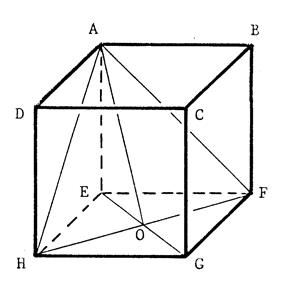
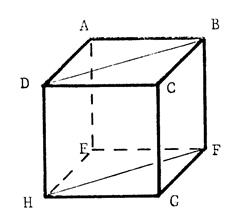
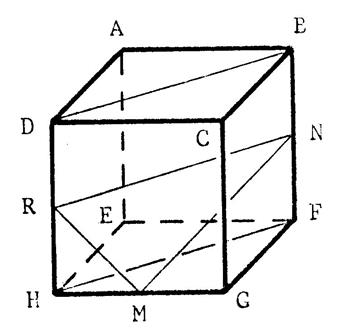
« ABCDEFGH » est un cube, c'est-à-dire un
solide dont les 6 faces sont des carrés. «Appelons « a » la longueur en (cm) des
arêtes. La longueur
(L) (en cm) des diagonales de ces carrés est donc égale à : « L
= Vous en déduisez que le triangle
« AHF » est un triangle équilatèral. |
|
|
|||||||||
|
|
· Les diagonales du carré « EFGH » se coupent en
« O ». Que pouvez-vous dire de [ AO
] pour le triangle
« AHF » ? ……………………………………………………………………….. Quelle est la longueur ( en
cm) de « AO » ? …………………………………………………………… ; |
|
||||||||||
|
|
Nous allons démontrer par le calcul que les
droites ( AE ) et
( EG ) sont perpendiculaires. |
|
||||||||||
|
|
Considérons le triangle « AEO » et
démontrons qu’il est rectangle en « E ». [ EO ] est une
demi-diagonale du carré
« EFGH » donc « EO = ……….. » ;
« EO² = …………. » ; « « EA =
……….. » ; « EA² = …….. » Vous avez trouvé que « AO = « EO² + E A² = |
|
||||||||||
|
|
Si nous faisons le point : [ AE ] ; [ HE ] ; [ EF ] ; sont des
arêtes du cube . Donc (AE) est perpendiculaire à ( EH ) et à ( EF ). ( EH ) et ( EF ) déterminent un plan et on vient de
prouver que ( A E ) est perpendiculaire à ( EG ) qui est une autre droite de
ce plan. · A votre avis , ( AE ) est-elle
perpendiculaire à toutes les droites du plan ? ………… C’est ce que nous allons mettre en évidence maintenant…. |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
Fiche 7 : Droite perpendiculaire à un plan . |
|
||||||||||
|
|
|
|
||||||||||
|
|
Définition : Dire
qu’une droite est perpendiculaire à un plan c’est dire qu’elle est
perpendiculaire à toutes les droites de ce plan. |
|
||||||||||
|
|
|
|
||||||||||
|
|
|
|
||||||||||
|
|
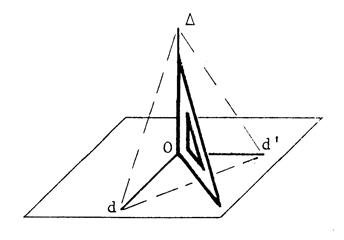
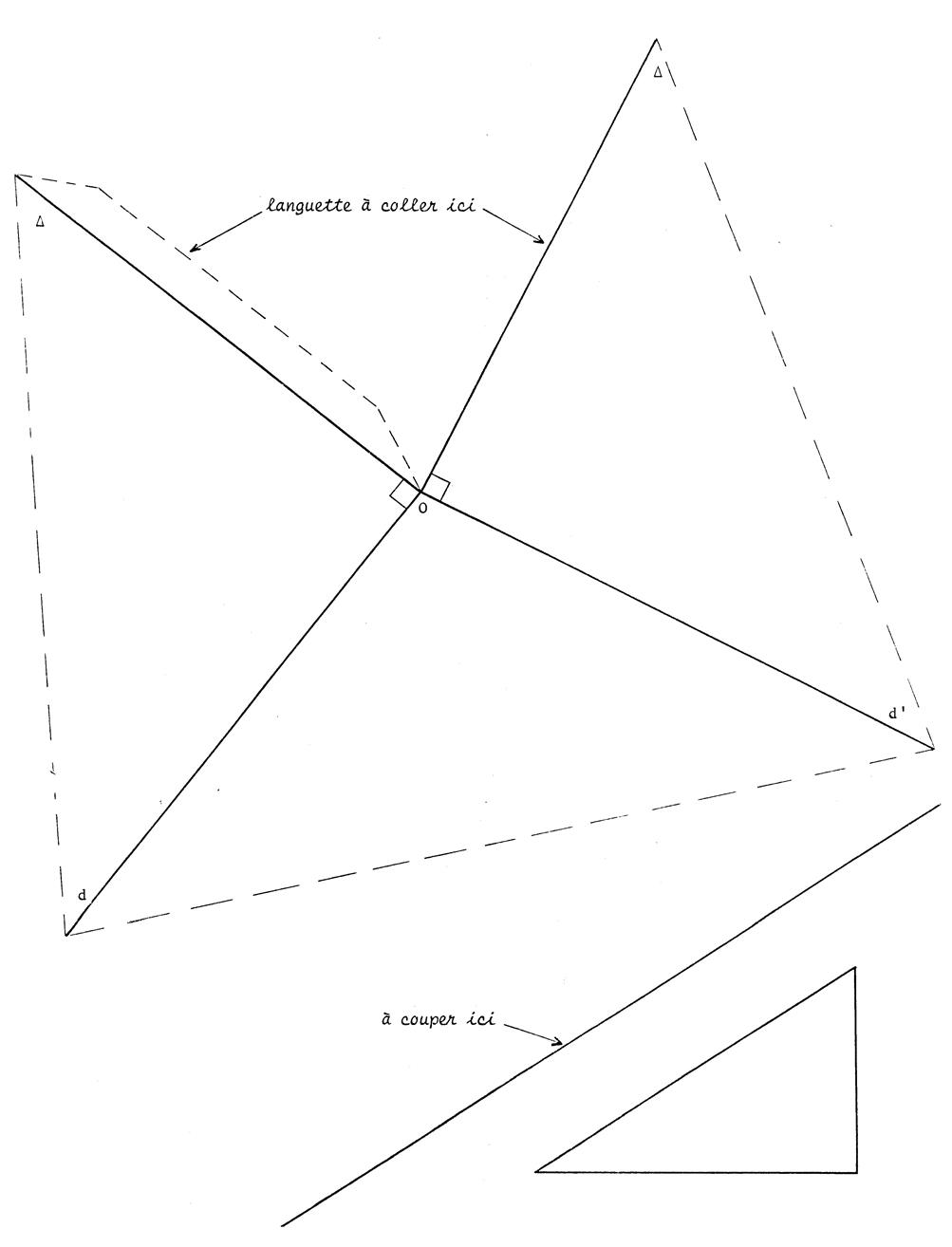
Prendre la « FICHE
7 bis » On a dessiné deux droites « d »
et « d’ » sécantes en « O ». On
a tracé par « O » la perpendiculaire à « d » et la
perpendiculaire à « d’ ». Découpez
cette figure suivant les pointillés et une portion de « Pliez
suivant la droite « d » et la droite « d’ » et pliez la
languette puis collez la languette de telle sorte que la perpendiculaire en
« O » à « d » coïncide avec la perpendiculaire en
« O » en « d’ ». On
appellera « Découpez
l’équerre dessinée au coin de la page « FICHE 7
bis » et à l’aide de celle-ci
, contrôlez que « On
dira alors ( il
est possible de le démontrer ) .’ |
|
|
|||||||||
|
|
Théorème : Si une droite perpendiculaire à deux droites
sécantes d’un plan alors elle est perpendiculaire à toutes les droites de ce
plan. (On dit alors , par définition,
qu’elle est perpendiculaire au plan ). |
|
||||||||||
|
|
Conséquence : pour démontrer qu’une droite
est perpendiculaire à un plan , il suffit de prouver qu’elle est perpendiculaire à
deux droites sécantes de ce plan. |
|
||||||||||
|
|
|
|
||||||||||
|
|
Fiche 8 : Calculs dans le cube. |
|
||||||||||
|
|
|
|
||||||||||
|
|
« ABCDEFGH » est un cube de 6 cm
d’arête. 1°) Démontrez verbalement que « DBFH »
est un rectangle. Utilisez le théorème de la fiche « 7 »
et la propriété : Si deux droites sont perpendiculaires à un plan
alors elles sont …………….…… |
|
|
|||||||||
|
|
2°) Calculons
« DB » ; « DF » ; et « HB » . [ DB ] est la diagonale du carrée « ABCD » , donc « DB =
……….. » ; [ DF ] et [ HB ] ;sont les diagonales de
« DBFH » , donc « DF = HB= 3° ) [ DF ] et [ HB ] se coupent en
« O ». Démontrons que « O » est le milieu
de [ DF ] , [ HB ] , [ AG ] et [ EC
] et que « DF = HB = AG = EC ». « DEFH » étant rectangle ses diagonales
[ DF ] et [ HB ] se coupent en leur ..milieu…et
ont même longueur . |
|
||||||||||
|
|
On démontre
de même que « DAFG » est un rectangle ainsi que …………………………… Donc ………………et ………………… ont même milieu et ont même
longueur ainsi que …………………..et ……………………. |
|
||||||||||
|
|
|
|
||||||||||
|
|
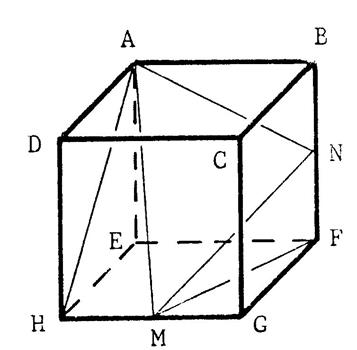
4°) « M » est le milieu de [ HG ] et « N » est le milieu de [ BF
] . Calculez « AN». 5°) Démontrez que « MHA » est un
triangle rectangle et calculez AM . |
|
|
|||||||||
|
|
6°) Démontrez que « NFM » est un
triangle rectangle et calculez MN . |
|
||||||||||
|
|
|
|
||||||||||
|
|
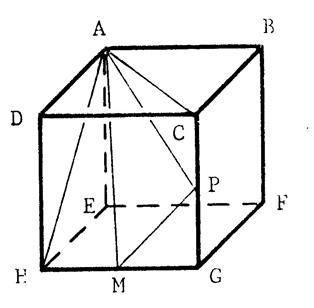
7°) Le triangle « AMN » est-il
rectangle ? 8°) « P » est le milieu [ CG ] . Démontrez que « APM » est isocèle. |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
9°) « R » est le milieu de [ DH ] . En utilisant le rectangle « DBFH » , calculez « RN ». 10°) Démontrez que « RMN » est un
triangle rectangle. |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
Fiche 9 : Situations problèmes. |
|
||||||||||
|
|
|
|
||||||||||
|
|
Problème
1 : |
|
||||||||||
|
|
« ABCD » est un rectangle dont les
dimensions sont « 15 cm » et « 20 cm ». « H » est le projeté orthogonal de
« A » sur ( DB) . 1°) Calculer « BD ». 2°) Calculez l’aire du triangle « ABD »
et déduisez – en « AH ». 3°) Calculez « DH » et
« HB ». |
|
||||||||||
|
|
Problème
2 : |
|
|
|||||||||
|
|
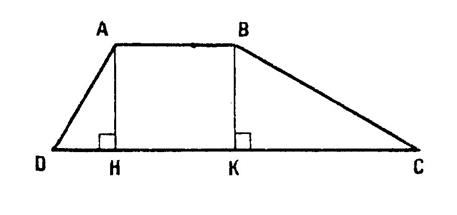
« ABCD » est un trapèze , ( AB
) // ( CD ) , [ AH ] et [ BK ] sont des hauteurs. « AD = 10 cm » , « AB = 10 cm » , En utilisant le fait que “ADH” et “BCK” sont des demi- triangles
équilatéraux. Calculez : « DH » , « AH »
, « BC » , « KC » , « DC » et « AC ». Donnez les valeurs exactes puis les valeurs
approchées à 10 -2
près. |
|
|
|||||||||
|
|
Problème
3 : |
|
|
|||||||||
|
|
« DEF » est un triangle isocèle . « DE = EF = 50 cm » et « DF = 80 cm ». Les médianes [ EH ] et [
DK ] et [ FL ] se coupent en « G ». Calculez la longueur de chacune des médianes. ( Utilisez la propriété du centre de gravité) |
|
|
|||||||||
|
|
|
|
|
|||||||||
|
|
Problème
4 : |
|
|
|||||||||
|
|
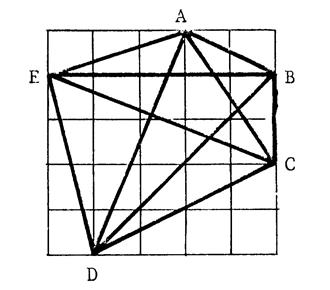
Les côtés des carrés du quadrilatère ci-contre ont
pour longueur « 1 cm ». ( Echelle 0,8) Déterminez par le calcul la longueur de tous les
segments de la figure qui ont un nom. Rangez ces segments dans l’ordre de longueur
croissante. |
|
|
|||||||||
|
|
Problème
5 : |
|
|
|||||||||
|
|
Une sphère a « 6 m » de rayon. Elle est
coupée par un plan dont la distance au centre de la sphère est de
« 3m ». Vous savez que l’intersection est un cercle.
(voir le cours @). Quel est le diamètre de ce cercle à
« 1cm » près ? |
|
|
|||||||||
|
|
Problème
6 : |
|
|
|||||||||
|
|
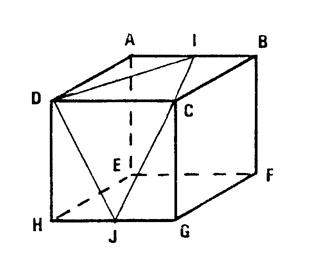
« ABCDEFGH » est un cube dont l’arête est « 10m ». « I » est le milieu de [ AB ] et
« J » est le milieu de [ HG
]. Calculez
« ID » , « IC » ,
« JD » , « JC ». Dites en l’expliquant si « DICJ » est
un losange. |
|
|
|||||||||
|
|
Problème
7 : |
|
|
|||||||||
|
|
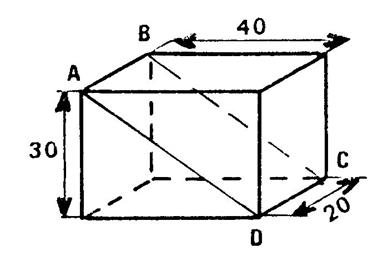
Une boîte parallélépipédique s’ouvre en
séparant deux parties coupées suivant
la ligne polygonale « ABCD ». Quelle longueur de ruban adhésif faut-il pour la
fermer totalement le long du tracé « ABCD » ? ( unité le cm). (D’après le brevet de Nantes 1987) |
|
|
|||||||||
|
|
Problème
8 : |
|
|
|||||||||
|
|
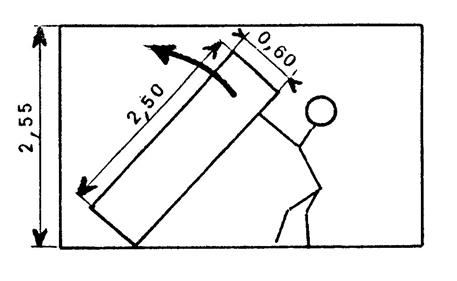
Dans
une pièce de 2,55 m de hauteur, on veut relever un meuble de forme
parallélépipédique de 0,60 m de profondeur et d’une hauteur de 2,50 m en procédant comme indiqué sur le dessin
ci-contre. Est-ce possible ? ( Brevet
Montpellier 1987) |
|
|
|||||||||
|
|
Problème 9 : |
|
|
|||||||||
|
|
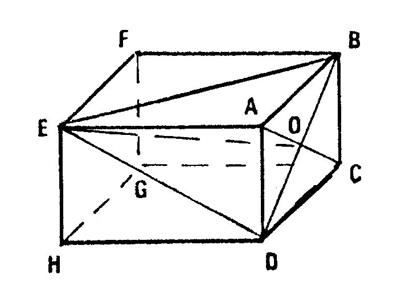
« ABCDEFGH » est un parallélépipède rectangle de « 8
cm » de longueur. « ABCD » est un carré de « 4
cm » de côté et de centre « O ». 1°) Calculez « BD » ,
« DE » , « EB ». 2°) Quelle est la nature du triangle
« EBD » ? 3°) Démontrez que (EO) n’est pas perpendiculaire à (BD ) . 4°) Expliquez pourquoi (EO) n’est pas
perpendiculaire au plan « ( ABCD). Calculez « EO » de deux façons et
calculez « EC ». ( Brevet Poitiers 1987) |
|
|
|||||||||
|
|
|
|
|
|||||||||
|
|
|
|
||||||||||
|
FICHE 7 bis |
|
|
|
|
|
|
|
|
CONTROLE
|
|
|
|
|
|