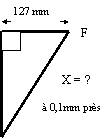DOSSIER N° : CORRIGE PYTHAGORE

CONTROLE CORRIGE

a ) Qu ‘appelle -t- on « grandeur » ?

on appelle « grandeur » tout nombre associé à une unité.

b) Qu’appelle - t- on « carré d’un nombre » ?

On appelle « carré » d’un nombre , le produit d’un nombre par lui même.

a) Comment reconnaît - on l’hypoténuse d’un triangle rectangle ?

L’ hypoténuse est le plus long coté du triangle.

I ) Dans quelle est la condition d’application du théorème de Pythagore ?

« Pythagore » ne s’applique qu ’ au triangle rectangle dont on connaît deux valeurs ( longueurs) sur trois.

II ) Enoncer le théorème de PYTHAGORE :

Dans un triangle rectangle , le carré de la longueur de l’hypoténuse est égal à la somme des carrés des cotés formant l’angle droit.

III ) A partir de l’énoncé précédent mettre sous forme d’une égalité mathématique avec comme figure géométrique le triangle suivant :

a

	A
				b
B			C

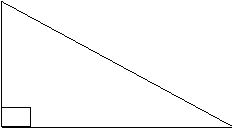
AC² = AB ² + BC ² c² = a² + b²

IV ) Soit l’égalité mathématique : a² = b² + c²

trouver « a = » puis « b = »  et « c = »  par transformation de l’égalité , indiquer les étapes successives.

Calcul de « a »

si a² = b² + c² alors a =  ;

Calcul de « b »

si a² = b² + c² alors a² - c² = b² ; donc b =

Calcul de « c »

si a² = b² + c² alors a² - b² = c² ; donc c =

V ) Soit DF² = DC² + CF² ; trouver DF ; DC ; CF par transformation de l’égalité ( indiquer les étapes successives)

Calcul de « DF »

si DF² = DC² + CF²  ; alors DF=  ;

Calcul de « DC »

si DF² = DC² + CF² ; alors DF² - CF² = DC² ; donc DC =

Calcul de « CF »

si DF² = DC² + CF²  ; alors DF² - DC² = CF² ; donc CF =

EVALUATION : CORRIGE

Calculer dans les cas suivants la ou les valeurs suivantes :

				C
									T
		108 mm

x = 117 mm

x = 201,2 mm

							B
								C
		C	H	B
		AB : 110mm ;AC = 93,5 mm
28900+ 9025=........ d = 194,7cm		Calculez : AB = « x » ( à 1 mm près) AC = « y » ( à 1 mm près)
						1024+1024 ; « d »=453cm

^{ABCD est un rectangle}

d

C

D

B

A

 ^{; « d » la diagonale.}

AB = 170 cm ; BC =95cm

^{Calculer AC = « d » (à 0,1 cm près)}

^{CH = 43 cm ; HB = 71 cm ; h = 83cm}

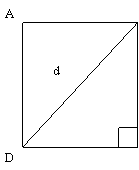
^{BC = 32 dm}

^{ABCD est un carré ; « d » est la diagonale ;}

^{BD = « d » ; calculer « d » à 1 cm près.}

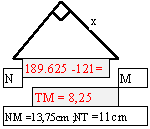
D

Sachant que DC =31 m ;CB 33 m ;

et BA = 56 m ;

Calculer AC = ?

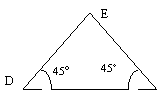
AD = ? (à 0,1 m près )

Angle E = 180°- (45°+45°) =90°

Le triangle DEF est rectangle isocèle

DE=EF=160cm

DF=2263mm

EF = 160 cm

Calculer l’angle E :

Que peut-on dire du triangle DEF ?

Calculer : DE ; DF (au mm près)

^aangle

		F