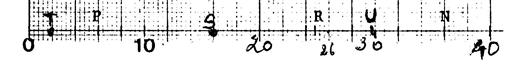|
|
Classe 5ème collège. |
|
|
· Translation ( notion)(coordonnées
et déplacement) |
|
|
|
· Informations
sur : Les principales façons de
repérer un point |
Corrigé des fiches de travail …. |
|
|
· Repérage
d’un point dans un repère
cartésien ou non cartésien (exemples) |
||
|
· Info : Projection d'un point sur une droite |
||
Environnement du dossier:
DOSSIER :
( CORRIGE de
) REPERAGE D ' UN POINT et
Représentation graphique.
|
|
Fiche 1 : Demi-droite graduée. |
|
|
|
Fiche 2 : Choix d’une unité sur une droite
graduée. |
|
|
|
Fiche 3 : Repérage d’un point dans le plan. |
|
|
|
Fiche 4 : Représentation graphique- Choix des unités |
|
|
|
Fiche 5 : Repérage sur une carte. |
|
|
|
Fiche 6 : Utilisation d’une représentation
graphique. |
|
|
|
|
Travaux auto
formatifs et devoir formatif |
|
A
faire : |
|||
|
TEST |
COURS |
|
|||||
COURS
|
|
Fiche 1 : Demi-droite graduée. (De
la gauche vers la droite dans l’ordre croissant ) |
|
|||||||||||||||||||||||||||||||
|
|
Exemple 1 : Voici ci-dessous une demi-droite
graduée ( plus précisément : régulièrement graduée). 1 cm représente l’unité , donc 1
mm représente 0,1 unité. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Le point « O » est appelé
« l’origine », on lui fait correspondre le nombre « 0 » ( dire : zéro
). Au point « B » ,
on a fait correspondre le nombre « 5 ». On dit que « 5 »
est l’abscisse de « B ». Quelle est l’abscisse de « A » ? …9.. ;
de « C » ? …13,5…. ; de « D » ? …3,3……., ; de
« E » ? …7,5….. |
|
|||||||||||||||||||||||||||||||
|
|
Activité n° … : Placez les points
« F » ; « G » ; « H » ;
« K » d’abscisses
respectives
« 11 » ; « 6,5 » ;
« 14,8 » ; « 0,75 » |
|
|||||||||||||||||||||||||||||||
|
|
Corrigé
ci-dessous : |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Exemple 2 : Voici ci-dessous une demi-droite
graduée , l’unité est représentée par un segment de 2 cm. Alors : 1 cm représente …0,5 .unité ;
1 mm représente ……1/20…d’.unité . |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Activité n° : Quelle est l’abscisse de « K » ? …7.. ;
de « L » ? …1,5…. ; de « M » ? …5,8……., ; de
« N » ? …4,15….. ; de
« V » ? …2,9….. Activité n° … : Placez les points
« P » ; « R » ; « S » ;
« T» ; « U »
d’abscisses respectives « 8 » ;
« 2,5 » ; « 6,3 » ; « 0,25 » ;
« 3,625 » |
|
|||||||||||||||||||||||||||||||
|
|
Corrigé ci-dessous : |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Exemple 3 : Voici ci-dessous la demi-droite
graduée , le point d’abscisse « 2 » est déjà placé.
· 10 cm représente « 2 » unités, donc « 1 cm »
représente …0,2….. unité ; « 1
mm » représente …0,02. Unité · Nous avons écrit ci-dessous
l’abscisse des points principaux de la graduation ( tous
les 1 cm) , placez ceux manquants.(0,8 ;
1,4 ; 1,6 ;1 ;8 ) |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Activité n° : Quelle est l’abscisse de « A » ?
……….. de « B » ?
………………… de « D » ? ………………….. ; de
« C » ?............ Activité n°…. Placez les points « F » ;
« G » , « H », « J »
d’abscisses respectives
« 0,8 » ; « 1,9 » ; « 0,48 »
, « 1,09 ». |
|
|||||||||||||||||||||||||||||||
|
|
Corrigé ci-dessous : |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Activités : |
|
|||||||||||||||||||||||||||||||
|
|
Dans chacun des cas ci-dessous
, en tenant compte des abscisses déjà placées , écrivez l’abscisse des
points principaux de la graduation ( tous les 1 cm). Complétez les demi-droites en donnant l’abscisse des points désignés
par une lettre et placez sur la droite le nom des points dont on donne
l’abscisse. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
M |
N |
P |
R |
S |
T |
|
|||||||||||||||||||||||||
|
|
7 |
2,8 |
5,4 |
0,9 |
0,42 |
0,075 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
U |
V |
W |
X |
Y |
Z |
|
|||||||||||||||||||||||||
|
|
100 |
840 |
365 |
1 000 |
690 |
255 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
A |
B |
C |
D |
E |
F |
|
|||||||||||||||||||||||||
|
|
150 |
10 |
237,5 |
75 |
220 |
57,5 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
G |
H |
J |
K |
L |
M |
|
|||||||||||||||||||||||||
|
|
16 |
6,8 |
2 ,3 |
12 |
5 |
18,5 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
N |
P |
R |
S |
T |
U |
|
|||||||||||||||||||||||||
|
|
36 |
60 |
24,8 |
16 |
2 |
29,2 |
|
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Fiche 2 : Choix d’une unité sur une droite
graduée. |
|
|||||||||||||||||||||||||||||||
|
|
Voici la portion de droite graduée dont on
dispose. Sa longueur est de 100 mm. Le plus grand nombre que l’on ait à placer est
« 173 ». Quelle unité faut-il choisir afin que
« 173 » soit le plus à droite possible ? |
|
|||||||||||||||||||||||||||||||
|
|
· « 173 » est voisin de « 200 » . · Donc « 100 mm » représente « 200 ». · Donc « 1 mm » représente …2..unités. Ainsi , écrivons l’abscisse des points principaux ( tous les 1 cm)et plaçons
le point d’abscisse « 173 ».
|
|
|||||||||||||||||||||||||||||||
|
|
Activités :
faites de même dans les exercices ci-dessous : · Donnez le nombre d’unités correspond à « 1 mm » · Ecrivez l’abscisse des points principaux ( tous
les 1 cm) · Placez le point dont on donne l’abscisse. |
|
|||||||||||||||||||||||||||||||
|
|
Activité .. Plus grand nombre à placer
« 465 » |
|
|||||||||||||||||||||||||||||||
|
|
« 465 » est voisin de « 500 ».
Donc « 100mm » représente 500 . Donc 1 mm représente « 5 »
unités. ( 2
cm = 100 u ; 1 cm = 50 u ; 1 mm = 50 /10)) |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Activité .. Plus grand nombre à placer
« 23,5 » |
|
|||||||||||||||||||||||||||||||
|
|
« 23,5 » est voisin
de « 25 »
. Donc « 100 mm » représente
« 25 u. » . Donc 1 mm représente «
25/ 100 » soit 0,25 unité. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Activité .. Plus grand nombre à placer
« 3,8 » |
|
|||||||||||||||||||||||||||||||
|
|
« 3,8 » est proche de
« 5 » . Donc « 100mm »
représente « 5 u » . Donc « 1 mm » représente « 5 / 100 = 0,05 » unité. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Fiche 3 : Repérage d’un point dans le plan. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
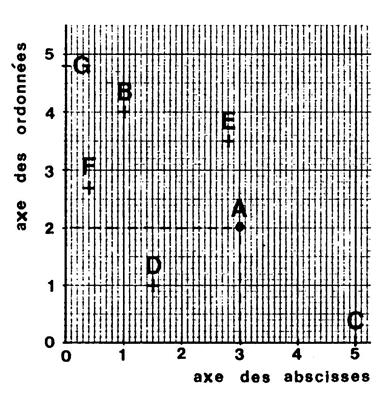
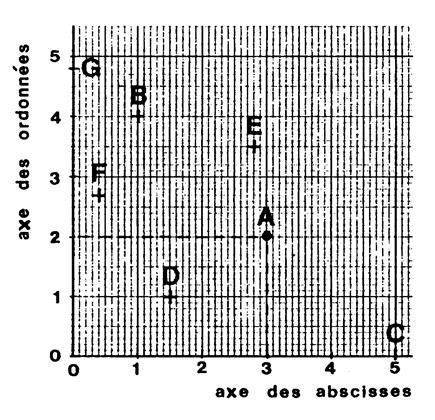
Ci-contre on vous a représenté deux
demi-droites graduées perpendiculaires
et de même origine. · Le point « A » est repéré par le couple de
nombres ( 3 ; 2 ) · « 3 » est appelé « l’abscisse » de
« A ». · « 2 » est appelé « l’ordonnée »
de « A ». · Le couple (
abscisse ; ordonnée) est appelé « le couple de coordonnées
du point.». · Les droites graduées sont
appelées : « axe des abscisses » et « axe des ordonnées », on dit
aussi « axe des coordonnées » . |
|
|
||||||||||||||||||||||||||||||
|
|
Activité : ………..A partir du graphe
ci-dessus :
Relevez et Donnez le couple de coordonnées des points |
|
|||||||||||||||||||||||||||||||
|
|
B ( 1 ; 4 ) |
C ( 5 ; 0) |
D ( 1,5 ; 1) |
E ( 2,8 ; 3,5) |
F ( 0,4 ; 2,7) |
G ( 0 ; 4,8) |
|
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
B ( … ; …) |
C ( … ; …) |
D ( … ; …) |
E ( … ; …) |
F ( … ; …) |
G ( … ; …) |
|
||||||||||||||||||||||||||
|
|
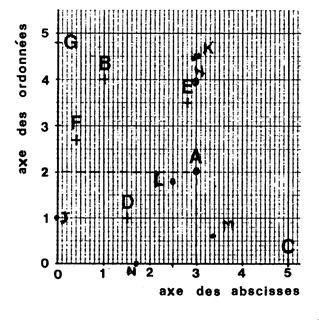
Activité : ……….Placer les points dont on
donne les coordonnées : |
|
|||||||||||||||||||||||||||||||
|
|
H ( 3 ; 4) |
J ( 0 ; 1) |
K ( 3 ; 4,5) |
L ( 2,5 ; 1,8) |
M ( 3,4 ; 0,6) |
N ( 1,7 ; 0) |
|
||||||||||||||||||||||||||
|
|
Corrigé
|
|
|||||||||||||||||||||||||||||||
|
|
Fiche 4 : Représentation graphique- Choix des
unités. |
|
|||||||||||||||||||||||||||||||
|
|
Dans chacun des exemple
ci-dessous, on donne « 2 » axes de coordonnées. A vous de faire la représentation graphique
correspondant au tableau. Pour cela, choisissez convenablement les unités
sur les axes, placez les points de joignez ces points par une courbe
régulière. Y-a-t-il des cas où on peut parler de
proportionnalité ? ……………OUI……….. Dites comment on peut le reconnaître sur le
graphique ou sur le tableau…. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Activité : |
|
|||||||||||||||||||||||||||||||
|
|
Axe des abscisses |
0 |
0,2 |
0,5 |
1 |
2 |
3,4 |
4,5 |
8 |
|
|||||||||||||||||||||||
|
Axe des ordonnées |
0 |
0,6 |
1 |
1,4 |
2 |
2,6 |
3 |
4 |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
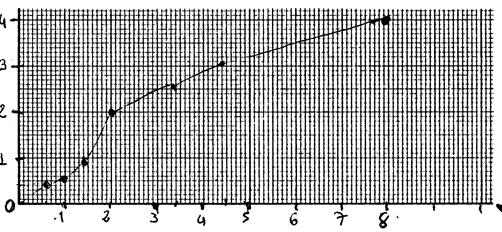
Activité … : |
|
|||||||||||||||||||||||||||||||
|
|
Axe des abscisses |
0 |
5 |
12 |
19 |
25 |
32 |
40 |
45 |
|
|||||||||||||||||||||||
|
Axe des ordonnées |
0 |
0,1 |
0,24 |
0,38 |
0,5 |
0,64 |
0,8 |
0,9 |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Corrigé
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
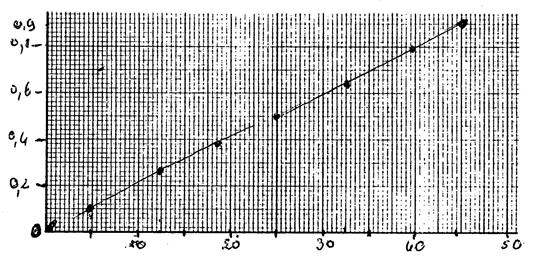
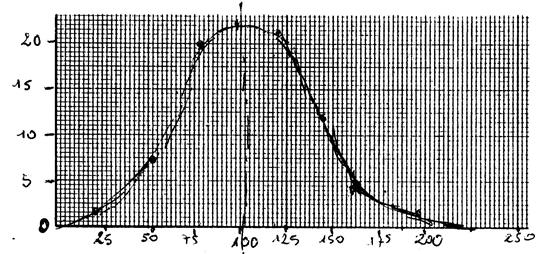
Activité ….. : |
|
|||||||||||||||||||||||||||||||
|
|
Axe des abscisses |
20 |
50 |
76 |
100 |
120 |
142 |
160 |
200 |
|
|||||||||||||||||||||||
|
Axe des ordonnées |
1,5 |
7,5 |
20 |
22,5 |
21 |
11 |
4,5 |
0,5 |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Dans cette situation la courbe à tracer admet un
axe de symétrie. Vous pouvez utiliser d’autres points pour tracer la courbe. |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Fiche 5 : Repérage sur une carte. |
|
|||||||||||||||||||||||||||||||
|
|
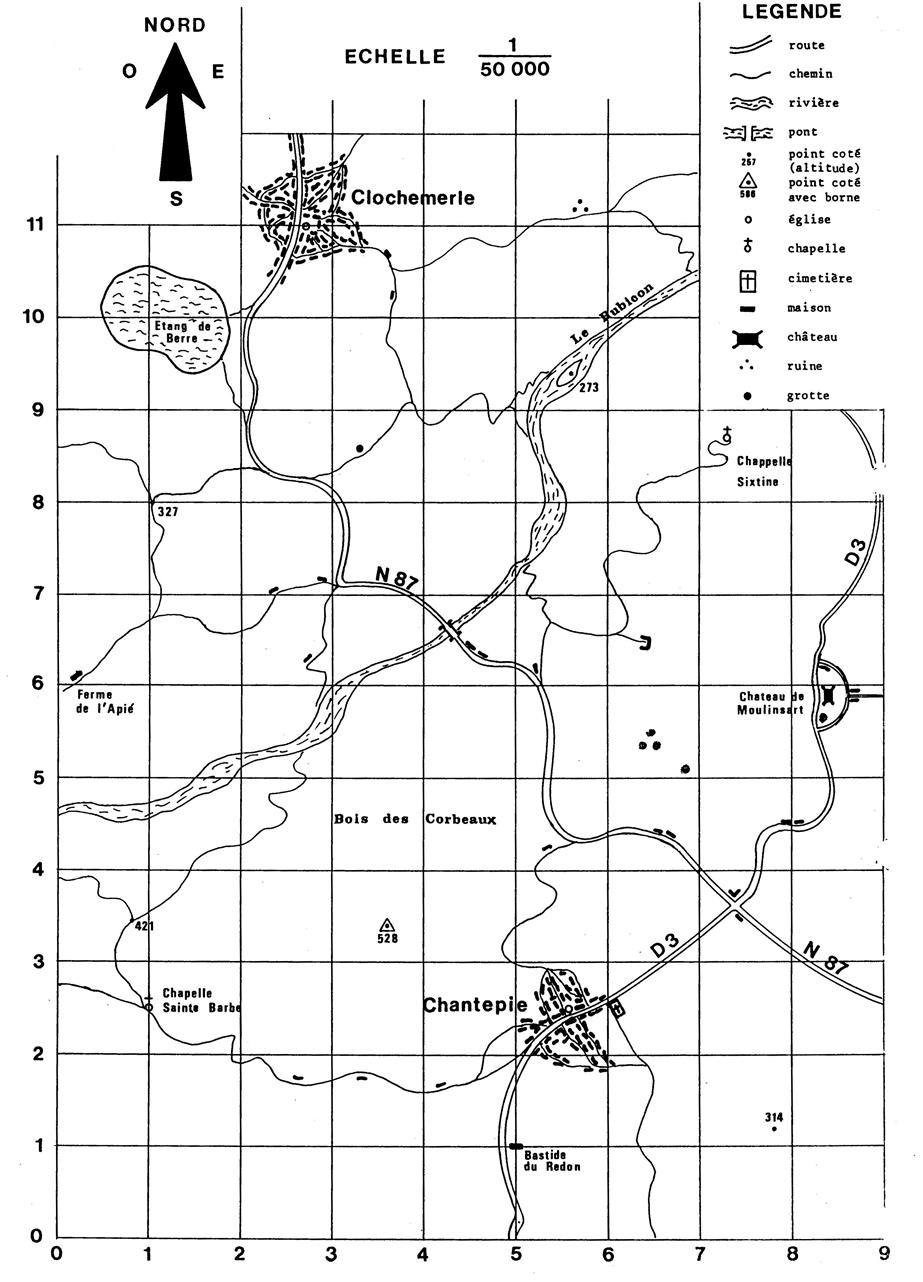
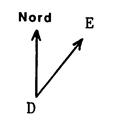
Soit la carte ci-dessous : Cette carte est à
l’échelle
Sur cette carte, on a tracé un quadrillage. Mesurez le côté des carrés de ce quadrillage,
vous trouvez …2 cm. Sur le terrain, les carrés
correspondants ont …1..km de côté. |
|
|||||||||||||||||||||||||||||||
|
|
Ce quadrillage sert à repérer les points de la
carte ( donc du terrain) L’axe des abscisses a la direction OUEST-EST et
le sens croissant de OUEST vers EST. L’axe des ordonnées a la direction SUD- NORD et
le sens croissant de SUD vers NORD. Dans ca paragraphe , on
donnera les coordonnées avec « 1 » chiffre après la virgule. Exemple : Point A : Eglise de Clochemerle :
A ( 2,7 ; 11,0 ) Point
B : Carrefour de la nationale N87 et de la départementale
« D3 » : B ( 7,4 ; 3,6) |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
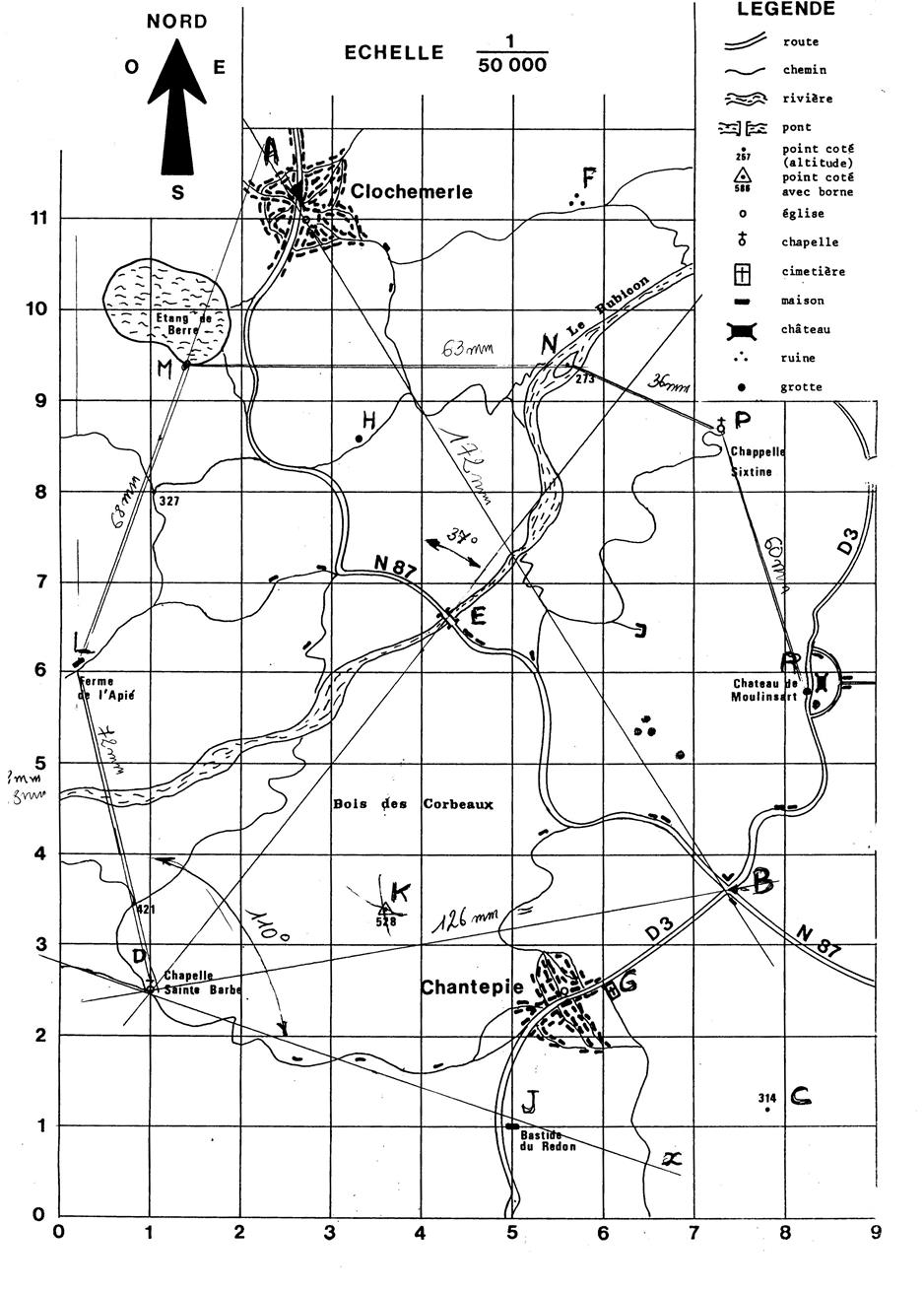
Corrigé :
|
|
|||||||||||||||||||||||||||||||
|
|
Activité : …….. On vous donne les coordonnées des points
suivants : |
|
|||||||||||||||||||||||||||||||
|
|
· Point C : Point coté 314 ( au sud du
point « B » |
C
( …7,8… ; …1,2….) |
|
||||||||||||||||||||||||||||||
|
· Point « D » : Chapelle Sainte Barbe (
Sud- Ouest de la carte) |
D ( …1.. ;
…3,5….) |
||||||||||||||||||||||||||||||||
|
· Point « E » : Pont ( passage
de N87 sur le Rubicon. |
E ( …4,3… ;
6,6 ) |
||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Activité : …….. On vous donne la description des points dont on
donne les coordonnées ( regardez la légende ). |
|
|||||||||||||||||||||||||||||||
|
|
· Point F ( 5,7 ;
11 , 2 ) |
………ruine ……………… |
|
||||||||||||||||||||||||||||||
|
· Point G ( 6,1 ; 2, 5 ) |
………cimetière………… |
||||||||||||||||||||||||||||||||
|
· Point H (
3,3 ; 8 , 6 ) |
…………grotte ……………… |
||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Activité : …….Calcul sur la
Distance |
|
|||||||||||||||||||||||||||||||
|
|
Déterminez la distance à vol d’oiseau ( c'est-à-dire en ligne droite ) de « D » à
« B » : Sur la carte à « 1 mm » prés : …126………mm. Sur le terrain
en « km » à 100 m près : 6,3 km. Même question pour « AB ». Sur la
carte : 172 .mm.
Sur le terrain à « 50 m prés » :…8,6..km. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Activité : …….Tracé géométrique : Tracez la demi-droite [ DE . Mesurez l’angle que fait cette demi-droite avec
la direction SUD-NORD ( sur la carte). Vous trouvez : …37°….. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
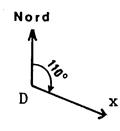
Activité ……Positionner d’un point ….. : Partant de « D3 tracez la demi-droite | D x
qui fait avec la direction « SUD-NORD » un angle de 110°. Donnez les coordonnées et la description du point
« J » situé sur cette demi-droite à « 4,25 km » de « D ». J ( …5.. ;…1 …) ; 85 mm , bastide du redon |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Activité …… |
|
|||||||||||||||||||||||||||||||
|
|
Donnez les coordonnées et la description du point
« K » situé à l’ouest de la « N87 » et à la fois à
« 3,8 km » de « B » et « 3,25 km » de
« E ». K ( 3,6… ;…3,5
..) , point de cote avec altitude (
3,7 km = 76 mm et 3,25 km = 65 mm ) tracez 2 arcs de cercle avec un compas .. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Situation - Problème. |
|
|||||||||||||||||||||||||||||||
|
|
Un oiseau parcourt en ligne droite l’itinéraire
décrit ci-dessous. Tracez cet itinéraire sur la carte. Donnez les coordonnées
des différents points et calculez la longueur
totale de l’itinéraire. L’oiseau part du point « D » ( Chapelle Sainte Barbe) , il passe par le point
« L » : »ferme de l’Apié »
situé à environ 4 km au nord de « D » : L ( 6,1… ; 0,2…) Il prend ensuite une direction qui fait avec la
direction SUD-NORD un angle de « 21° » pour arriver au point « M » situé
au bord de l’Etang de Berre , côté sud : M ( …1,3… ;…9,5 ..) IL vole
ensuite plein Est jusqu’au point côté « 273 » situé dans une
ile de la rivière « Le Rubicon » :
N ( …5,6… ;…9,5 …) . IL franchit le Rubicon pour aller à la chapelle sixtine : P ( 7,2… ; 8,7 …) Puis il fait « 3 km »
pour arriver au point « R » situé au bord de la route
départementale « D3 » : R ( 8,2…. ; 5,8….) . |
|
|||||||||||||||||||||||||||||||
|
|
La longueur du trajet parcouru par l’oiseau
est de : 72 + 68 + 63+ 36 + 60 = 299 mm
soit une distance de 299 fois 50 000 = 14 950 000 mm=
14,950 km |
|
|||||||||||||||||||||||||||||||
|
|
Fiche 6 : Utilisation d’une représentation
graphique. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Considérons tous les rectangles dont le périmètre
est de « 20 cm » . On vous demande d’exprimer l’aire de ces
rectangles en fonction de leurs dimensions. Appelons « Le périmètre étant égal à 20 cm
, le demi-périmètre est égal à ……10……cm. ( ½ P = 20 / 2 = 10 ) ; ( La mesure ( en cm) de
l’autre dimension est donc « La mesure en « cm² » de l’aire
correspondante est alors : |
|
|||||||||||||||||||||||||||||||
|
|
Activité : Complétez le tableau donnant
l’aire correspondant à certaines valeurs de « |
|
|||||||||||||||||||||||||||||||
|
|
« |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
||||||||||||||||||||
|
Aire ( en cm²) |
0 |
9 |
16 |
21 |
24 |
25 |
24 |
21 |
16 |
9 |
0 |
||||||||||||||||||||||
|
|
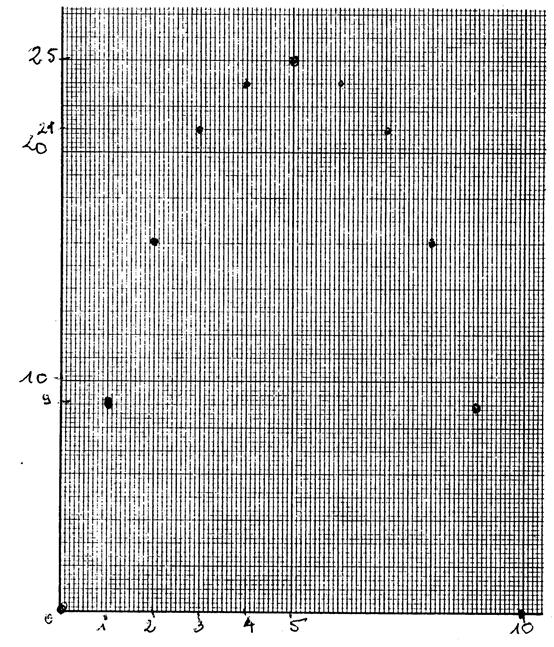
Faites la représentation
graphique correspondante. Pour cela, placez les points
dont les coordonnées sonr données dansle tableau et joingnez ces points par
une courbe régulière. ( choissisez bien les unités) |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Corrigé : on place les points.. |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
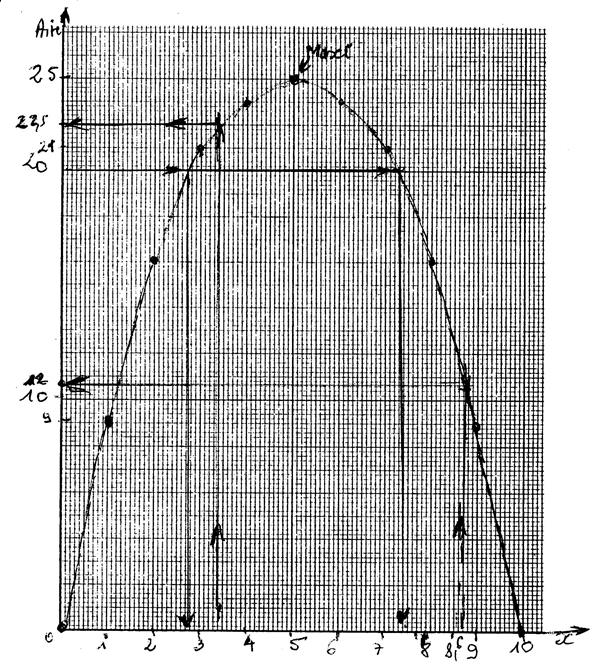
Corrigé : on joint les points.., on peut observer la position
de l’axe de symétrie parallèle à l’axe des « y ».
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
TRAVAUX AUTO
FORMATIFS.
Faire toutes les activités ci-dessous !!!
Compléter le dessin : Dites tout ce que vous savez sur l'image ci dessous
.
|
|
v Qu ‘ appelle -t - on « coordonnées d’un
point » ?
v Comment appelle t - on l’axe des
« x » ?
v Axes des abscisses
v Comment appelle t - on l’axe des
« y » ?
Axes des ordonnées
v Sur quel « axe » trouve t - on les
« ordonnées » ? l’axe des « y »
v Sur quel « axe » trouve t - on les « abscisses »
? l’axe des « x »
v Donner la procédure à utiliser pour trouver
les coordonnées d ’ un point dans un repère orthonormé.
v Procédure permettant de trouver les
coordonnées d ’ un point dans un plan :
v Pour trouver les coordonnées d’un point dans
un plan :
v « on projète
l’image du point sur les deux axes »
v Il faut tracer une droite parallèle à l ’ axe
des ordonnées (y’y) pour trouver la valeur de l ’ abscisse et une autre droite
parallèle à l ’ axe des abscisses (x’x) pour trouver la valeur de l ‘ordonnée.
v
EVALUATION :Voir Contrôle Continu Fiche situation
@ 5
1°) Dans un repère ( O , ![]() ,
, ![]() ) placer les deux points suivant A ( 1 ; 2 ) et B ( -3 ; 4 )
) placer les deux points suivant A ( 1 ; 2 ) et B ( -3 ; 4 )
2°)Travail : citer
dix couples de décimaux positifs au plus
SUJET 3
|
TC2 |
E |
T |
C |
|
Repérage
d’un point dans un plan (P) muni d’un repère orthogonal ( O,I, J ) |
|
|
|
|
|
1°)
Déterminer les coordonnées des points : |
|
|
|
A (___) ; B (___) ; C (___) ;
D (___) ;E(___) ; F(___) ; O (___) ; J(___) |
|
|
|
2°)Placer
les points : P ( 0 ;+2,5) ; Q ( +1,5 ; 0) ; H (
-1 ; 0 ) ;N ( +3 ;-2) ; K ( +2 ; +4,5 ) ;L
(-4 ;-1) |
||