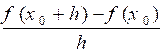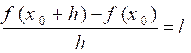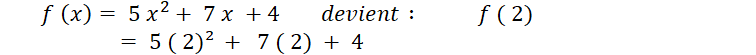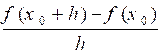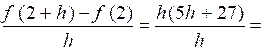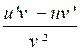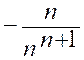Pré requis
2°)
Les fonctions (présentation) ![]()
ENVIRONNEMENT du dossier:
|
Objectif précédent Retour au cours sur
l’étude d’une fonction |
Objectif suivant : 1°)
Etude sur l’étude de la représentation graphique d’une fonction |
|
|
|
|
|
|||
|
|
RESUME sur L’ETUDE D’ UNE
FONCTION NUMERIQUE. : la dérivée
|
|
|||
|
|
|
|
|||
|
|
2. Fonction dérivée d’une fonction ;
3. Signe de la dérivée et sens de
variation de la fonction ; |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
1- Dérivée
en 1 point . |
|
|||
|
|
|
|
|||
|
|
Soit Soit «
|
|
|||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|||
|
|
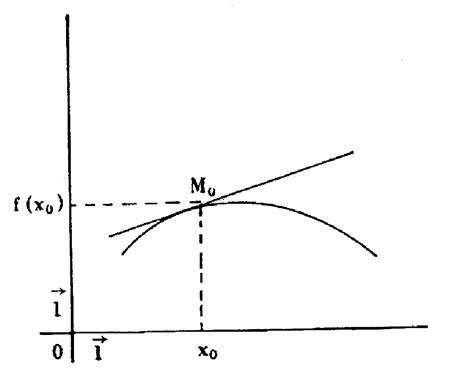
Notation : Interprétation
graphique : Pour qu’une fonction Le coefficient directeur de cette tangente
est égal à la dérivée de la fonction pour
Equation de la tangente : |
|
|||
|
|
|
|
|||
|
|
Equation
de la tangente : |
|
|
||
|
|
|
|
|||
|
|
Exemple : Soit la
fonction Travail demandé : -
Trouver la dérivée au
point -
Déterminer la tangente. |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Calcul de la
dérivée au point |
|
|||
|
|
-
Calcul de f ( x0
) ; pour
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
-
Calcul de : Ainsi :
Conclusion n°1 : la dérivée (dit
aussi : nombre dérivé) de la fonction
On peut ainsi calculer l’équation de la tangente
au point « x 0= 2 ) On sait que : On applique :
Conclusion n°2 : L’équation de la tangente au point « x 0= 2
) de la fonction f (x) = 5 x² + 7 x +4 ; est
y
= 27 x - 16 Note : Dérivée
et continuité :
si une fonction f admet
une dérivée en x 0 ( la réciproque n’est pas vraie) |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
2 - Fonction dérivée d’une fonction . ( info + Calcul
des dérivées.)
|
Soit |
Notation : f ‘
Par abus de langage,on dit souvent
« dérivée » au lieu de
« fonction dérivée » .
|
Valeur de la fonction f ( x) |
Valeur de la
dérivée f ( x) |
|
Fonction |
Dérivée. |
|
C
(constante) |
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Autres dérivées :
|
|
f |
|
f ‘ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
EXEMPLES :
( info +
sur le calcul des dérivées)
Calculer les dérivées des fonctions suivantes :
|
Valeur de la fonction f ( x) |
Valeur de la
dérivée f ( x) |
Résultat : |
Fonction type |
Dérivée type . |
|
f (x) = 3 x4
+ 2 x² + 3x + 4 |
f ’ (x) = 4 . 3 x4-1 + 2 .2 x²-1 + 3 + 0 |
f ’
(x) =
12 x3 +
4 x + 3 |
u +
v |
u
’ + v ‘ |
|
|
|
|
|
|
|
f (x) = ( x – 1)3 (
x + 2 ) 4 |
f ’ (x) = ? |
|
u
. v |
u
’ .
v + u . v ’ |
|
U = ( x – 1)3 , ou U
= u3 |
Avec
u = x – 1 |
U ‘ = 3 u ² u ‘ =
3 ( x – 1 )² |
Car u ‘ = 1 |
|
|
V = ( x + 2 ) 4 = v
4 |
avec v
= x + 2 |
V ‘ = 4
v 3 v ‘ = 4 ( x +2) 3 |
Car v ‘ = 1 |
|
|
|
|
|
|
|
|
On a alors : f ’ (x) = u’ v + u v ’ |
|
|
|
|
|
|
f ’ (x) = (( x – 1)3 ) (4 ( x +2) 3 )
+ ( ( x + 2 ) 4 ) (3 ( x – 1 )² ) |
|
|
|
|
|
f ’ (x) = (( x – 1 )² ) (( x +2) 3 ) [ 4 ( x – 1 ) + 3 ( x + 2 ) ] |
|
|
|
|
|
f ’ (x) = ((
x –
1 )² ) ((
x +2) 3 ) ( 7 x + 2 ) |
|
|
|
|
|
|
|
Voir : Calcul des dérivées. |
|
|
|
|
|
|
|
|
|
3 -
Signe de la dérivée et sens de variation de la fonction ;
Suivant le signe de la dérivée , on peut déterminer le sens de variation d’une
fonction :
-
Si la dérivée est nulle,
la fonction est constante.
-
Si la dérivée est positive dans un intervalle ] a , b [
, la fonction est croissante dans cette intervalle.
-
Si la dérivée est négative dans un intervalle ] a , b [
, la fonction est décroissante dans
cette intervalle.
(info plus @)
|
Un extremum local est
un point qui va déterminer où la
fonction va passer d’un accroissement à une diminution ( ou
inversement) |
Info @+
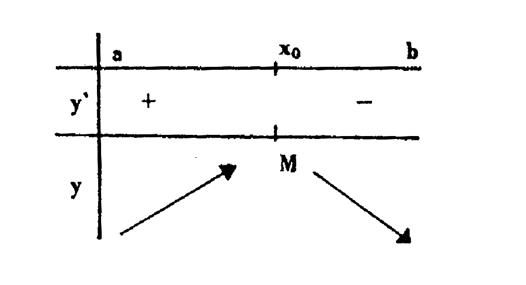
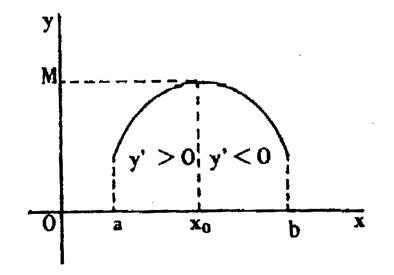
Maximum local : une fonction a un maximum local pour « x0 »
si elle cesse de croître pour décroître quand « x » traverse , en
augmentant , la valeur « x0 »,
donc si sa dérivée change de signe pour
« x » = « x0 » en passant du positif au
négatif.
|
|
|
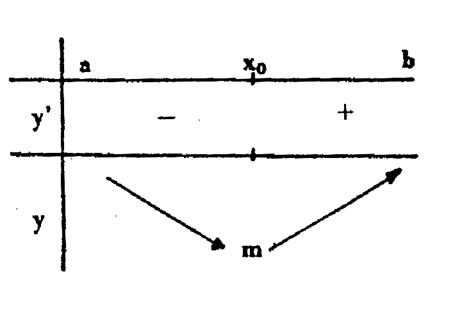
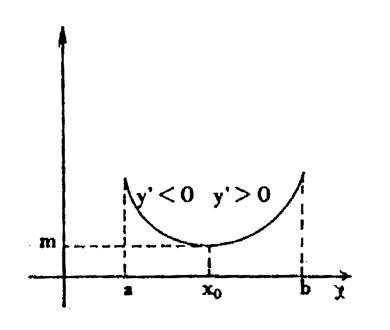
Minimum local : une fonction a un minimum local pour « x0 »
si elle cesse de décroître pour croître quand « x » traverse , en
augmentant , la valeur « x0 »,
donc si sa dérivée change de signe pour
« x » = « x0 » en passant du négatif au positif.
|
|
|