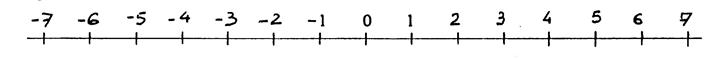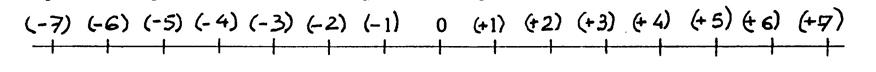|
|
|
Classe de 5ème |
|
|
|
|
|
|
|
|
|
||
|
|
|||
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
Objectif suivant 2°) Les égalités et « résoudre » 3°)( niveau 5 ) résolution des équations types du premier degré à une inconnue. |
DOSSIER : Les
égalités, les équations, les inégalités
|
|
|
|
|
|
Fiche
I : DEFINITIONS : EGALITES
et EQUATIONS. |
|
|
|
Fiche
2 : Résolution de la forme « a + x = b » |
|
|
|
Fiche
3 Comparaison de nombres relatifs. |
|
|
|
Fiche
4 : Nombres relatifs opposés. |
|
|
|
Fiche
5 : Règle de comparaison des nombres relatifs. |
|
|
|
||
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
Corrigé
Contrôle |
Corrigé
évaluation |
COURS
|
|
I ) DEFINITIONS : EGALITES et EQUATIONS. |
|
|
|
|
A ) égalité . |
|
|
|
|
« 3 +
8 = 11 » s’appelle une égalité. C’est une phrase mathématique. Cette phrase est
dite « vraie ». Le verbe de cette phrase est le signe « |
|
|
|
|
|
|
|
|
|
A retenir :
Une égalité est une phrase mathématique qui se présente sous la
forme : |
|
|
|
|
|
|
|
|
|
Remarque : Quand on écrit l’égalité : Exemple d’une égalité : Activité : on vous demande de vérifier ( à l’oral
si possible ) cette égalité . ( c'est-à-dire
que l’on vous demande de vérifier que cette phrase est vraie). Dans cette égalité , qui joue le rôle de « a » ? …………2 x 8 – 5 ……………………., qui joue le rôle de « b » ?
…………9 + 2 …………… |
|
|
|
|
B ) équation : |
|
|
|
|
v Soit la lettre « n » ,
« n » désigne un entier , Voici une phrase où figure le signe
« = » : n + 3 = 9 . Bien qu’il y ait le signe « = » , on ne peut pas dire que cette phrase soit une égalité
car elle peut être « vraie » ou « fausse » ; tout
dépend du nombre que l’on mettra à la place de « n ». Exemples : -
Remplaçons « n » par « 2 » . La phrase devient
2 + 3 = 9 , c’est une phrase …fausse…… -
Remplaçons « n » par « 6 » . La phrase devient
6 + 3 = 9 ; c’est une
phrase … vraie…… Aussi : -
« n » étant
un entier , n + 3 = 9 est appelée une équation d’inconnue « n ». -
« 6 » est appelée la solution de cette équation. -
« 2 » n’est
pas une solution de cette équation. |
|
|
|
|
Activité 1 : On vous donne une équation dans l’ensemble des
nombres relatifs :
( + 6 ) + y = ( - 7)
d’inconnue « y » Cherchez ( en faisant
des essais …….) une solution . Vous trouvez : y = ( - 13 )… |
|
|
|
|
|
|
|
|
|
Activité 2 : Par exemple « z » et « t » étant des
entiers naturels, considérons l’équations d’inconnues ( z ; t
) : « z – 2 t = 5 » dans l’ensemble des couples d’entiers
naturels. |
|
|
|
|
Remplacer « z » par « 17 » et « t » par « 6 » , vous obtenez …17 – 2 x 6 = 5 … , (vous calculez : 17 – 12 = 5 ) , vous
concluez que : l’égalité est ….vraie….. On dit alors que le couple de
nombres ( 17 ; 6 ) est « solution de l’équation ». |
|
|
|
|
|
|
|
|
|
Vocabulaire
(à
retenir) « résoudre une équation » ; c’est trouver les solutions
de cette équation ( et les trouver toutes). |
|
|
|
|
|
|
|
|
|
v Nous allons vous proposer un problème qui conduit à une équation dans
l’ensemble des couples d’entiers. |
|
|
|
|
|
|
|
|
|
Vous disposez de 1,50 € ( 150 centimes )et
vous voulez acheter des chewing-gums à
30 centimes et des caramels à
20 centimes. Combien des chewing-gums et de caramels pouvez-vous acheter
sachant que vous dépensez entièrement votre
argent ? |
|
|
|
|
|
|
|
|
|
Pour résoudre ce problème, il est commode de remplacer
les nombres cherchés par des lettres. « X » désignera le nombre de chewing–gums et
« y » désignera le nombre de caramels. |
|
|
|
|
|
|
|
|
|
-
La dépense pour les
chewing-gums (en centimes) est :
30 -
La dépense pour les
caramels ( en
centimes ) est ……… On peut poser
l’équation : L’équation ainsi
obtenue il reste à la résoudre …….à vous de jouer !!!!ce qui ne devrait être simple!! |
|
|
|
|
|
|
||||
|
|
Fiche 2 : Résolution de la forme « a +
x = b » |
Info @ sur la résolution de l’équation du premier
degré à une inconnue. |
|
|||
|
|
( il s’agit d’une
équation du premier degré à une inconnue : comportant une ’addition……) |
|
||||
|
|
|
|
||||
|
|
Exemple 1 :
Considérons l’équation « 2 + x = 7 » d’inconnue « x ». |
|
||||
|
|
« x » est le nombre qu’il faut ajouter
à « 2 » pour obtenir « 7 ». C’est dons la soustraction
de « 7 » et de « 2 » dans cet ordre . « 7 – 2 = x » « 2 + x = 7 » a même signification que « x = 7 –
2 » c'est-à-dire « x = 5 » Vérification : 2 +
…5 ….=
7 L’équation a pour solution unique le nombre …5……. |
|
||||
|
|
Exemple 2 : Considérons l’équation ( + 8 ) + y = ( -
5 ) d’inconnue « y ». « y » est le nombre qu’il faut ajouter
à ( + 8 )
pour obtenir ( - 5 ). D’après ce que nous avons vu ci-dessus :
c’est donc la différence de …….et de ……..pris dans cet ordre : ( - 5 ) – ( + 8 ) = ( -5 ) + ( - 8 ) =
( - 13) Ainsi : ( + 8 ) + y = ( - 5 ) a même
signification que « y = ( - 5 )
– ( + 8 ) » c'est-à-dire « y = ( - 13 ) » Vérification : ( + 8 ) + (
- 13 ) = ( - 5 ) . L’équation a pour solution unique de nombre ..( - 13 ) .. · D’une manière générale, « a » et « b » étant des nombres quelconques, « a + x = b » signifie que « x = b – a » Le calcul de « b – a » est toujours
possible et donne un résultat unique. On dira alors. |
|
||||
|
|
A retenir : L’équation ( de la forme ) « a + x = b » d’inconnue « x » , a pour
solution unique le nombre « b – a ». |
|
||||
|
|
|
|
||||
|
|
|
|||||
|
|
|
|
||||
|
|
Activité N° 1 |
|
||||
|
|
Résolvez les équations suivantes d’inconnues
respectives « z » , « t » ,
« u ». |
|
||||
|
|
« z + ( - 4 ) = (
- 7 ) » |
|
( - 3 ) |
|
||
|
( - 2 , 3 ) = ( + 7,5 ) + t |
|
( - 9, 8 ) |
||||
|
( + 4,2 ) + u + ( - 5 , 8 ) = ( + 5 ) + ( - 3,7 ) |
Regrouper les nombres
,dans chaque membre : u + (– 1,6) = ( + 1,3 ) |
( + 2,9 ) |
||||
|
|
|
|
||||
|
|
Activité N° 2 |
|
||||
|
|
Situation problème : A Paris , un jour
d’hiver, la température à 14 h était ( + 3 ) degré. Quelle était la température à 8 h sachant que de 8h à 14 h elle a
augmenté de 7° ? |
|
||||
|
|
Résolution : Appelons
« x » la température à 8 h . Traduisons l’énoncé : x + ( + 7 ) = (
+ 3 ) A vous de résoudre cette équation. |
|
||||
|
|
|
|
||||
|
|
Activité N° 3 |
|
||||
|
|
Situation problème : Un autre jour , à 20 h , la température était ( - 2 ) degré. Quelle
était la température à 13 h sachant que de 13 h à 20 h ,
elle à diminué de « 6° » ? |
|
||||
|
|
|
|
||||
|
|
v Autre forme d’équation : a – x = b |
|
||||
|
|
|
|
||||
|
|
Exemple : considérons l’équation ( + 7 ) – x = ( - 2
) d’inconnue « x ». |
|
||||
|
|
|
|
|
|||
|
|
( + 7 ) – x = (
- 2 ) signifie que ( + 7 )
= ( - 2 ) + x |
( + 7 ) – x + x
= ( - 2 ) + x (en ajoutant +x de chaque côté on ne
modifie pas l’égalité ) ; et – x + x = 0 , d’où après simplification ( +
7 ) = ( - 2 ) + x |
|
|||
|
|
Or : ( + 7 ) = ( - 2 ) + x
signifie que ( + 7 ) - ( - 2 ) =
+ x ; où x = (
+ 7 ) - ( - 2 ) ; soit x = ( + 7 ) + ( + 2 ) ; soit x = ( +9 ) |
|
||||
|
|
Vérification : ( + 7 ) - ( + 9 ) = ? = ( -
2 ) ; ce qui est vraie ( + 7 ) + ( - 9 ) = ( - 2 ) |
|
||||
|
|
|
|
||||
|
|
Activité : Résolvez les équations suivantes d’inconnues
respectives « y » et « z ». |
|
||||
|
|
( - 8,7 ) – y = ( - 2, 5 ) |
( - 8,7 ) – ( -
2, 5 ) = y |
|
|||
|
( - 3,4 ) = ( + 5,2 ) – z |
z = ( + 5,2 ) – ( - 3,4 ) |
|||||
|
|
|
|
||||
|
|
Remarque : Vous avez déjà résolu d’autres types d’équation ( sans en avoir prononcé le mot ) Par exemple , dans
l’ensemble des nombres positifs. |
|
||||
|
|
6 x = 18 ; x = …….3…….. |
|
|
|||
|
|
|
|
||||||
|
|
Fiche 3
Comparaison de nombres relatifs. |
|
||||||
|
|
|
|
||||||
|
|
Vous savez que l’on peut écrire par exemple ( + 3 )
= 3 ( mais attention
cette simplification peut vous poser des problèmes et engendre des erreurs ,
parce qu’il faut remarquer que l’on dira que
« 3 » est la @ valeur absolue des nombres
relatifs ( +3 ) et ( - 3 )..) Aussi
comparer des entiers relatifs positifs reviendra à comparer les
entiers naturels correspondants. Sachant que
5 < 7 , on pourra écrire que ( + 5 ) < ( + 7 ) |
|
||||||
|
|
Activité : Complétez la portion de droite graduée
représentant les entiers relatifs. |
|
||||||
|
|
|
|
||||||
|
|
Premier complément
avec les nombres en écriture simplifiée…. |
|
||||||
|
|
|
|
||||||
|
|
Graduation tel que cela devrait être. |
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
Sur la droite graduée , les
entiers positifs sont rangés dans l’ordre croissant. De la gauche vers la
droite. Il en est
ainsi pour l’ensemble des entiers relatifs. De deux
nombres relatifs représentés sur la droite graduée ,
le plus grand nombre est celui qui est le plus à droite ou encore , le plus
petit est celui qui est le plus à ………gauche
…………… |
|
||||||
|
|
Exemple : |
|
||||||
|
|
|
|
|
|||||
|
|
Sur la graduation : |
( + 7 ) est à droite de ( +3 ) |
On écrit ( +
3 ) < ( + 7) |
|
||||
|
|
« 0 » est à …gauche…..de ( + 4 ) |
On écrit ………< ………… |
||||||
|
|
( + 2 ) est à …droite
….de ( - 5 ) |
On écrit …( - 5) …< …( + 2 )… |
||||||
|
|
« 0 » est à ……de ( - 6 ) |
On écrit ………< ………… |
||||||
|
|
( - 7 ) est à …………….de ( -3 ) |
On écrit ………< ………… |
||||||
|
|
|
|
||||||
|
|
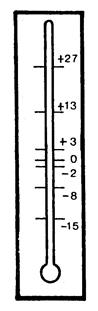
v On vous donne des informations que nous avons relevées sur la
graduation d’un thermomètre. « 21 »
degré au-dessus de zéro peut être représenté par ( + 21 ) « 15 » degré au-dessous de zéro peut
être représenté par ( -15) ( + 13 ) est plus froid que ( +27 ) , on
écrit ( + 13 ) < ( + 27 ) ( - 15 ) est ………………..que ( + 3 ) , On écrit ……………..< ……………….. ( - 8 ) est …………………que ( - 2 ) ,
on écrit ……………..< ……………….. |
|
|
|||||
|
|
|
|
||||||
|
|
v Ce que l’on vient de dire pour
les entiers est valable pour les nombres décimaux. |
|
||||||
|
|
Il suffit de prendre des subdivisions sur la graduation……….. |
|
||||||
|
|
|
|
||||||
|
|
Activité :
On vous demande de placer des valeurs. Placez sur la droite ( +3,4
) et ( + 0,7 ) . Vous pouvez écrire ( + 0 ,7) < ( + 3 , 4 ) Placez sur la droite ( +1
, 5 )
et ( - 2 , 3 ) . Vous pouvez écrire ( - 2,3 ) < ( + 1 , 5 ) Placez sur la droite ( -
3,6 )
et ( - 0,8 ) . Vous pouvez
écrire ( ………) < ( …………. ) |
|
||||||
|
|
Corrigé
|
|
||||||
|
|
|
|
||||||
|
|
Utilisation des symboles : |
|
||||||
|
|
|
3 < 7 |
7 > 3 |
|
|
|||
|
|
( + 3 ) < ( + 7 ) |
( + 7 ) > ( + 3 ) |
|
|||||
|
|
( - 5 , 33 )
< ( +
1, 27 ) |
( + 1, 27 )
> ( - 5 , 33 ) |
|
|||||
|
|
|
|
||||||
|
|
Activité n°…… |
|
||||||
|
|
Complétez en utilisant le symbole qui convient : |
|
||||||
|
|
( - 3 ) ………..( - 7 ) |
( - 4, 7 ) ……..( + 3,9 ) |
( + 0 , 7 ) …………..( - 9,34) |
( + 1,79) ……..( + 1,8 ) |
|
|||
|
|
|
|
||||||
|
|
v « a » et « b »
|
|
||||||
|
|
« |
|
||||||
|
|
« |
|
||||||
|
|
|
|
||||||
|
|
Activité n°…… |
|
||||||
|
|
Donnez la liste des entiers relatifs « x » tels que : |
|
||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
Fiche 4 : Nombres relatifs opposés. |
|
|
|
|
|
|
|
|
|
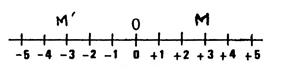
Activité n°.1. ; |
|
|
|
|
( + 3 ) et ( - 3 ) sont des
nombres relatifs ..Opposés…… Sur la droite graduée d’origine « O » , ci-contre , placez les points « M » et « M’ »
d’abscisses respectives ( + 3 ) et ( - 3 ). |
|
|
|
|
Vous constatez que « M’ » et « M »
sont opposés par rapport à « O ». |
|
|
|
|
|
|
|
|
|
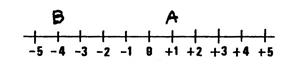
Activité n°.2. ; |
|
|
|
|
Sur
la droite ci-contre placez les points « A »
et « B » d’abscisses ( + 1 ) et ( -4). « A » est à la droite de « B » , on a alors
( + 1 ) …..( - 4 ) |
|
|
|
|
Placez les points « A’ » et « B’ »
dont les abscisses sont les opposés des abscisses de « A » et « B ». « A’ » est à ……gauche…. de « B’ » , on a alors ( - 1 ) …..( + 4 ) |
|
|
|
|
|
|
|
|
|
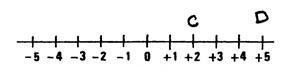
Activité n°.3. ; |
|
|
|
|
Sur la droite graduée ci-contre placez les points « C » et « D »
d’abscisses ( +
2 ) et ( + 5 ) ; « C » est à la …droite….de
« D ». Placez les points « C’ » et « D’ »
dont les abscisses sont les opposés
des abscisses de « C »
et « D » . |
|
|
|
|
« C’ » est à …droite ……….de
« D’ » , on a alors ( …..) …….( ….) |
|
|
|
|
Vous pouvez choisir d’autres exemples
, vous constaterez toujours que : |
|
|
|
|
|
|
|
|
|
A retenir : Si des nombres sont rangés dans un certain ordre ,
leurs opposés sont rangés dans l’ordre opposés. |
|
|
|
|
|
|
|
|
|
Activité n°….. |
|
|
|
|
Voici une liste de nombres relatifs : ( - 5 ) ; ( + 9 ) ; ( - 12 ) ;
( + 3 ) ; ( - 18 ) Rangez les nombres donnés dans l’ordre croissant :
…………………………………………………………………………………………. Ecrivez en
suite leurs opposés respectifs : ……………………………………………………………………………………………… Ils sont rangés dans l’ordre ………………………………………… |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Fiche 5 : Règle de comparaison des nombres
relatifs. |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Grâce à ce qui a été étudié dans la « fiche
3 » et la « fiche 4 » , on peut dire : |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
A retenir ….. -
Tout nombre positif
est supérieur ou égal à zéro. -
Tout nombre négatif
est …………inférieur ou égal ……………à zéro -
Tout nombre positif
est supérieur à tout nombre négatif.. -
De deux nombres négatifs , le plus grand est celui des deux dont l’opposé
est le plus ……………….. ou qui la valeur absolue la plus petite. |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Exemple : Comparons : ( - 7 ) et ( - 9
) : l’opposé (- 7) = (+ 7) et
l’opposé de ( - 9 ) = ( + 9 ) or (+
7) < ( + 9 )
donc ( - 7 ) > ( - 9) |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Remarque : « « |
|
|||||||||||
|
|
|
|
|||||||||||
|
|
Activité n °1. |
|
|||||||||||
|
|
( - 11 ) ……( +8 ) |
( + 9 ) ……( + 18 ) |
( - 11 ) ……..( - 23 ) |
( + 0,136) …..( + 0,23) |
|
||||||||
|
|
|
|
|
||||||||||
|
( 0 , 09 ) ………0 |
( - 13,7 ) ……….0 |
( + 0,007)………( - 239,4 ) |
( - 1,23) ……..( - 2,7 ) |
||||||||||
|
|
|
|
|
||||||||||
|
|
Activité n °2. |
|
|||||||||||
|
|
Rangez dans l’ordre croissant en utilisant le
symbole approprié. |
|
|||||||||||
|
|
( - 3,75 ) |
( + 2 ) |
( - 0,09) |
( - 3 ) |
( + 2,73) |
0 |
( + 0,011) |
( - 0,15) |
( - 7,7) |
( + 12,8) |
|
||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
16/2/2014 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CONTROLE : 1. Donner la définition de :
IDENTITE : 2. Donner la définition
de : EQUATION : 3. Donner la définition de :
Inconnues
4. Donner la définition de :
SOLUTIONS ou RACINES 5. Que signifie : EQUATION SATISFAITE ou VERIFIEE ? Aucune
évaluation. CORRIGE du CONTROLE. Donner la définition de : IDENTITE : On
appelle identité une égalité évidente ou une égalité satisfaite quelles que
soient les valeurs numériques des lettres qui y entrent. Donner la définition
de : EQUATION : On
appelle « équation » une égalité qui ne se réduit à une identité
que pour des valeurs particulières des lettres qui y entrent. Donner
la définition de : Inconnues
Les
lettres qu’il faut remplacer par des valeurs particulières pour obtenir une
identité sont les inconnues de l’équation ; on les désigne généralement
par les lettres « x » « y » « z »
« t » « u ». Donner la définition de : SOLUTIONS ou RACINES Les valeurs
particulières qu’il faut donner aux inconnues
pour avoir une identité sont appelées « les solutions » ou
« racines » de l’équation. Que signifie : EQUATION SATISFAITE ou
VERIFIEE ? On
dit qu’une équation est satisfaite ou vérifiée pour les valeurs des inconnues
qui sont racines. |
|
|
|
|
|
|
|
|
|
|
|
|
|