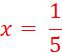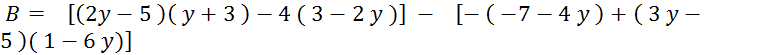Fiche 6  : Résolution d’équations.

Fiche 7 : Exercices types.

Fiche 8 : Situations problèmes.

Fiche 1 : Résolution d’équations

Activité 1 :

Résolvons l’équation  d’inconnue «  » .

Le premier membre de cette équation est un produit et ce produit doit être  ………. Or , vous avez vu dans le cours @ (calculs sur les nombres relatifs : fiche 6 )précédent  qu’un produit  est nul dans le seul cas où l’un des facteurs est   ..…..

Les solutions de l’équation sont donc les nombres qui sont solutions des équations :

C'est-à-dire :

L’équation a donc trois solutions :

Activité 2 :

Résolvez de même l’équation     d’inconnue   

Solutions :   0,7   et 

Activité 3 :

Résolvons l’équation    d’inconnue    .

Vous commencez par transposer :     

Puis vous factorisez : 

   c'est-à-dire    :   

Et vous résolvez cette équation comme précédemment : 

Solution :    et   

Méthode :

Pour résoudre de telles équations  , vous procédez de la manière suivante :

-        Vous transposez de telle sorte que le deuxième membre soit « 0 » .

-        Puis  vous factorisez et appliquez  le théorème : «  un produit de facteurs est nul, dans le seul cas où l’un des facteurs est nul ».

Activité 4 :

Résolvez l’équation :    d’inconnue «  »

Activité 5 :

Résolvez l’équation    d’ inconnue «  »

Activité 6 :

Résolvez l’équation    d’inconnue  «  » .

Vous commencez par transposer :  

Puis vous essayez de factorisez , mais vous ne trouvez pas de facteur commun.

Dans ces conditions, vous n’avez qu’un seul recours , développez et réduisez .

Remarque : n’utilisez ce procédé que si vous ne pouvez pas factoriser  ( voir fiche 3 )

Activité 6 :

Résolvez l’équation :     d’inconnue  «  »

Activité 7 :

Résolvez , sur un feuille à part, les équations suivantes d’inconnue « ».

Fiche 7 : Exercices

Activité 1 :   «  » et «  » désignant des nombres, développez, réduisez et ordonnez « » et « » .

« A » :           ; conseil : commencez par développer :

« B » :  

Activité 2 :    Factorisez  « C » ; « D » , « E »  ( à faire sur une copie )

Activité 4 :    (D’après le brevet de Créteil 87 ) . A faire sur une autre feuille .

1°) Développer , réduisez et ordonnez

2°) Factorisez :

3°)  Calculez : 

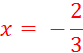
4°) Résolvez les équations   pour : 

Activité 5 :    A faire sur une autre feuille.

1°) Développer , réduisez et ordonnez

2°) Factorisez :

3°)  Calculez : 

4°) Résolvez les équations   pour : 

Fiche 8 : Situations problèmes.

Situation problème 1 :

Un rectangle a « 7 m » de long et « 5 m » de large .

On diminue la longueur de « x » mètres et on augmente la largeur de « x » mètres.

Déterminez « x » de telle sorte que l’aire du rectangle ne change pas .

Quelle remarque pouvez-vous faire ?

Situation problème 2 :

« ABC » est un triangle isocèle rectangle en « A ».

« AB= AC = 9 cm . « M »  est un point de  [ BC ] .

« M » se projette orthogonalement sur (AB) en « H » et sur ( AC ) en « K ».

1°) Démontrez que « AKMH » est un rectangle et « MKC » et un triangle isocèle.

2°) On désigne par « x » la longueur « AK ».

  Exprimez en fonction de « x » l’aire du rectangle  «  AKMH » et l’aire du triangle « MKC ».

3°) Pour quelle (s) valeur (s) de « x » , l’aire du rectangle «  AKMH » est –t-elle égale à l’aire du triangle « MKC » ?.

Situation problème 3 :

« ABC » est un triangle isocèle rectangle en « A ».

« AB=  7 cm ;   AC = 10 cm . »

Une parallèle à ( AB ) coupe [AC] en « E » et  [ BC]  en « F ». On désigne « EC » par « x ».

1°) Calculez « EF » en fonction de « x ».

2°) Calculez, en fonction de « x » , l’aire   du triangle  « EFC ».

3°) Calculez, en fonction de « x » , l’aire   du trapèze  « AEFB ».

4°) Pour quelle (s) valeur (s) de « x » , l’aire du trapèze  est –t-elle le triple de l’aire du triangle  ?.