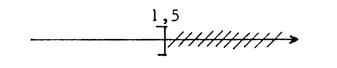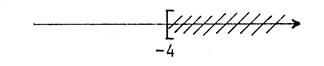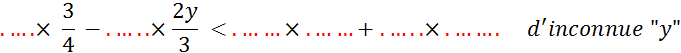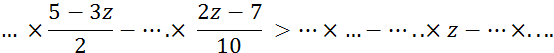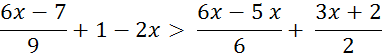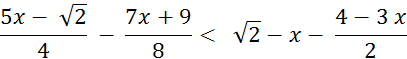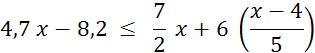Fiches de travail : premier degré « INEQUATIONS à une inconnue  » au collège 3^ème

Programme classe de 4^ème

Vers le corrigé

2°)   En appelant «  » le nombre de jours de location en un an :

Exprimez en fonction de «  » la dépense  ( en € ) avec la formule « A ».

Exprimez en fonction de «  » la dépense  ( en € ) avec la formule « B ».

3°) Pour quel nombre de location de voiture  la dépense est-elle la même pour les deux formules ?

Dans ces conditions , on doit avoir : 

Vous êtes en présence d’une équation du premier degré à une inconnue  ; A vous de la résoudre.

Réponse : La dépense est la même pour les 2 formules pour  …. … locations .

4°) Pour combien de locations la formule « B » est-elle plus avantageuse que la formule « A » ?

(Conseil : il faut chercher pour quelles valeurs de « x » la dépense avec la formule « A » est supérieure à la dépense avec la formule « B ».)

C'est-à-dire      ; Vous êtes en présence  d’une . ………………...

Tout nombre mis à la place de « x » pour lequel l’inégalité  correspondante est vraie est appelé « solution » de l’inéquation.

·       En utilisant le tableau de la première question , donnez des solutions : ……………………

·        Résolvez une inéquation c’est trouver toutes les solutions de cette inéquation.

·       A vous de résoudre cette inéquation (comme vous l’avais appris en classe de 4^ème )

              Réponse : La formule « B » est plus avantageuse  que la formule « A » dès que le nombre de jours loués est strictement supérieur à « 11 » .

5°) On dispose de  325 € , quelle  est la formule qui permet de louer la plus  grande nombre de jours . Justifiez votre réponse.

Résoudre : 

6°) La direction du magasin de location propose de remplacer la formule « B » par la formule « C » .

Fiche 2 : Résolution d’inéquations du premier degré à une inconnue.

Info :pré requis sur les transformations d’une égalité..

Exemple 1 : Résolvons l’inéquation «   » d’inconnue « ».

En imaginant que « u » représente une solution de l’inéquation, on est en présence d’une inégalité .

ON peut donc lui appliquer les règles de la leçon « …… » fiche 4 …..

Ajoutons « 8 » aux deux membres  , on obtient : «   »

Et après simplification , il reste : «   »

Ajoutons  « 5 u » aux membres  , on obtient :  «   »

Et après simplification , il reste : «   »

Remarque :

Vous constatez que tout revient à « transposer » « - 8 »  et « -5u » ( en changeant de signe ).

On a donc la même règle de transposition que pour les équations.

Ø Grâce à la règle de la leçon (fiche 5 )  , on peux diviser les deux membres par « 8 ».

     a les mêmes solutions que  «    c'est-à-dire  «   »

L’inéquation obtenue : «   » et l’inéquation  donnée ont les mêmes solutions.

Ce sont les nombres inférieurs ou égaux à  «  1,5 »

Représentation graphique des solutions :

Exemple 2 :

Résolvons  l’inéquation  «  » d’inconnue «  ».

Explique pourquoi (verbalement ) on ne change pas les solutions en développant.

On obtient :  «  »

En raisonnant comme à l’exemple précédent ( n°1) , on peut transposer  «  » ; «  » et «  »  ;

On obtient : «  » ;

«  » ;

«  » ;

« » ;

«  » ;

« » ;

« »

Ø Grâce à la règle de la leçon (fiche 5 ) , on peut diviser les deux membres par « -5 » .

Mais attention ! « -5 » est négatif , on obtient alors une inégalité de sens .. . ……. … »

«   » a les mêmes solutions que «   »  , c'est-à-dire «   »

Les solutions de l’inéquation donnée  sont les nombres strictement inférieurs  à  «  »

Représentation graphique des solutions :

Exemple 3 :

Résolvons l’inéquation : «   »  d’inconnue « y » .

Multiplions les deux membres par le dénominateur commun le plus petit possible : « . ….. »

Info @ sur le PPDM

Et développons , on obtient :

On multiplie tous les termes par « 12 »   :

Et après simplification , on obtient :         

A vous de terminer :

Représentation graphique :

A faire ……………….

Méthode de résolution des inéquations du premier degré à une inconnue :  

Info @ sur ++++

Pour résoudre une inéquation du premier degré à une inconnue , on écrit une succession d’inéquations ayant les mêmes solutions jusqu’ à ce que l’on trouve une inéquation de la forme :  x > k     (ou   ) .

Dans la pratique , on utilise les règles c- dessous qu’il est possible de démontrer en utilisant les propriétés ( de la leçon @@ )

Règles :

Etant donné une inéquation , on obtient une inéquation ayant les mêmes solutions  en :

-        En transformant l’écriture de chaque membre individuellement .

-        En ajoutant ou retranchant un même nombre (ou terme) aux deux membres.

( ce qui revient à transposer un terme en changeant de signe )

-        En multipliant ou en divisant les deux membres par un nombre strictement positif.

-        En multipliant ou en divisant les deux membres par un nombre strictement négatif  , sans oublier de changer le sens de l’inéquation.

Fiche 3 : Exercices de résolution d’inéquations.

Info ++ sur d’autres exercices ou situations problèmes .

Exercice 1 :

Résolvez l’inéquation : 

Faire dans l’ordre :

-        Développez :

-        Transposez :

-        Réduisez les termes semblables

-        Divisez les deux membres par :

-        Donnez la représentation graphique des solutions :

Exercice 2 :

Résolvez l’inéquation         

Multipliez les deux membres par le dénominateur commun qui est : .   ………

Et développez :

Simplifiez :

Développez :

Transposez :

Réduisez les termes semblables

Divisez les deux membres par :

Donnez la représentation graphique des solutions :

Exercice 3 :

Résolvez l’inéquation suivante d’inconnue « x » ( à faire au brouillon )

Ecrivez les solutions , et faites la représentation graphique des solutions.

Exercice 4 :

Résolvez l’inéquation suivante d’inconnue « x » ( à faire au brouillon )

Ecrivez les solutions , et faites la représentation graphique des solutions.

Exercice 5 :

Résolvez l’inéquation suivante d’inconnue « x » ( à faire au brouillon )

Ecrivez les solutions , et faites la représentation graphique des solutions.

Fiche 4 : Cas particuliers.

Exemple1 :  Résolvez l’inéquation : 

Développez :

Transposez :

Réduisez les termes semblables :

Quel que soit  le nombre «  » ,  L’inégalité   est vraie .

Tous les nombres sont donc solutions de l’inéquation.

Exemple  2 :  Résolvez l’inéquation : 

Développez :

Transposez :

Réduisez les termes semblables :

Quel que soit  le nombre «  » ,  L’inégalité   est . …….. .

L’inéquation . ……………………………………………………………………………..

Activités :

Donnez les solutions des inéquations d’inconnue «  » ci-dessous.

Fin le 11 / 10 /2015

Suite voir : Les systèmes d’inéquations à une inconnue.

Exercices

solution

1-

2x < 23,4

2-

-1,5 "e 69

3-

3 ( x + 1 ) "e x - 2

4-

> 4

Résoudre :

Résolution

1-a

 5x – 7  <   1

1-b

-2x + 2 < 5,7

1-c

8 ( 6x + 3) > 2x

1-d