Auteur : WARME R.

TRAVAUX ETUDE 2 du cours.

Rechercher dans le cours les informations.

Vers la leçon	Préparation :
N°8 Vers le corrigé	LES TABLEAUX NUMERIQUES, le REPERAGE sur une droite et dans un plan .

ETUDE 2 DU COURS

i9

I. LE TABLEAU NUMERIQUE

:i

ETUDE 2 /2 . « tableau » 

Identifier les tableaux : sont -ils à simple ou double entrées ?

Tableau 1 : :

Nom des classes : ( secteurs)	Effectifs
Pré - professionnelle	18
En 6^ème	65
En 5^ème	74
En 4^ème	59
En 3^ème	58

Combien y a t- il de collégiens en 5^ème ? .

Tableau 2  :

Dans le collège , les élèves garçons et filles se répartissent de la façon suivante . :

	Filles	Garçons	Total
Classe pré professionnelle	6	12	18
6^ème	36	29	65
5^ème	39	35	74
4^ème	35	24	59
3^ème	30	28	58

Exploitation du tableau 2 :

A quelle catégorie appartient l’effectif « 36 » ?

A quelle catégorie appartient l’effectif « 12  » ? .

A quelle catégorie appartient l’effectif « 28 » ? .

Tableau 3 :

Corps pur	Fer	Cuivre	Argent	Zinc	Plomb	Etain	Eau	Alcool
Température de fusion ( °C)	1535	1083	960	420	327	232	0	- 139
Température d’ébullition ( °C°)	2750	2336	2000	907	1740	2270	100	79

Quelle la température de fusion du zinc ? …………………………….. ;

Quelle est la température d’ébullition du cuivre ? ……………………..

Dans la liste proposée quel est le corps pur qui a la plus petite température de fusion ?........ .....

Dans la liste proposée quel est le corps pur qui a la plus grande température d ‘ébullition ?...... .......

Tableau 4  :

Nom des classes . (secteurs)	Pré - professionnelle	En 6^ème	En 5^ème	En 4^ème	En 3^ème
Effectifs	18	65	74	59	58

Combien y a t- il de collégiens en 4 ^ème ?

Tableau 5

Vitesse en Km/h	20	40	60	80	100	120
Distance (m)	20	40	80	140	220	320

Q : Traduire ce qui peut être lu dans la 5^ème colonne :

Tableau 6

Un libraire solde des cahiers en les vendant par lots de « 3 ».Un lot de « 3 » cahiers est vendu 5 €.

Compléter le tableau .

Nombre de lots	1	4		7	10
Prix ( en €)	5	20	30	35

i9

II. REPERAGE sur un axe

Cd : Info plus !  !

ETUDE 2 /2 « axe »

a) Déterminer la longueur unité "u" ; placer le point origine ; donner les abscisses entières comprises entre les deux points représentés.

Activité n°8  : Déterminer la longueur unité "u" ; placer le point origine ; donner les abscisses entières comprises entre les deux points représentés.

A)

B)

i9

III. REPERAGE DANS UN PLAN.

Cd :Info N°1plus !  ;Cd : Info N°2 plus !

ETUDE 2 « plan »

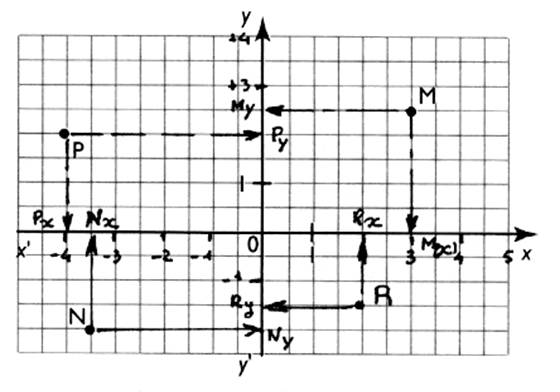
On place dans un repère cartésien des points : ( M , P , N, R )

On en déduit les informations suivantes :

Compléter le tableau ci dessous :

	Abscisse	Ordonnée	Coordonnées	Nota
M
P
N
R

i
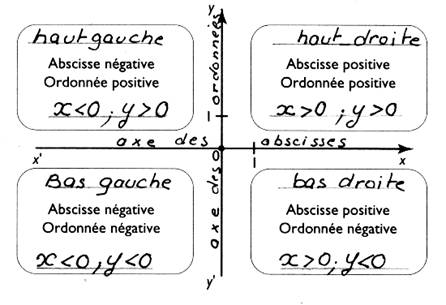
Zones	Points	Tracer un repère cartésien possédant les 4 zones  et placer les points dans la zone correspondante
x <0 ; y > 0	R
x>0 ; y < 0	S
x > 0 ; y > 0	T
x<0 ; y < 0	V

3 - Abscisse du milieu d’un segment sur un axe

Info plus .

ETUDE 2 «milieu d’un segment »

Devoir 2 / 2 : soit la formule ci dessous .

Que permet - elle ? Faire un schéma représentant ces abscisses.

xM =

Exercice : Sur une droite graduée "x"; on trace un segment AB tel que A = + 5 ; et B = (+8) ; quelle est la position du point M ( milieu) sur la droite graduée ?

Info 1 plus : des modèles de tracés! ! !

IV. Repérage : représentation graphique d’une FONCTION.

:i ; Info 2 :  « définition d’équation »

ETUDE 2 « représentation d’une fonction  »

+Activité n°9 : Représenter une fonction dans un repère.

Cd :Info plus !!sur « tracer uns courbe !!!

Définition :

La représentation graphique d’une fonction f dans un repère est constitué par tous les points dont les coordonnées sont ( x ; y )  ou , puisque y = f(x) ; ( x ; f(x))

Exemples :

1°) On veut représenter graphiquement la fonction dont l’équation est  f₁ (x) = 2,5 x pour des valeurs de x comprises entre 0 et 4.

On demande de remplir le tableau suivant : ( il faut calculer pour chaque point sa valeur « y »)

	A1	A2	A3	A4	A5	A6	A7	A8	A9
x	0	0,5	1	1,5	2	2,5	3	3,5	4
f1(x) ( = y)

On donne le papier millimétré suivant : on demande de placer les points « A….., » après avoir calculer pour chacun ses coordonnées

ETUDE 2 « repérage dans un plan  »

Exercice 1 : Compléter le tableau suivant: avec l’équation : f₂(x) = x - 1

	B1	B2	B3	B4	B5	B6	B7	B8	B9
x	0	0,2	0,5	0,8	1	2	3	4	5
f2(x) = y

et placer les points B_n dans un repère cartésien .

3° Exercice  : soit l’équation f₃(x) = -2x + 0,5 , Compléter le tableau suivant:

Identifier les points avec une lettre et placer ces points dans un repère cartésien.

x	0	-0,2	-0,5	-0,8	-1	-2	-3	-4	-5
f3(x)

4°) Compléter le tableau pour f ₄(x) = - 0,5 x

Identifier les points avec une lettre et placer ces points dans un repère cartésien.

x	0	-0,2	-0,5	-0,8	-1	-2	-3	-4	-5
f 4(x)

5°) Tracer la fonction y = x² :

On donne  : f₁ = y₁ ; telle que f₁(x) = x²

Compléter par calcul les tableaux 1 et 2 ci dessous .

Tableau 1 : le calcul repose sur des nombres négatifs

x	0	-0,2	-0,5	-0,8	-1	-2	-3	-4	-5
x^2 = y1

Tableau 2 : le calcul repose sur des nombres positifs.

x	0	0,2	0,5	0,8	1	2	3	4	5
x^2 = y 1

A) Faire la représentation graphique  de la fonction y = x ² ; base choisie  est : ( i = 1cm ; j = 0,5 cm)

B) Faire la représentation graphique  de la fonction y = x ² ; pour « x » compris -1 £ x £ + l ; base choisie est ( i = 5cm ; j = 5 cm )

Nous avons obtenu la même allure de la courbe !!!

FIN DES TRAVAUX AUTO FORMATIFS destinés à étudier le cours.