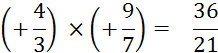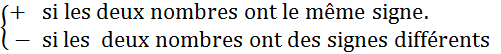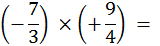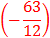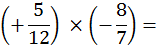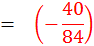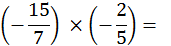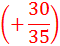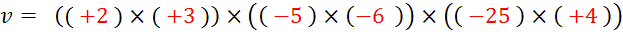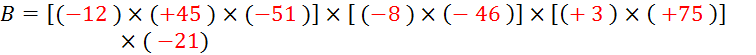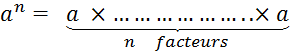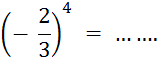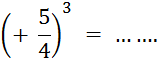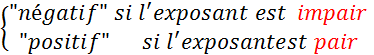|
|
Classe de
4ème |
||
|
|
|
|
|
|
|
|
||
Définition
de lobjectif : savoir faire la multiplication de deux nombres relatifs.
Rappel
:
I ) Objectif N°1 « la valeur
absolue »
II ) Se souvenir qu à
chaque fois que lon fait un calcul avec deux nombres relatifs , le résultat
est un troisième nombre relatif ; dont on devra rechercher : sa valeur absolue
et son signe.
III) Multiplication :
Le
produit « ab » est égal à la somme du nombre « b » , «
a » fois .
« a » et « b » sont appelés « facteurs »
Le «
produit » est le résultat dune multiplication.(de
deux nombres )
On ne «
traite » que deux nombres à la fois. On ne peut pas calculer directement deux
opérations en même temps.
IV)
Pour comprendre ce quest un nombre relatif se souvenir qu
un nombre négatif : représente de « largent dû » (une dette ; de largent en
« moins » ) et quun nombre positif représente une «
rentrée dargent ». (de largent en « plus »)
Pré requis :
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : 5. Addition de nombres relatifs 6. Leçon précédent 4ème
. |
Objectif suivant |
DOSSIER: Liste des fiches de travail
|
|
Fiche 1 :
Règle des signes pour un produit de deux nombres relatifs. |
|
|
|
Fiche 2 :
ACTIVITES |
|
|
|
Fiche 3 :
Les propriétés de la multiplication des nombres relatifs. |
|
|
|
Fiche 4 :
Produit de plusieurs nombres relatifs. |
|
|
|
Fiche 5 :
Règles des signes pour un produit de plusieurs nombres relatifs. |
|
|
|
Fiche 6 :
Puissances de nombres relatifs. |
|
|
|
|
|
|
|
Corrigé Contrôle DRMultipl cor.htm - cont |
Corrigé évaluation DRMultipl cor.htm |
FICHES
.
|
|
Fiche 1 : Règle des signes pour
un produit de deux nombres relatifs. |
|
|||||||
|
|
La
multiplication des nombres relatifs est une opération qui « prolonge » la
multiplication des nombres
décimaux « sans signe » et qui a les mêmes propriétés. Le
signe du produit de deux nombres relatifs dépend du signe de ces nombres. ( dans ce qui suit nous allons voir les 4 cas.) |
|
|||||||
|
|
A ) Produit dun positif par un positif. |
Exemple : |
|
|
|||||
|
|
Puisque
( + 4 ) sécrit « 4 » et ( + 3 ) sécrit « 3 »
; alors |
|
|||||||
|
|
Et comme 4 |
( + 4
) |
|
||||||
|
|
Il
en est de même pour tous les nombres relatifs positifs. |
|
|||||||
|
|
( + 0,
3 ) |
|
|
||||||
|
|
On
dira alors : le produit dun nombre
positif par un nombre positif est un nombre positif. |
|
|||||||
|
|
|
|
|||||||
|
|
B ) Produit dun positif par un négatif. |
Exemple : ( + 4 ) |
|
|
|||||
|
|
|
|
|||||||
|
|
De
même ( |
|
|||||||
|
|
|
|
|||||||
|
|
Donc |
|
|
||||||
|
|
|
|
|||||||
|
|
IL
en est toujours ainsi avec des nombres entiers. Vous admettrez quil est de même pour tous
nombres relatifs. |
|
|||||||
|
|
( +
2,5 ) |
|
|
||||||
|
|
On
dira alors : le produit dun nombre
positif par un nombre négatif est un nombre négatif. |
|
|||||||
|
|
|
|
|||||||
|
|
C ) Produit dun négatif par un positif. |
Exemple
: |
|
||||||
|
|
|
|
|||||||
|
|
La
multiplication des nombres relatifs doit être commutative. On doit donc avoir |
|
|||||||
|
|
Et comme |
|
|
||||||
|
|
Vous admettrez quil est de même pour tous
nombres relatifs. |
|
|||||||
|
|
|
|
|
||||||
|
|
On dira alors : le produit dun nombre négatif
par un nombre positif est un nombre négatif. |
|
|||||||
|
|
|
|
|||||||
|
|
D ) Produit dun négatif par un négatif. |
Exemple
: |
Info
Multiplication.htm |
|
|||||
|
|
|
|
|||||||
|
|
Vous
avez pu constater que : Multiplier par un positif ne fait pas changer le
signe du produit. Multiplier par un négatif fait changer le signe. |
|
|||||||
|
|
Vous
concevez alors que si lon multiplie un négatif par un négatifs le résultat soit ..positif
|
|
|
||||||
|
|
|
|
|||||||
|
|
Vous
admettrez quil en est de même pour tous nombres négatifs. |
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|
||||||
|
|
On dira alors : le produit dun nombre négatif
par un nombre négatif est un nombre positif. |
|
|||||||
|
|
|
|
|||||||
|
|
Règle
: Pour faire le produit de deux nombres relatifs ,on
multiplie ces nombres sans tenir compte des signes. Puis
on attribue le signe |
|
|||||||
|
|
|
|
|||||||
|
|
Nota
: ce cours est une approche sur les calculs avec des relatifs
, il faudra approfondir ce travail en allant travailler les cours
proposés dans la liste suivante : SOMMAIRE sur les
nombres relatifs. |
|
|||||||
|
|
|
|
||||||||||||||||||||
|
|
Fiche 2 : ACTIVITES |
|
||||||||||||||||||||
|
|
Nota
: Sue
les écritures équivalentes : ( + 12 ) Lecture
: Lecture
: |
|
||||||||||||||||||||
|
|
Série
1 : Calculez : |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
( + 2,5 ) ( -
0,8 ) = |
( + 2,5 ) ( - 0,8 ) =( - 20 ) |
( - 0,03) ( +
0,6 ) = |
( - 0,03) ( + 0,6 ) = ( - 0,018 ) |
( - 7,2 ) ( -
0,1 ) = |
( - 7,2 ) ( - 0,1 ) = ( + 7,2 ) |
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
Série 2 : |
|
||||||||||||||||||||
|
|
Complétez la table de multiplication c- dessous. Cest une portion de la table de multiplication
des nombres entiers relatifs. Vous pourrez faire certaines remarques
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
4 |
4 |
4 |
|
|
4² = 16 |
|
|
|
|
||||||
|
|
(-12) |
(-3) (+3) = (-9) |
(-6) |
( - 3 ) |
0 |
3 |
3 |
3 |
6 |
3² = 9 |
12 |
15 |
18 |
|
||||||||
|
|
-8 |
-6 |
(-2)(+2) = (-4) |
|
0 |
2 |
2 |
2 |
2² = 4 |
6 |
8 |
10 |
12 |
|
||||||||
|
|
-4 |
-3 |
-2 |
(-1)(+1) = -1² =-1 |
0 |
1 |
1 |
|
2 |
3 |
4 |
5 |
6 |
|
||||||||
|
|
-4 |
-3 |
-2 |
-1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
||||||||
|
|
- 4 |
- 3 |
- 2 |
- 1 |
0 |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
||||||||
|
|
-4 |
-3 |
-2 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
||||||||
|
|
+4 |
+3 |
+2 |
-1 |
-1 |
-1 |
-1 |
-1 1² = -1 |
- 2 |
-3 |
-4 |
-5 |
-6 |
|
||||||||
|
|
+8 |
+6 |
+4 |
+2 |
0 |
-2 |
0 |
-2 |
-4 |
-6 |
- 8 |
- 10 |
- 12 |
|
||||||||
|
|
+12 |
+9 |
+6 |
+3 |
0 |
-3 |
0 |
-3 |
-6 |
-9 |
-12 |
-15 |
-18 |
|
||||||||
|
|
+16 |
+12 |
+8 |
+4 |
0 |
-4 |
0 |
-4 |
-8 |
-12 |
-16 |
-20 |
-24 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|||||||||||||||||
|
|
Fiche 3 : Les propriétés de la
multiplication des nombres relatifs. |
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
Les
propriétés de la multiplication des nombres relatifs découlent des propriétés
des nombres sans signe. Passons- les en revue : |
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
La Commutativité : |
|
|||||||||||||||||
|
|
( + 7
) |
( - 3 ) |
On a alors |
|
|||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
La
multiplication des nombres relatifs est commutative , signifie que : « |
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
Lassociativité : |
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
On convient
alors de ne pas mettre les parenthèses et on écrit : |
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
De
même La
multiplication des nombres relatifs est associative , signifie que : « a » ; « b »
; « c »
étant des nombres relatifs , |
|
|||||||||||||||||
|
|
LElément neutre
. |
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
( + 1 ) est élément
neutre pour la multiplication des nombres relatifs, signifie que : « a » étant un nombre quelconque , |
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
Inverse : |
|
|||||||||||||||||
|
|
Vous savez que : |
|
|
|
|||||||||||||||
|
|
Tout
nombre relatif non nul possède un inverse
( et un seul ) |
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
« |
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
Produit par (
- 1 ) : |
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
Multiplier
un nombre par ( + 1 ) revient à ne rien changer. Multiplier
un nombre par ( - 1 ) revient à changer le signe du nombre. Le
produit dun nombre relatif par ( - 1 ) est égal à lopposé de ce nombre. |
|
|||||||||||||||||
|
|
« |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
Fiche 4 : Produit de plusieurs
nombres relatifs. |
Info ++ chaine dopérations produit. |
|
|
|
« |
|
|
|
|
En principe , on ne sait pas calculer : Mais
Activité
: Calculer : |
|
|
|
|
Pour
vous amuser , imaginez dautres façons de placer les
parenthèses , puis effectuez le calcul. :
Autre façon : |
|
|
|
|
Remarque : Dans
la pratique , on peut faire le calcul en imaginant
parenthèses et crochets, comme on la fait au début, ce qui revient à
multiplier le premier facteur par le second , le résultat par le troisième ,
et ainsi de suite jusquau dernier. |
|
|
|
|
|
|
|
|
|
Activité
: calculez avec cette méthode :
|
|
|
|
|
Idem
:
|
|
|
|
|
|
|
|
|
|
· Il
est possible dutiliser à la fois lassociativité et la commutativité. Exemple
: Pour
se faire vous regroupez les facteurs de manière à pouvoir faire les calculs mentalement .
|
|
|
|
|
|
|
||
|
|
Fiche 5 : Règles des signes
pour un produit de plusieurs nombres relatifs. |
|
|
|
|
|
|
|
||
|
|
Rappels
: 1°)
Si dans un produit les facteurs sont positifs , le
produit est positif. 2°)Le produit de deux nombres négatifs est un nombre positif. 3°)
Le produit dun nombre négatif par un positif est un nombre négatif . Considérons
le produit : Grâce à la commutativité et à lassociativité , on peut regrouper les facteurs comme on
veut. Groupons
entre eux les facteurs positifs et groupons par « 2 » les facteurs négatifs.
|
|
||
|
|
En
utilisant les rappels précédents, vous pouvez dire que le contenu de chacun
des crochets est un nombre positif. Donc le produit est positif. |
|
||
|
|
·
Faîtes de même pour « B » :
Le
contenu de chaque crochet est un nombre positif . Le
produit de ces nombres est donc un nombre positif . Mais il reste un facteur négatif
, donc le produit sera négatif . |
|
||
|
|
En définitive : Si
on peut grouper les facteurs négatifs deux par deux sans quil en reste un
tout seul, alors le produit est positif
. ,
Dans ce cas , le nombre de facteurs négatifs est un
nombre « pair ». Si
après avoir groupé les facteurs négatifs deux par deux il en reste un , alors le produit est négatif
. Dans
ce cas , le nombre de facteurs négatifs est un
nombre « impair » . |
|
||
|
|
|
|
||
|
|
A retenir : Le
produit de plusieurs relatifs est un nombre relatif : · « Positif »
sil y a un nombre pair de facteurs négatifs. · ·
« Négatif » sil y a un
nombre impair de facteurs négatifs. |
|
||
|
|
|
|
||
|
|
Activité 1 :
Donnez le signe du produit des opérations suivantes : |
|
||
|
|
|
Quel
est le signe de D. :négatif. |
|
|
|
|
|
Quel
est le signe de E : négatif |
|
|
|
|
|
Quel
est le signe de F : positif |
|
|
|
|
Activité 2 :
Déterminez le signe des nombres non nuls « «
|
|
||
|
|
|
|
||
|
|
|
|
||||||||||||||||
|
|
Fiche 6 : Puissances de nombres
relatifs. |
|
||||||||||||||||
|
|
( - 3 ) 5 signifie : ( - 3 ) 5 se lit « ( - 3 ) exposant « 5 » et ( - 3 ) 5 est une puissance de ( - 3 ) ; « 5
» sappelle
.exposant. , il indique le nombre de facteurs égaux à ( -
3 ) Activité : Complétez
: |
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
A retenir : «
|
Par convention : « a 1 = a » Si a |
|
|||||||||||||||
|
|
|
|
||||||||||||||||
|
|
Activité 1 : Calculez
: |
|
||||||||||||||||
|
|
( - 2 ) 5 =
.. |
( - 0 , 3 ) 4 =
|
( 0 , 07 ) 3 =
.. |
|
|
|||||||||||||
|
( + 5
, 27 ) 1 = ( + 5,27) |
( - 43
, 7 ) 0 = 1 |
|
|
|||||||||||||||
|
|
Signe dune puissance. |
|
||||||||||||||||
|
|
· ( +
2 ) 5 = ( + 2 ) Cest le produit de nombres positifs donc ( + 2 ) 5 est un nombre positif . · ( -
2 ) 5 = ( - 2 ) Cest le produit dun nombre impair de négatifs
donc ( - 2 ) 5 est un nombre négatif . · ( -
2 ) 4 = ( - 2 ) Cest le produit dun nombre pair de négatifs
donc ( - 2 ) 4 est un nombre positif . |
|
||||||||||||||||
|
|
A retenir : Toute
puissance dun nombre positif est un nombre positif . Toute
puissance dun nombre négatif est un nombre : |
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
· Des deux
phrases suivantes, lune est fausse, barrez la ; lautre est vraie entourez la. |
|
||||||||||||||||
|
|
Affirmation A : Un carré peut- être négatif ou positif. ( fausse) |
Affirmation B : Un carré est toujours positif. ( vraie ) |
|
|||||||||||||||
|
|
|
|
||||||||||||||||
|
|
Activité 2 : Déterminez , si possible, les nombres qui ont pour carré ( + 49
) = ( + 7
)² ou ( - 7 )² |
|
||||||||||||||||
|
|
( +
0,04 ) est le carré de 0,2 |
; |
( - 16
) nest pas un carré |
|
||||||||||||||
|
|
|
|
||||||||||||||||
|
|
Activité 3 : Calculez
:
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
Opérations sur les puissances. |
|
||||||||||||||||
|
|
Les formules sont les mêmes que pour les nombres
sans signe . ( info ++@ cours
sur ) |
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
Activité 4 : Calculez
« B » : |
|
||||||||||||||||
|
|
B =
.. ; B =
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
Activité 5 :
Complétez le tableau ci-dessous. |
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
« a
» |
2a |
a² |
2
a² |
( 2a)² |
3a |
3
a² |
( 3 a
) ² |
a3 |
|
|
||||||
|
|
-2 |
-4 |
+4 |
-8 |
+ 16 |
-6 |
+ 12 |
+36 |
-8 |
|
||||||||
|
|
+ 5 |
10 |
+ 25 |
+ 50 |
100 |
+ 15 |
+ 30 |
225 |
125 |
|
||||||||
|
|
-5 |
- 10 |
+ 25 |
+ 50 |
100 |
-15 |
-30 |
-225 |
-125 |
|
||||||||
|
|
-10 |
- 20 |
+ 100 |
+ 200 |
+ 400 |
-30 |
-60 |
900 |
-1 000 |
|
||||||||
|
|
Ceci termine les fiches sur le produit
|
|
||||||||||||||||
|
|
TRAVAUX
AUTO FORMATIFS. |
|
|||
|
|
1.Que cherche -t-on à obtenir lorsque lon effectue la
multiplication de deux nombres relatifs? 2.Citer la règle concernant la multiplication de deux
nombres positifs? 3.Citer la règle concernant la multiplication de deux
nombres négatifs. 4
Citer la règle concernant la multiplication de deux nombres relatifs de signe
contraire (opposé) ..................(dans ce cas un
nombre est de signe + et un nombre est de signe -) 5.Transcrire en langage mathématique les règles précédentes. |
|
|||
|
|
|
|
|||
|
|
EVALUATION: Partie
I: |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
Partie II . Trouver le signe de « (rendre compte :pour
chaque «
Partie III: faire les opérations suivantes:
Partie IV: Calculer : |
|||||
|
Résoudre : |
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
( |
|
|
|||
|
|
|
|
|||
|
|
|||||