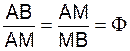|
2003 - 2004 - Mathématiques :
découverte du nombre d’or et calculs
appliqués
|
||
|
@ travaux auto - formatifs :niveau
V ; CAP BEP …. Doc. Warmé
.LP ameublement. |
|
|
« Il y a de la petite partie à la grande le même rapport que de la
grande au tout » commente
l’architecte romain Vitruve en parlant
du partage asymétrique des longueurs d’une figure dont le rapport de
dimension est établi selon le « nombre d’or ».
SOMMAIRE
|
Partie 1 |
Le NOMBRE D’OR (1/2) |
1 / 2 |
|
|
ٱ |
- Définitions des
MOTS : « divine proportion » ; « le rectangle
d’or » , « format « marine » des
peintres ».
|
|
ٱ |
A) Recherche du nombre d’or à
partir de la définition
B ) Recherche du
nombre d’or par le calcul :
|
|
ٱ |
|
(@) |
A) Partage d’un segment dans la divine
proportion: |
ٱ |
|
|
B) Construction
d’un rectangle à partir des segments |
ٱ |
-
a)
Par le calcul
-
b) Par le tracé.
|
|
C
) Construction d’un
rectangle à partir d’un carré. |
ٱ |
|
ٱ |
-
a) Pour réduire ;
-
b ) pour
agrandir.
|
|
ٱ |
-
Construction au compas
|
PARTIE 2 |
LE NOMBRE D’OR ( 2 / 2 ) |
2/2 |
A ) Compas de proportion de Galilée
B ) LA
DIVISION en « MOYENNE » ET
« EXTREME » RAISON.
SUITE : Pour
donner un prolongement et assurer un travail en interdisciplinarité, en Art
appliqué, on devra traiter de la
« composition selon le nombre d’or ».
|
Le symbole @ signifie qu’ il existe
un lien |
|
« Il y a de la petite partie à la grande le même rapport que de la
grande au tout » commente
l’architecte romain Vitruve en parlant
du partage asymétrique des longueurs d’une figure dont le rapport de
dimension est établi selon le « nombre d’or ».
|
|
ٱ |
Découvert d’une façon
empirique, dans l’architecture et dans la peinture, ce sont les Grecs avec
Pythagore ( v. 570-V 480 av. J.- C) qui ont attribué
au nombre d’or ses propriétés mathématiques.
L’usage de la
division au nombre d’or se répand dès le traité d’ Euclide
( III e siècle av.
J.-C.) qui indique son tracé au compas.
Le nombre d’or est
notamment lié (@) au pentagone régulier ainsi qu’à
divers autres (@) polygones et (@) polyèdres.
Empreint de mystère,
objet de culte tantôt religieux , tantôt magique , le
nombre d’or influence la vision occidentale de l’harmonie. Chez les Grecs , avec le développement de la géométrie , la secte
secrète des pythagoriciens en avait fait un symbole d’ harmonie universelle ,
de vie , d’amour et de beauté. A la renaissance , architectes , peintres et sculpteurs
cherchant à renouer avec l’ idéal
antique se sont réclamés de la doctrine platoniciennes des corps cosmiques ,
les cinq polyèdres réguliers , et on fait du nombre d’or , « la divine
proportion », un modèle de perfection esthétique et philosophique.
Le nombre d’or
correspond à une proportion particulièrement esthétique appelée « divine proportion » ;
il tient toujours une place importante dans le monde des arts et de
l’architecture.
C’est le rectangle
d’or , par
sa forme simple, qui permet d’approcher et de comprendre une construction
établie selon la « divine proportion ».
Il correspond à la
dimension du format « marine » des peintres. (
@ Info +)
|
Aujourd’hui ;,
d’autre nombres ((@) |
|
||
|
|
|
||
A)
Recherche du nombre d’or à partir de la définition :
1° Définition :
Le nombre d’or correspond à un rapport de
grandeurs, entre elles et par rapport au tout.
C’est le partage
d’une longueur en deux parties inégales, dans lequel le rapport de la grande
partie au tout est égal au rapport de la plus grande partie à la plus petite.
|
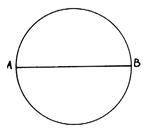
Soit le segment de
droite AB et un point M, situé sur ce segment, permettant d’obtenir la
relation suivante : |
|
Les fractions ![]() ou
ou ![]() approchent ce
rapport.
approchent ce
rapport.
Activité :
niveau IV (Bac. Prof) - Recherche du nombre d’or par le
calcul : A partir de la Construction de la divine proportion :
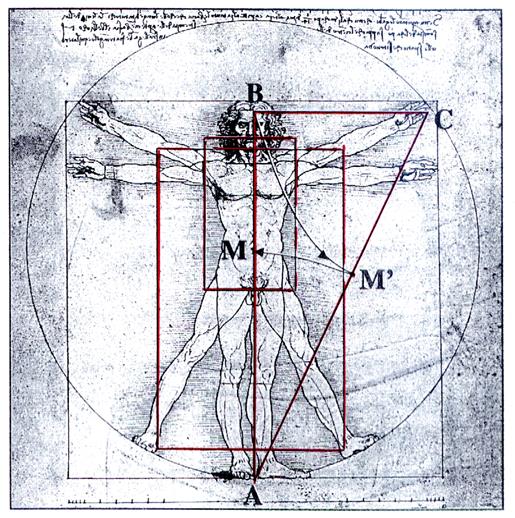
|
La distance AB
entre les pieds et la tête de l’homme présentant les mensurations idéales et
dessiné par Léonard de Vinci, est partagée par le nombril « M »
dans une proportion correspondant au nombre d’or. La construction de
la « divine proportion » prend appui sur le triangle rectangle
ABC rectangle en « B » tel
que : BC = Sur le dessin ci-contre , sont représentés des rectangles dont le rapport
entre la longueur et la largeur est égal au nombre d’or ; de tels
rectangles sont appelés « rectangles
d’or » |
|
Tracer un rectangle
semblable à celui de la figure, puis, en utilisant le principe de construction
indiqué sur celle - ci , placer les points
« M » et M’ » . En déduire la valeur approximative du nombre
d’or.
1ère Façon :
Procédure à appliquer pour obtenir par le calcul du nombre d’or :
Après avoir tracé le
triangle ABC , rectangle en « B »
-
On
note AB = a
-
On
exprime AC en fonction de « a ».
-
On
déduit l’expression de « AM’ »
et « AM » en fonction de « a ».
- On calcule le rapport
![]() et l’on montre que le
nombre d’or est :
et l’on montre que le
nombre d’or est :
|
|
|
|
soit
|
|
2ème Façon :
On recherche de l’équation permettant de calculer
le nombre d’or :
On note
AB = a et ![]() = x
= x
-
On
exprime AM en fonction de
« a » et « x ».
-
En
utilisant la relation : 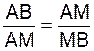 on montre
que a² -
on montre
que a² - 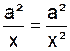
-
On
en déduit l’équation permettant de calculer le nombre d ‘or : x² -
x - 1
( l’équation obtenue
est une équation du deuxième degré).
|
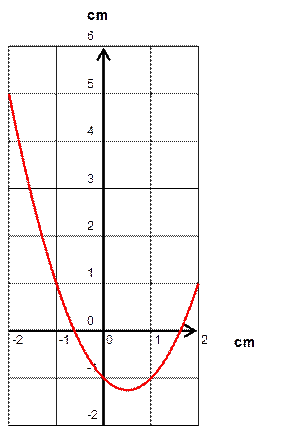
-
On construira la représentation graphique de la
fonction (@ info): -
f : x x² - x -1
et en déduire la valeur du nombre d’or (l’utilisation d’une calculatrice
graphique est conseillée) Voir le tracé ci
contre : Le point « x » = 1,618 pour y= 0
est une des solutions de l’équation ; la valeur négative n’est pas
retenue. ( @ INFO sur les
calculs) |
|
Il est évident qu’il
faut savoir résoudre algébriquement les équations du second degré pour trouver
un résultat.
|
|
III) APPLICATIONS : |
|
|
A) Partage d’un segment dans la divine proportion: |
|
F lire « phi »
Le nombre d’or
correspond à un rapport de grandeurs, entre elles et par rapport au tout.
C’est le partage
d’une longueur en deux parties inégales, dans lequel le rapport de la grande
partie au tout est égal au rapport de la plus grande partie à la plus petite.
|
Soit le segment de
droite AB et un point M, situé sur ce segment, permettant d’obtenir la
relation suivante : |
|
Les fractions ![]() ou
ou ![]() approchent ce
rapport. On prendra
approchent ce
rapport. On prendra ![]() = 1,618
= 1,618
Exemple 1 : Calcul de la
longueur totale du segment connaissant la plus petite dimension du
segment :
|
Soit MB = 10 cm Suivant la formule ci dessus : : AM = 10 × 1,618 = 16,18 Longueur totale du
segment AB : AB = AM + MB =
16,18 + 10 = 26,18 cm |
|
Exemple 2 : Calcul de la
longueur totale du segment connaissant la plus grande dimension du
segment :
|
Soit AM = 10 cm Suivant la formule ci dessus : : MB = 10 / 1,618 = 8,85 cm Longueur totale du
segment AB : AB = AM + MB = 10+
8,85 = 18,85 cm |
|
.
Division d’un segment
en deux parties , dans le rapport :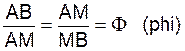
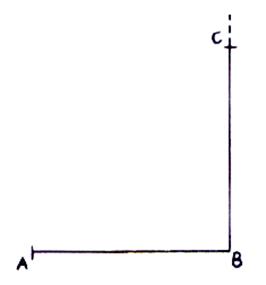
Avec un compas , et soit un segment AB
|
1-
Tracer la perpendiculaire BC de longueur AB à partir de
« B » 2-
|
2 - Diviser la droite BC en deux parties égales au
compas. Le point O est le point central.
|
|
|
|
|
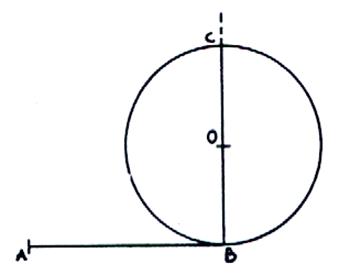
3-Tracer à partir
de O un circonférence de diamètre BC.
|
3-
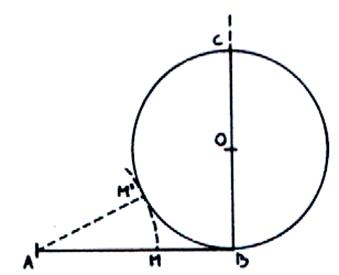
Tracer à partir de A un arc tangent extérieurement à la
circonférence de centre O qui la touche en « M’ » et qui coupe la
droite AB en « M » 4-
|
|
5- Le rapport
obtenu est
|
|
|
|
B
)Construction d’un
rectangle à partir des segments |
|
Pour construire un
rectangle d’or la méthode est la
même : le petit côté est dans le rapport
(phi) avec le grand côté. On peut
toujours vérifier les calculs en se servant du rapport approximatif 8/5 ou
21/13
Procédure :
1°) Tracer un segment de longueur « a » ;
2°) calculer la
longueur de la largeur ( a x 8/5 = 8 a
/ 5 ) ;
3°) tracer à
l’extrémité du segment tracé un segment perpendiculaire de longueur ( 8a / 5 ) ;
4°)
terminer le rectangle en traçant des parallèles aux côtés tracés.
|
|
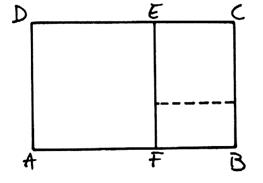
C) Construction d’un rectangle à partir du carrée |
|
Procédure :
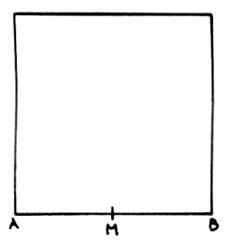
1- tracer un
carré
|
2- Diviser la base du carré en deux parties égales.
|
3- Avec le compas, tracer à partir de « M »
un arc de cercle qui passe par « C »
|
|
|
|
|
4-Du point
d’intersection de l’arc de cercle avec le prolongement de la base
« AB », « N » on trace la perpendiculaire à
« AB ». Elle coupera le prolongement du sommet du carré en
« N’ » |
|
|
5 -La relation
obtenue sera :
|
|
|
|
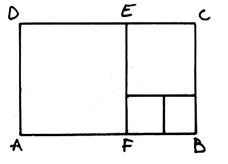
Pour agrandir :
Pour réduire :
|
- On trace un
rectangle ABCD qui est dans un rapport de
« phi » - On trace un carré
de côté AD à l’intérieur de ce rectangle. Remarque : Le
rectangle ECFB est lui aussi dans le rapport « phi » ; on peut
ainsi de suite réduire dans le rapport « phi ». |
||
|
|
|
|
|
@info |
|
|
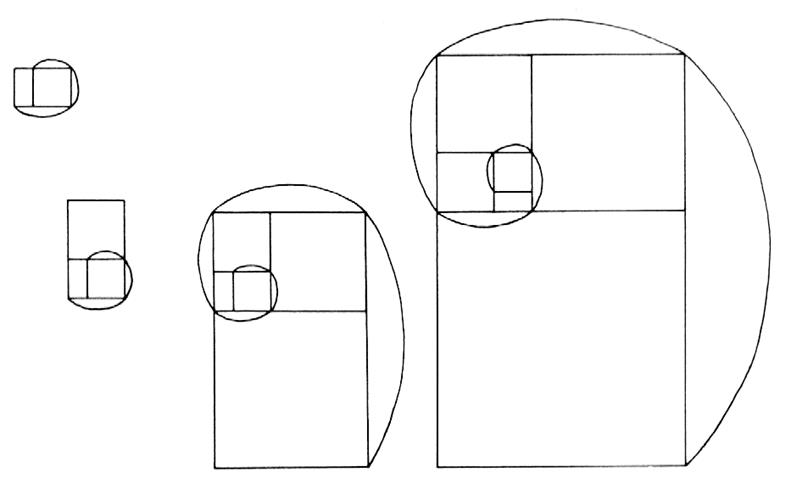
On se servira de
l’agrandissement du « rectangle d’or » pour tracer cette spirale
particulière. Il faut faire partir la ligne courbe d’un premier carré inscrit
dans un rectangle d’or. Elle doit toucher trois coins de ce carré et un coin
du rectangle. Puis on agrandit la spirale par le tracé d’un carré
d’agrandissement à partir de la plus grande dimension et ainsi de suite. |
|
|
On remarquera que les rapports des côtés des deux
pentagones est égal à « phi ».
Construction au compas :
|
1- tracer une circonférence dont le centre est O et le
diamètre AB |
2- A partir de O, en se servant d’une équerre, tracer
une perpendiculaire à AB qui coupe la circonférence en « D » |
3- Avec le compas diviser le rayon OB en deux parties
égales : ON = OB |
||
|
|
|
|
||
|
|
||||
|
4 - Mesurer au
compas la longueur ND et , en partant de
« N » tracer un arc de cercle qui viendra couper « AO »
en « M ». |
5- Mesurer la
distance « MD » au compas et reporter cette longueur sur la
circonférence. 6 - En réunissant
les points obtenus par des cordes, on reconstitue le pentagone convexe. |
|||
|
|
|
|||
|
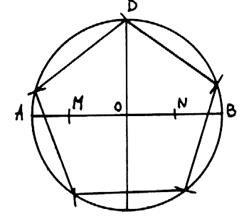
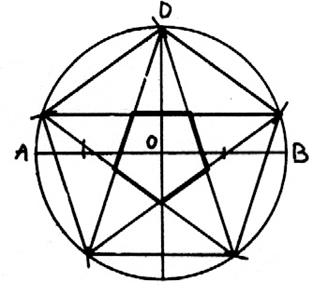
7 - Pour obtenir le
célèbre pentagone étoilé, on relie entre eux
tous les trois points. On a ainsi construit un second pentagone inversé. |
|
8- Le rapport des
côtés des deux pentagones est égal à « phi ». |
||
|
|
PARTIE 2 |
|
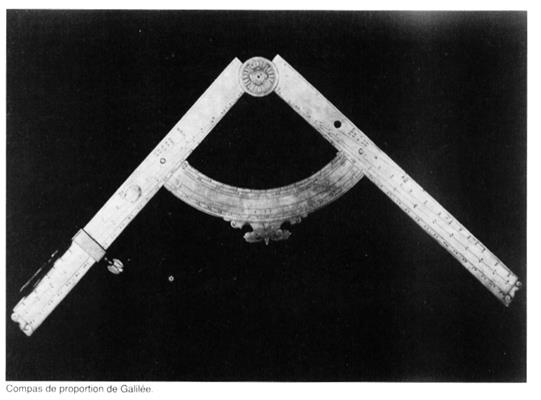
Compas de
proportion de Galilée |
|
Si le nombre d’or est
très célèbre, c’est surtout parce qu’il entre dans la construction de certains
polyèdres réguliers qui ont eu à certains moments de l’histoire une valeur
mystique ou symbolique à cause de leurs propriétés esthétiques ou géométriques : les
décagones et les pentagones. Sans doute la division en dix et en cinq tronçons égaux s’est - elle imposée par l’observation de la nature. Dans le
règne végétal, par exemple, se retrouve très fréquemment la répartition des
pétales d’une fleur par cinq, dont les extrémités forment entre elles un pentagone régulier.
Dans le règne animal,
l’oursin est un pentagone étoilé ;l’observation
de mains de l’homme , formées de cinq doigts, a certainement eu aussi une
influence sur l’importance accordée à ce
nombre. S’ y sont ajoutées des découvertes mathématiques et géométriques qui
ont fait de ces figures des sortes de constructions parfaites et mystérieuses.
Le pentagone étoilé , figure très répandues dans les
architectures des cathédrales et les signes et emblèmes de certains groupes ou
sectes , en témoigne.
Il est pratiquement
certain que le nombre d’or a été d’abord découvert par de nombreux tracés et
divisions de figures et que l’on a déduit des tâtonnements géométriques le
caractère mathématique du rapport de proportions du nombre d’or.
Car le nombre d’or
est en mathématique un nombre irrationnel parmi d’autres ,
c’est - à - dire un nombre irréductible à un rapport de nombres entiers ou à
une fraction. On nomme : 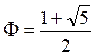 ;
;
Ce nombre qui a des
propriétés mathématiques et géométriques spécifiques.
Certains artistes ont
eu recours directement au nombre d’or dans la composition de leurs
œuvres : en poésie , en musique et dans les beaux
arts , l’associant ou non à des préoccupations
religieuses ou philosophiques .
Les exemples de
constructions à partir du nombre d’or vu précédemment sont destinées aux
peintres.
LA DIVISION en « MOYENNE » ET
« EXTREME » RAISON.
C’est ce que l’on
appelle : la « section dorée » :
La moyenne raison est le rapport entre
la petite et la grande dimension. L’extrême
raison est le rapport entre la grande dimension et la dimension totale.
Ces deux termes du
rapport sont égaux entre eux et égaux au nombre d’or.
|
|
Le compas, la règle
et l’équerre sont les instruments avec
lesquels on peut faire la division en moyenne et extrême raison. Plus
précisément, on se servait du compas de proportion pour calculer le nombre
d’or. Ce compas est constitué de deux règles graduées ,
articulées à une de leurs extrémités. L’ouverture du compas placé sur une
longueur donnée, les graduations indiquent la réduction ou l’agrandissement
proportionnel correspondant. ► il est
établi une fois pour toutes que ►Il s’agit
toujours d’un partage asymétrique d’une dimension en deux parties :une moyenne et une petite dimension. |
NOTA : il faudra , à partir de ces données , dans le cadre d’un
travail artistique apprendre à « composer selon le nombre d’or ».
Voir aussi les formats « marines »