|
PARTIE 1 |
Travaux
auto - formatifs: niveau IV
.(BAC…) sur LE
NOMBRE D’OR |
TRAVAIL PERSONNEL : De
ces travaux , un devoir peut être donné : les exigences et les difficultés
à résoudre sont fonction du niveau des objectifs à atteindre.(pré défini par le
programme)
|
|
ٱ |
Questionnaire 1
|
|
ٱ |
Questionnaire 2
Activité 1 ; activité
2 ; activité 3 A et activité
3B
|
|
ٱ |
|
(@) |
A) Partage d’un segment dans la divine
proportion: |
ٱ |
Activité 4 ; activité
5 ; activité 6 ;
|
|
B) Construction
d’un rectangle à partir des segments |
ٱ |
-
calcul : activité 7 activité 8
|
|
C ) Construction
d’un rectangle à partir d’un carré. |
ٱ |
-
Activité
9
|
ٱ |
Activité 10 ; activité
11
|
|
ٱ |
Activité 12
Activité 13
|
PARTIE
2 |
ٱ |
Questionnaire N° 3
Activité 14
SUITE à donner à ce cours: Pour donner un prolongement et assurer un travail
en interdisciplinarité, en Art appliqué, on devra traiter de la « composition selon le nombre
d’or ».
|
|
ٱ |
QUESTIONNAIRE 1 :
|
|
|
1°) Qui est « Vitruve » ( quelle
période) ?
2°)
donner la citation de « Vitruve » concernant l’obtention du « nombre d’or »:
3°) de quoi parle - t- il ?
4°) de quelle façon a - t -
on découvert le nombre d’or ?
5°)
Qui a attribué les propriétés au
nombre d’or ?
.
6°) A partir de quel événement a -t - on
fait l’usage de la division au
nombre d’or ?( à quelle période ? )
7°) que précise t - il ? :
8°) A quelles figures géométriques
lie - t- on le nombre d’or ?:
9°)
Rechercher les définitions :
de « pentagone » ;
« polygones réguliers » ; « polyèdres » ;
Rechercher les figures ou autres dessins.
10°)
Compléter les phrases :
Empreint de mystère, objet de culte
tantôt religieux , tantôt magique , le nombre d’or influence la vision ………………………………………….
Chez les Grecs , avec le
développement de la géométrie , la secte secrète des pythagoriciens en avait
fait ………………………………………………………………………………………………………………………………….
Architectes , peintres et sculpteurs
cherchant à renouer avec ……………….. se sont réclamés de la doctrine …………………des corps cosmiques , ………………………………………..
, et on fait du nombre d’or , « ……………………. »,
un modèle …………………………………………….
Le nombre d’or correspond à une
proportion particulièrement esthétique
appelée « ………………………………… » ;
il tient toujours une place importante dans le monde des arts et de
l’architecture.
11 °) Quelle est la figure
géométrique qui permet d’approcher et de
comprendre la « divine
proportion » ?
12 °) A quel
format des « peintres » correspond - t-il ?
13°) Trouver des professions ou
activités où l’on utilise le nombre
d’or ?
|
|
|
QUESTIONNAIRE 2 :
A)
Recherche du nombre d’or à partir de la définition :
1°) Par quelle lettre désigne - t - on
le nombre d’or , comment la note - t -on ?
2°) Donner la définition du nombre
d’or :
.
3°) Soit le segment de droite AB et un point M, situé sur ce
segment : établir la relation qui permet d’obtenir le nombre d’or :
|
|
|
4°) Comment s’appelle cette relation ?
5°) A quelles fractions peut approché ce rapport ?
Activités : niveau IV (dont : Bac. Prof)
Recherche du nombre d’or :
On prend appui sur la construction
de la « divine proportion » :
|
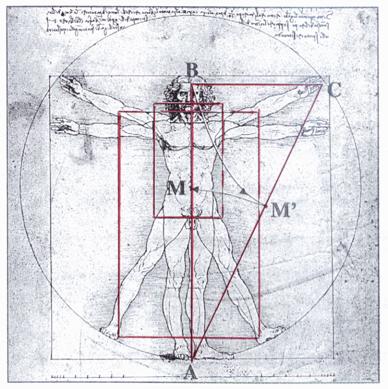
La distance AB entre les pieds et
la tête de l’homme présentant les mensurations idéales et dessiné par Léonard
de Vinci, est partagée par le nombril « M » dans une proportion
correspondant au nombre d’or. La construction de la
« divine proportion » prend appui sur le triangle rectangle
ABC rectangle en « B » tel
que : BC = Sur le dessin ci-contre , sont
représentés des rectangles dont le rapport entre la longueur et la largeur
est égal au nombre d’or ; de tels rectangles sont appelés « rectangles d’or » |
|
1°)
détermination par le tracé de la
position du point « M » sur la segment AB de telle sorte que :
![]()
Tracer un triangle rectangle
semblable à celui de la figure
« ABC », puis, en utilisant le principe de construction
indiqué sur celle - ci, placer les points « M’ » et M » . En
déduire la valeur approximative du nombre d’or.
Activité 1 : Relever les longueurs des segments
AB ; AC ; AM ; AM ’
et calculer le rapport ![]() et le rapport
et le rapport ![]() ;le rapport
;le rapport
![]() et
et ![]() ; comparer les
résultats et conclure que :. …………………………………………
; comparer les
résultats et conclure que :. …………………………………………
Activité 2 :
Après avoir tracé un triangle ABC , rectangle en « B »
- On note AB = a
- On demande : Calculer
AC² ; puis exprimer AC
en fonction de « a » :
- On demande : En déduire
l’expression de « A M’ »
et « AM » en fonction de « a ».
4. On demande Calculer le rapport ![]() et l’on montre que le
nombre d’or est :
et l’on montre que le
nombre d’or est :
![]() ou soit
ou soit ![]() ≈ 1,618
≈ 1,618
Activité 3 :
A)
Rechercher l’équation permettant de
calculer le nombre d’or par la résolution d’une équation du second degré.
( voir le triangle ABC sur le dessin
de Vinci)
On donne : AB = a
et ![]() = x
= x
a) Exprimer AM en fonction de « a » et « x ».
b) En utilisant la relation : ![]() on montrer que
« a² -
on montrer que
« a² - ![]() » (1)
» (1)
c) En déduire l’équation du second
degré permettant de calculer le nombre d’or et la résoudre. « x² - x -1 »
(c’est une activité de niveau
(Bac. Prof) ;pour cela Il est évident qu’il
faut savoir résoudre algébriquement les équations du second degré .
B) Résoudre graphiquement l’ équation
« y = x² - x -1 » , situer sur la courbe
position du nombre d’or.
|
construire la représentation
graphique de la fonction : f : x x² - x -1 et en déduire la valeur
du nombre d’or. (l’utilisation d’une calculatrice graphique est conseillée) |
|
.
|
|
III)
APPLICATIONS : |
|
|
A)
Partage d’un segment dans la divine proportion: |
|
|
Soit le segment de droite AB et un
point M, situé sur ce segment, permettant d’obtenir la relation
suivante : |
|
Les fractions ![]() ou
ou ![]() approchent ce rapport. On prendra
approchent ce rapport. On prendra
![]() = 1,618
= 1,618
Activité 4 : Calculer la longueur totale
du segment connaissant la plus petite dimension du segment :
|
Soit MB = 10 cm ; calculer AB |
|
Activité 5 : Calculer la longueur totale du segment
connaissant la plus grande dimension du segment :
|
Soit AM = 10 cm
, calculer AB |
|
.
Activité 6 :Diviser , par tracé , un
segment AB en deux parties , dans le rapport :![]() ; Avec un compas .
; Avec un compas .
|
|
B )Construction
d’un rectangle à partir des segments |
|
Pour construire un rectangle
d’or la méthode est la même : le
petit côté est dans le rapport
(phi) avec le grand côté. On peut
toujours vérifier les calculs en se servant du rapport approximatif 5/8 ou 13 / 21.
(@ Voir tracé d ‘un rectangle)
Activité 7 : On donne la longueur du
petit côté d’un rectangle : 12 cm
; tracer le rectangle dans le format marine.
Activité 8 On donne la longueur du grand
côté d’un rectangle : 27 cm ;
tracer le rectangle dans le format marine.
|
|
C)
Construction d’un rectangle à partir du carrée |
|
Activité 9: Soit un carré de 9 cm de côté , tracer le rectangle d’or à
partir de ce carré .
|
|
Activité 10:Sur une feuille A3 : tracer le rectangle d’or ABCD :
22 x 12 cm ; Agrandir ce rectangle , en vue d’obtenir un autre rectangle
d’or.
|
Activité 11 - On trace un rectangle ABCD qui est dans un rapport de « phi » : 22 x 12 cm - tracer à l’intérieur de ce rectangle un autre
rectangle d’or . |
||
|
|
|
|
|
@info |
|
Activité 12: Sur une feuille de format
A4 ; centrer un rectangle d’or de 4,6 x 2,7 cm, à partir de ce
rectangle tracer une spirale harmonique.
La plus grande possible.
Activité 13: tracer un pentagone convexe , (
diamètre AB = 10 cm) et a partir du même tracé construire le pentagone étoilé .
(noter par une lettre chaque sommet et établir un rapport qui vérifie que «les
rapports des côtés des deux pentagones est égal à
« phi » ».
|
|
PARTIE 2 |
QUESTIONNAIRE N°3 :
1°) Compléter la phrase
suivante : le nombre d’or est en
mathématique un nombre ……………………….., c’est - à - dire un nombre irréductible à un
rapport de nombres entiers ou à une fraction.
2°) Qu’appelle - t- on
: LA DIVISION en
« MOYENNE » ?
3°) Qu’appelle - t- on : « EXTREME » RAISON. ?
4°) Qu’appelle - t- on :
« section dorée » ?
5°) Quel point on en commun LA
DIVISION en « MOYENNE » et
« EXTREME » RAISON.
6°) Avec quels instruments peut -
on faire la division en moyenne et
extrême raison ?
7°) Quel autre outil peut -on utilisé
, comment le nomme t - on ; précisez?
Activité 14: :
|
|
Travail de recherche : Rechercher une reproduction d’une oeuvre
(peinture ou photographie d’un monument architectural,.. ; )
« Composer selon le nombre d’or ». Le montrer sur la reproduction
et expliquer. |