|
PARTIE 1 |
CORRIGE sur LE NOMBRE D’OR |
Activités : niveau IV (dont : Bac. Prof)
Recherche du nombre d’or :
On prend appui sur la construction
de la « divine proportion » :
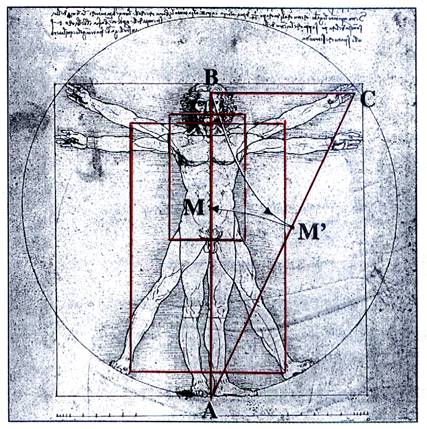
|
La distance AB entre les pieds et
la tête de l’homme présentant les mensurations idéales et dessiné par Léonard
de Vinci, est partagée par le nombril « M » dans une proportion
correspondant au nombre d’or. La construction de la
« divine proportion » prend appui sur le triangle rectangle
ABC rectangle en « B » tel
que : BC = Sur le dessin ci-contre , sont représentés des rectangles dont le rapport
entre la longueur et la largeur est égal au nombre d’or ; de tels
rectangles sont appelés « rectangles d’or » |
|
1°)
détermination par le tracé de la
position du point « M » sur la segment AB de telle sorte que :
![]()
Tracer un triangle rectangle
semblable à celui de la figure
« ABC », puis, en utilisant le principe de construction
indiqué sur celle - ci, placer les points « M’ » et M » . En déduire la valeur approximative du nombre d’or.
Activité 1 : Relever les longueurs des segments
AB ; AC ; AM ; AM ’
et calculer le rapport ![]() et le rapport
et le rapport ![]() ;le rapport
;le rapport ![]() et
et ![]() ; comparer les
résultats et conclure que :. Les rapports
sont égaux
; comparer les
résultats et conclure que :. Les rapports
sont égaux
Activité 2 :
Après avoir tracé un triangle ABC , rectangle en « B »
- On note AB = a
- On demande : Calculer AC² ; puis exprimer AC en fonction de « a » :
AC² = ( a² + (![]() ) ² ) = a² +
) ² ) = a² + ![]() =
= ![]()
AC = ![]() =
= ![]()
- On demande : En déduire
l’expression de « A M’ »
et « AM » en fonction de « a ».
AM’ = ![]() -
-![]() ou
=
ou
= ![]() = AM ;
AM =
= AM ;
AM = ![]()
4. On demande Calculer le rapport ![]() et l’on montre que le
nombre d’or est :
et l’on montre que le
nombre d’or est :
![]() ou soit
ou soit ![]() ≈ 1,618
≈ 1,618
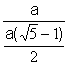 =
= ![]() =
= ![]() =
= 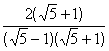 =
=![]() =
= ![]() =
=![]() =
=![]()
Conclusion: ![]() =
= 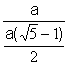 =
=![]()
Activité 3 :
A)
Rechercher l’équation permettant de
calculer le nombre d’or par la résolution d’une équation du second degré.
( voir le triangle ABC sur le dessin de Vinci)
On donne : AB = a
et ![]() = x
= x
a) Exprimer AM en fonction de « a » et « x ». :
puisque ![]() donc
donc ![]()
b) En utilisant la relation : ![]() on montrer que
« a² -
on montrer que
« a² - ![]() » (1)
» (1)
Il faut trouver MB = AB - AM = a -
![]()
on remplace
« AB » ; « AM » et « MB » dans le
relation ![]()
on obtient : 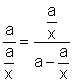 ; en faisant le produit en croix : a (a -
; en faisant le produit en croix : a (a - ![]() )= (
)= (![]() )² (2)
)² (2)
soit : en développant (2) on
obtient la relation (1) :
a (a - ![]() )= (
)= (![]() )² = a² -
)² = a² - ![]() (3)
(3)
c) En déduire l’équation du second degré
permettant de calculer le nombre d’or et la résoudre.
1°) Réduire la relation précédente (3) au même
dénominateur : ![]() = 0
= 0
(@ info + »on chasse les dénominateur »++) (d’après
un théorème sur les égalités :cela revient à multiplier tous les termes
par x² )
On obtient
l’équation : a²
x² - a² x - a² = 0 ;
2°) On factorise : a² (x² - x -1) = 0
3°) Il faut
résoudre l’équation « x² - x - 1 » , une solution de cette équation est le nombre d ‘or. (On doit résoudre une équation du
deuxième degré).
4°) Résoudre l’équation : x² - x -1
(c’est
une activité de niveau (Bac. Prof) ;pour cela Il est évident qu’il
faut savoir résoudre algébriquement les équations du second degré .
Résolution :
Δ = b²
- 4ac ; (-1)² - 4 fois (+1)
fois (-1) = 1 + 4 = 5
X’ = ![]() soit x ‘ =
soit x ‘ =
![]() et x’’=
et x’’= ![]() soit x’’=
soit x’’= ![]()
On retiendra la solution
« positive » : ![]() que l’on
appelle : phi et que l’on note :
que l’on
appelle : phi et que l’on note :![]()
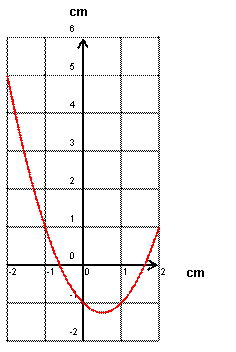
B) Résoudre graphiquement l’ équation « y
= x² - x -1 » , situer sur la
courbe position du nombre d’or.
|
construire la représentation
graphique de la fonction : f : x x² - x -1 et en déduire la valeur
du nombre d’or. (l’utilisation d’une calculatrice graphique est conseillée) Voir le tracé ci contre : Le point
« x » = 1,618 pour y= 0 est une des solutions de
l’équation ; la valeur négative n’est pas retenue. |
|
.