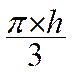|
Le
trapèze |
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : |
Objectif
suivant : |
|
|
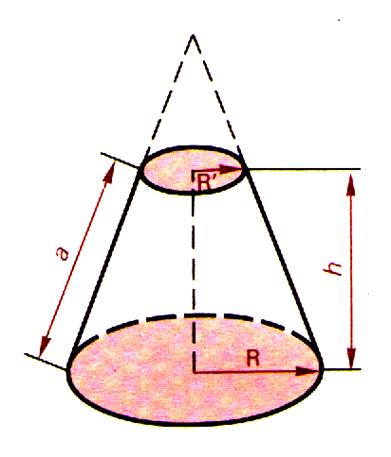
DOSSIER : Tronc de cône : calculs du Volume et aire du tronc de cône . |
|
|||||
|
|
Définition. |
|
|||||
|
|
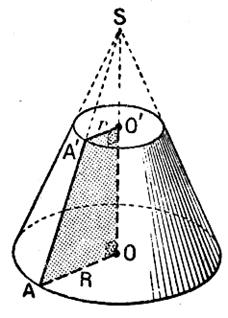
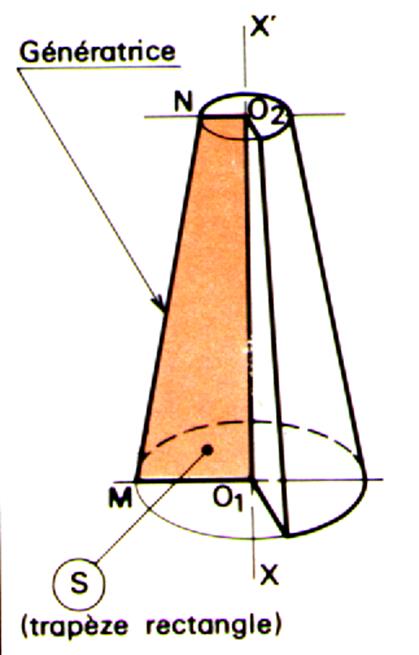
Le tronc de cône de révolution. |
|
|||||
|
|
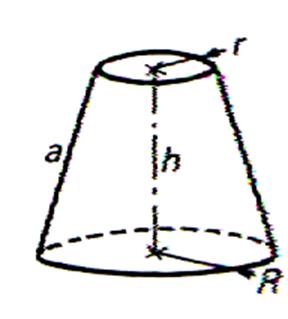
Volume du tronc de cône . |
|
|||||
|
|
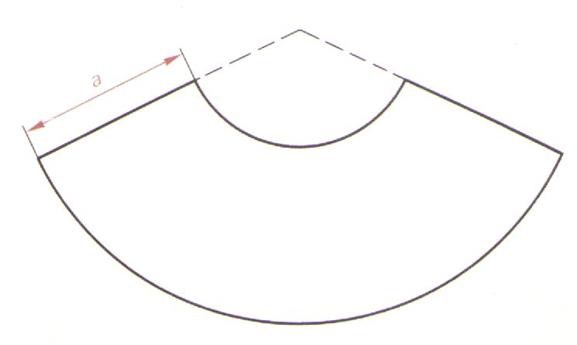
Aire latérale du tronc de cône. |
|
|||||
|
|
Situations Problèmes . |
|
|||||
|
|
|
|
|||||
|
|
|||||||
|
TEST |
COURS |
Interdisciplinarité |
|
||||
|
|
TRAVAUX
AUTO FORMATIFS. |
|
||
|
|
CONTROLE : Dessiner un tronc de
cône en perspective
. Donner la formule
permettant de calculer le volume du tronc de cône . Donner la formule permettant
de calculer la surface latérale du tronc de cône EVALUATION 1°) Soit un tronc de cône : h = 15 cm ;
R = 5cm ; R’ = 2cm ; calculer son volume Calculer son aire latérale. 2°)Soit un tronc de
cône : a = 15 cm ; R = 5cm ; R’ = 2cm ; Calculer son aire
latérale. 3°) voir
« trigonométrie » :
La figure ci - dessous représente un tronc de cône
dont la grande base est un disque de 46 mm de diamètre et la petite base un
disque de 28 mm de diamètre
. la hauteur de ce cône est de 50 mm .
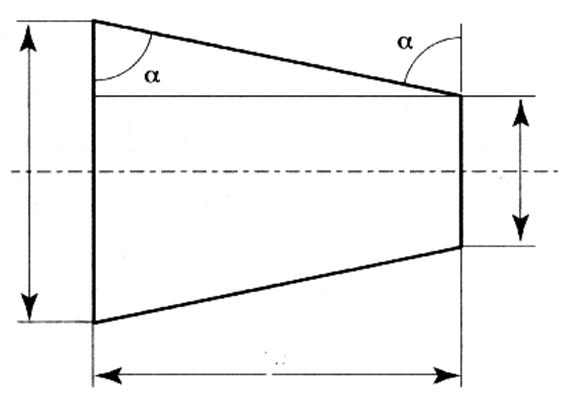
Calculer l’angle « alpha »
. Il faut calculer des éléments du triangle rectangle dont un angle est a
. 4°)
Problème : Une grume de sapin de 4’20 m de longueur mesure à
ses extrémités 6O cm et 40 cm de diamètre. 1°) Calculer son volume réel en lui appliquant la
formule du tronc de cône. (prendre pi
= 22/7) 2°) Calculer le volume de la grume en assimilant
celle-ci à un cylindre dont le diamètre serait la moyenne des diamètres des
deux extrémités . 3°) On extrait de cette bille de bois une poutre de section carrée de côté 28 ; Calculer : c)
le volume de la
poutre. d)
Le rapport du volume
de la poutre à celui de la grume , calculé au 2ème
. |
|
||
|
|
|
|
||
|
|
|
|