|
|
|
|
INFO :Disque |
|
|
Le cercle et
disque |
|
|
Circonférence |
|
|
|
|
ENVIRONNEMENT du dossier:
|
Index warmaths |
Objectif
précédent : 1°) Le cercle ( découverte en primaire) 2°) |
Objectif suivant |
|
|
|
|
|
|
|
|
|
|
|
|
|
DOSSIER : AIRE DU
DISQUE (primaire) |
|
|
|
Activité 1 : l’ aire
d’un carré |
|
|
|
Activité 2 : évaluation de l’aire d’un disque . |
|
|
|
Calcul
de l’ aire du disque Relation mathématique de
calcul : |
|
|
|
Situations problèmes. |
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité : 2.
travaux
6ème |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Activité 1 |
|
||||||||||||||||||
|
|
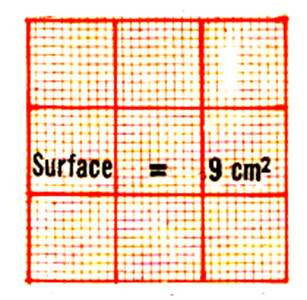
Traçons un carré de 3cm de côté : Observons : Il
contient 9 carrés de 1 cm de côté ;
Son
aire est 9 cm2 |
|
||||||||||||||||||
|
|
Activité 2 : |
|
||||||||||||||||||
|
|
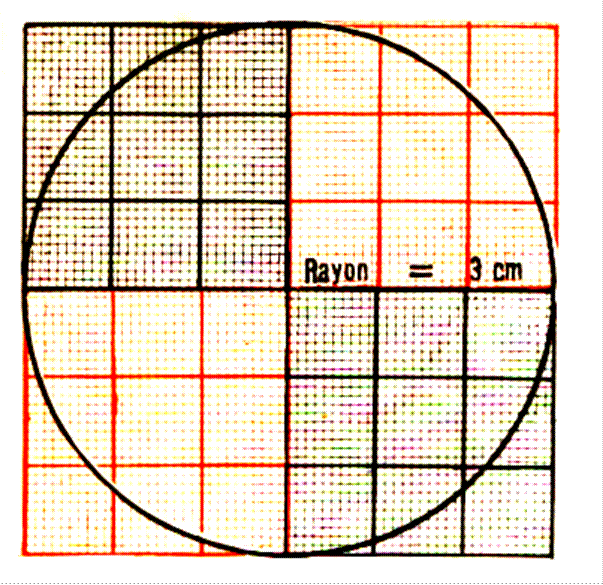
Tracer un cercle de rayon 3 cm . L’ensemble de tous les points du plan à l’intérieur du cercle (cercle
compris) est appelé : disque Pour déterminer l’aire du disque nous pouvant
utiliser deux procédures :
Par comptage ( addition) des carrés
élémentaires avec une estimation
approximative des ¼ ; ½ ; 3 /4 de carré Cette somme donne une valeur approchée de la valeur de l’aire. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
On dit que ce cercle est tangent aux côtés du carré
, puisqu’il est tangent alors on dit aussi que le carré est
« inscrit » au carré. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
En première approximation : La surface du carré ayant pour côté le rayon du cercle : 3 Le disque ne couvre pas 4 carrés . Sa surface est inférieure à 9 cm2 |
|
||||||||||||||||||
|
|
On
considère « pratiquement » que la surface de ce cercle est égale à 9 cm2 |
|
||||||||||||||||||
|
|
A
partir du tracé ci – dessus : la
surface égale à celle du disque se résume à : 3 fois 9 plus 1 + ¼ de
carré +1/100 de carré : Soit 27 + 1 + 0,25 +0,01 = 28, 26
carré de 1cm de côté. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Relation
mathématique de calcul : |
|
||||||||||||||||||
|
|
Aire du disque =
« Rayon »
fois
« Rayon » fois
« 3,14 » Si l’on remplace « Aire du
disque » par
l’abréviation «AD » et « Rayon » par la lettre
« R » , on obtient une formule Telle que AD = R |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
EXERCICES : 1° Compléter le tableau :
|
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
Situations problèmes. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
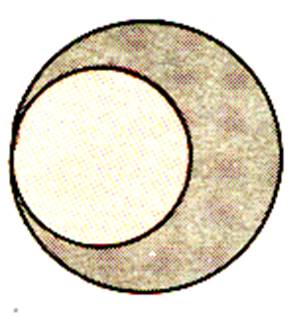
1°)Découper un disque gris de 12 cm de
diamètre et un disque rouge de 4cm . Calculer l’aire de chaque disque. Quelle est l’aire de la surface
de la partie grise encore visible ?
|
|
||||||||||||||||||
|
|
Remarquer que l’aire est toujours la même quelque
soit la place du disque rouge sur le disque gris. La surface grise recouverte est égale à la surface du disque rouge . |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
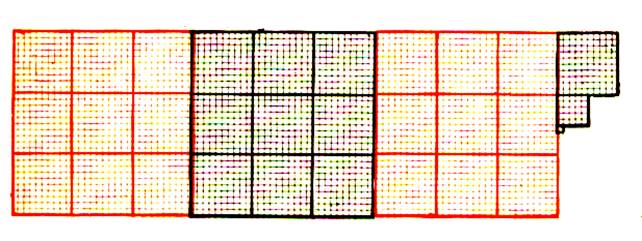
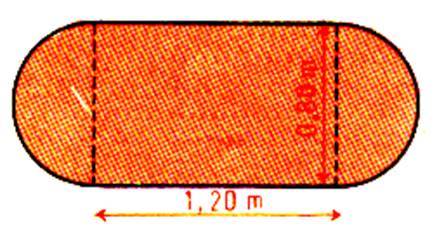
2°) On
découpe dans une plaque un panneau
ayant la forme ci – contre :. Rectangle : longueur : 1,20 m ; Largeur 0,80 m 1°)Quelles figures géométriques déjà étudiées
retrouve - t – on dans ce
panneau ? 2°)Quelle est l’aire de ce panneau ? 3°) quelle est sa masse si 1 m2 du panneau pèse 3,4 kg.
|
|
||||||||||||||||||
|
|
3°) Expliquer comment vous aller calculer l’aire de la surface grisée.
|
|
||||||||||||||||||
|
|
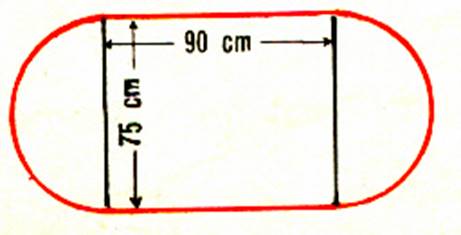
4°) On découpe dans une plaque un panneau ayant la forme ci –
contre :. 1°)Quelle est l’aire de ce panneau ? 2°) quelle est sa masse si 1 m2 du panneau pèse 1,7 kg
|
|
||||||||||||||||||
|
|
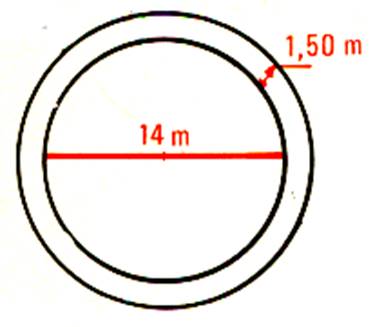
5°) Calculer l’aire du grand disque ; calculer l’aire du petit
disque. Soustraire les deux résultats : à quelle aire correspond ce
résultat ?
|
|
||||||||||||||||||
|
|
6°) Le diamètre = 1m ; calculer le périmètre du cercle et l’aire du disque. |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS. |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
CONTROLE : 1 ) A
quoi est égale l’ aire du disque ? 2 )
Donner la formule permettant de calculer l’aire d’un disque (compléter avec
un dessin coté ) EVALUATION
Donner les formules ;
remplacer les lettres par les valeurs données ,
faire les calculs Compléter le tableau
suivant :
|
|
|||||||||||||||||||||||||
|
|
|
|