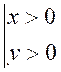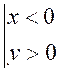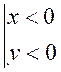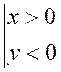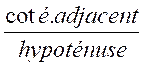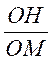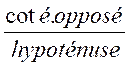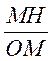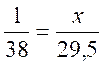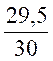|
Variation des nombres trigonométriques |
|
|
Pythagore |
|
|
Sinus dans le triangle
rectangle |
|
|
Cosinus dans le triangle rectangle |
ENVIRONNEMENT du dossier:
DOSSIER : COSINUS et SINUS d’un réel ,
dans le cercle trigonométrique .
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
I
) Repérage et coordonnées d’un point dans un
cercle trigonométrique. |
|
|||||
|
|
|
||||||
|
|
III)
Cosinus et sinus dans le deuxième quadrant . |
|
|||||
|
|
I V ) Etude du signe
du « sinus » et « cosinus » dans les quadrants du cercle .
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
||||
COURS
Nota : dans
le cercle trigonométrique les axes de «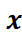 » et «
» et « 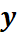 » sont perpendiculaires
» sont perpendiculaires
|
Le cercle trigonométrique est
divisé en quatre
parties ou quadrants. |
|
|
|
|
|
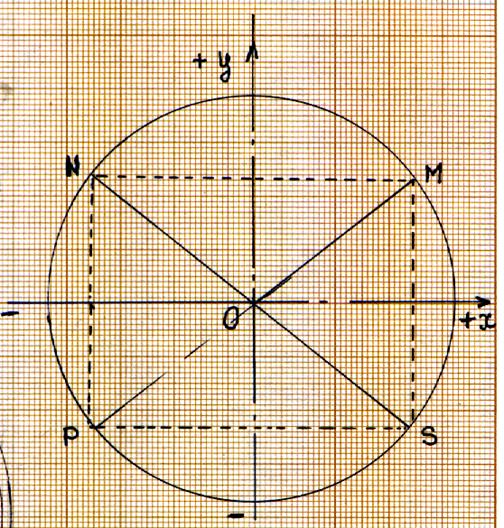
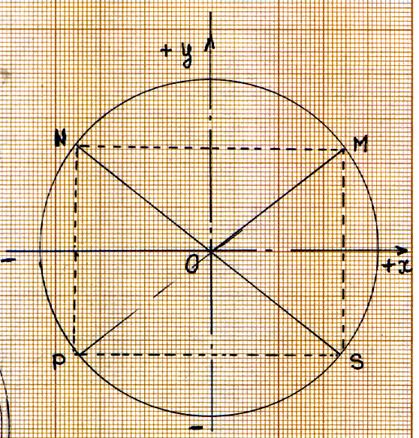
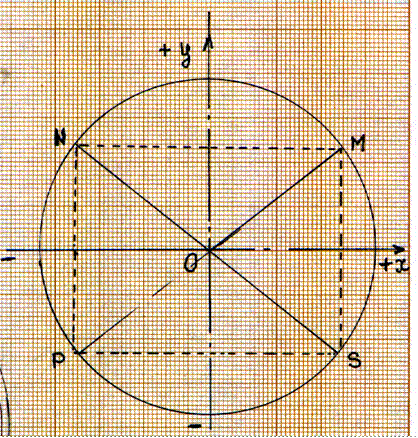
I ) Repérage et coordonnées d’un
point dans un cercle trigonométrique. |
|
|
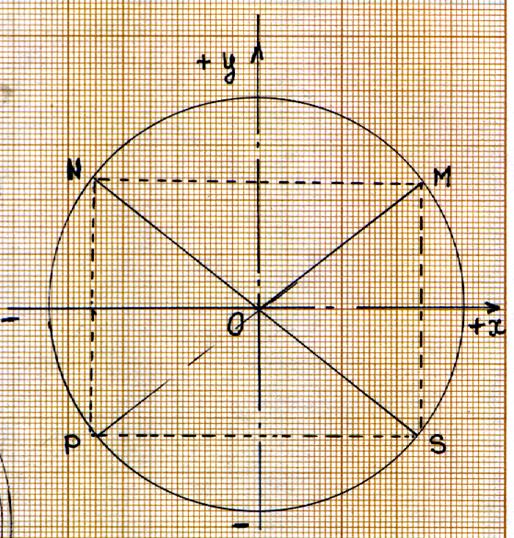
Le
point « M » appartient au premier cadrant : les coordonnées du point
« M » sont positives. M Le
point « N » appartient au deuxième
cadrant : N Le
point « P » appartient au troisième
cadrant : P Le
point « S » appartient au deuxième
cadrant : S |
|
|
|
|
||||
|
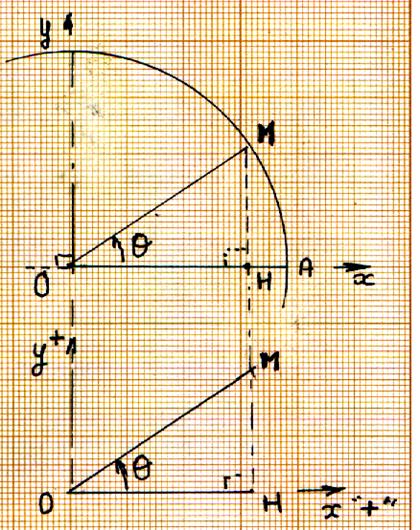
y Le « cosinus de l’angle Le « sinus de l’angle que l’on note M( cos q ;
sin q ) Justifications :
(voir le triangle rectangle) : Cosinus = ? cos q = d ‘ où : cos q = x Sinus = ? sin q = d’ où : sin q = y Recherche de la valeur du cosinus à partir d’un tracé : 1° ) Il faut relever sur le tracé les
longueurs de OM = 38 mm et OH = 29,5 mm 2°) « 1 » divisé par
la longueur du rayon = valeur du sinus (x) divisé par la longueur de MH : soit : avec la calculatrice on obtient la valeur de l’angle : cos 0,7763157 = 39°4’3’’ d’où q = 39°4’3’’
(à vérifier ; faire la même chose pour trouver le sinus q) |
|
||||
|
|
|||||
|
III
) Cosinus
et sinus dans le deuxième quadrant . |
|
||||
|
|
|
||||
|
x y N ( - |x| ; y ) N ( - |cos
q| ; + |sin q| ) D’où : L’abscisse de « N » = HO =- |cos q| Coordonnée de « N » = HN = + |sin q| |
|
||||
CONTROLE :
|
1°) |
|
|
A ) Nommer l’ axe des
cosinus et l’axe des sinus . B ) Pour les quatre
points (M ;N ;P ;S): Donner le signe de leur
coordonnées. |
|
2° ) Donner le signe du
sinus et cosinus d’un point situé dans
les quatre quadrants du cercle trigonométrique
EVALUATION
|
Travail sur papier millimétré : |
|
|
Mesurer la longueur du rayon ( vous devriez
trouver environ ;38 mm) ce rayon à pour valeur « 1 ». Question : Trouver la valeur approchée du sinus
et cosinus de « M » Exemple : Recherche de la valeur du
cosinus à partir d’un tracé : 1° ) Il faut relever sur
le tracé les longueurs de OM = 38 mm et OH = 29,5 mm 2°)
« 1 » divisé par la longueur
du rayon = valeur du sinus (x) divisé par la longueur de MH : soit : avec la calculatrice on obtient la valeur de l’angle : cos 0,7763157 = 39°4’3’’ d’où q = 39°4’3’’ (à vérifier ;et
faire la même chose pour trouver le sinus q) |