3^ème

Fiches :      L  ‘ Addition vectorielle .

Fiche 1 : Somme de deux vecteurs.

Fiche 2 : Autre façon de construire un représentant du « vecteur-somme ».

Fiche 3 : Propriétés de l’addition vectorielle.

Fiche 4 : Relation de Chasles.

Fiche 5 : Exercices .

3^ème

Fiches :      L  ‘ Addition vectorielle .

Fiche 1 : Somme de deux vecteurs.

Info +++

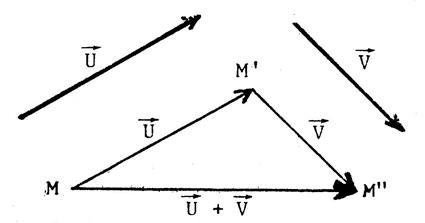
Vous avez vu dans la leçon « sur les vecteurs –fiche 6 » que :

Etant donné deux vecteurs    et  , la composée de la translation de vecteur    et de la translation de vecteur  est une translation.

Son vecteur est désigné par      ,et l’on appelle le vecteur- somme de   et  de   .

L’opération qui , à deux vecteurs , fait correspondre leur somme s’appelle :  « addition vectorielle ».

A retenir :

Pour construire un représentant du vecteur-somme de deux vecteurs   et   on choisit des représentants de   et de   de telle sorte que l’extrémité du premier coïncide avec l’origine du second.

Le représentant de      on a alors

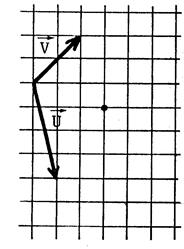
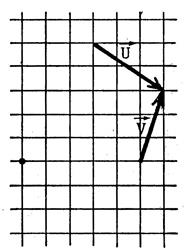
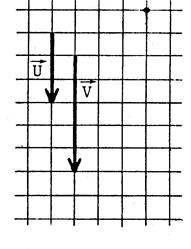
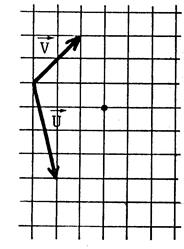
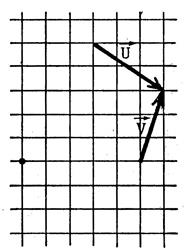
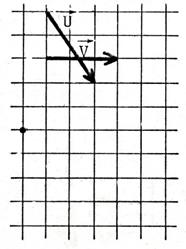
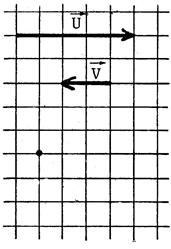
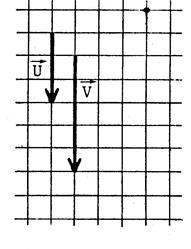
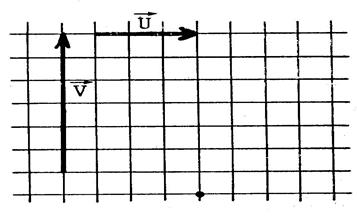
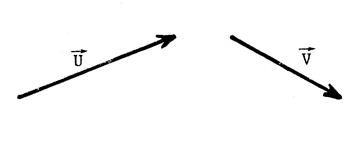
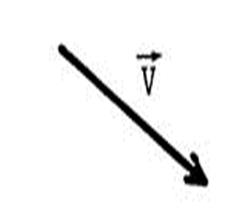
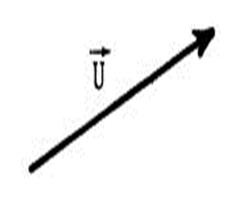
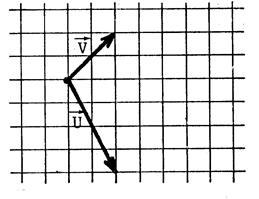
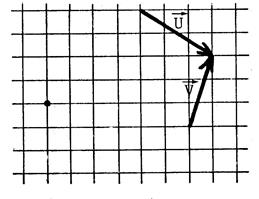
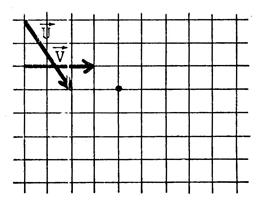
Exercices : Dans chacun des cas ci-dessous , dessinez  un représentant de        .

L’origine du tracé est matérialisé par un point .

Fiche 2 : Autre façon de construire un représentant du « vecteur-somme »

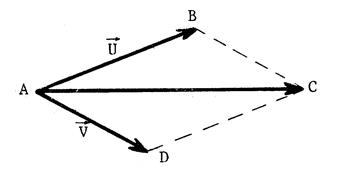
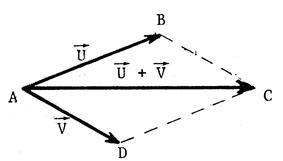
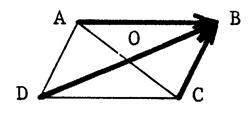
Etant donné deux vecteurs    et   , choisissons des représentants de    et de    de même origine « A ».

Soit « B » tel que    et  « B » tel que   .

Construisez le point « C » tel que « ABCD » soit un parallélogramme .

On a alors

D’après la fiche « 1 » , on peut écrire :      

Mais comme   alors :         et vous remarquez que   est une diagonale  du parallélogramme « ABCD ».

A retenir :

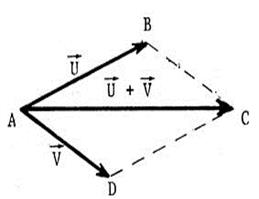
Pour construire un représentant du « vecteur-somme » de deux vecteurs   et   , on choisit des représentants de   et de     de même origine « A ».

que    et  . On construit le point « C » tel que « ABCD » soit un parallélogramme  le représentant de      d’origine « A » alors pour extrémité le point « C ».

Exercice 1 : Dans chacun des cas , dessinez un représentant de       . ( Utilisez la méthode ci-dessus )

L’origine du tracé est matérialisé par un point .

Exercice 2 : « A » , « B » ,  « C »  étant trois point du plan, construisez dans chacun des cas un représentant du vecteur-somme correspondant . ( Utilisez la méthode la plus simple.)

Fiche 3 : Propriétés de l’addition vectorielle.

Info ++++

« Commutativité » : 

  et   sont deux vecteurs quelconques.

Construisons un représentant de          par la deuxième méthode.

Que l’on place d’abord le représentant de    puis le représentant de   , ou le représentant de    d’abord , puis le représentant de   , la figure est la même.

ON peut donc dire :          

Pour tout vecteur   ,     ,                                  

L’addition vectorielle  est  commutative.

« Associativité » .

    sont trois vecteurs quelconques.

On a représenté ci-dessous deux fois la même figure.

Figure 1

Figure 2

Vous allez dessiner un représentant de      ( fig.1) et  de    )    (fig.2)

Sur  fig. 1           .                 ;           complétez le dessin .

Sur  fig. 2           .                 ;           complétez le dessin .

Vous en déduisez :

    )

Pour tous vecteurs        ,        )   , l’addition vectorielle est  « associative » .

On convient d’écrire :         à la place de        ou    de       )  

Elément neutre :

  est un vecteur quelconque . Choisissons  deux points « E » et « F » tels que  .

Vous savez que     et que    .On peut donc écrire :

Pour tout vecteur    ,              et    

Le vecteur nul est l’élément neutre  pour l’addition vectorielle.

Opposé d’un vecteur .

 est un vecteur quelconque.

Choisissons « A » et « B » tels que

Pour tout vecteur    , il existe un  vecteur que l’on appelle     « opposé de » noté   « Opp. de » tel  que :

  et      

Activité :

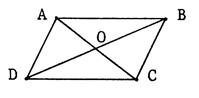
« ABCD » est un parallélogramme de centre « O ».

Démontrez que

Fiche 4 : Relation de Chasles

Info ++++

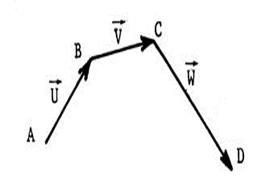
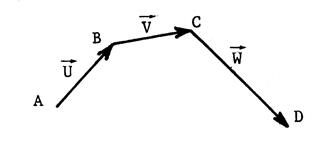
Reprenons la construction de   étudiée dans la « fiche 1 » .

On peut  écrire que :

Théorème :  « A » , « B » , « C » étant des points quelconques du plan : :

Image

Remarque :  Pour écrire la relation de Chasles  , il n’y a pas besoin de regarder la figure.

Exercice : « E » , « N » , « K » étant trois points quelconques du plan.

Ecrivez toutes les égalités vectorielles possibles de la forme précédente .

 Exemple 1 :  

Exemple 2 :  

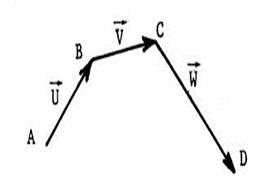
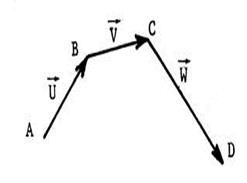
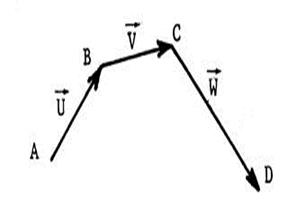
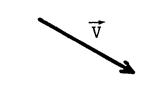
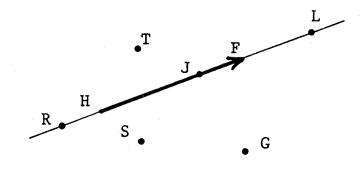
Ci-contre , un vecteur   et des points « S », « R », « T », « L »  , «  G » , « J » .

En utilisant successivement chacun de ces points , écrivez    sous forme de « 2 » vecteurs.

Généralisation :

Considérons trois points quelconques « M » , « N » , « P ».

On peut écrire    ( grâce à la relation de Chasles)

Quel que soit le point  « R »   ,     donc    et on peut continuer :

Quel que soit le point « S » ,  

Donc :                  et on peut continuer indéfiniment .

Théorème :

«  A , B , C , D , E , F » étant des points quelconques , on peut écrire par exemple :

image

Exercice 3 :

«  A , B , C , D » étant quatre points quelconques du plan, simplifiez les sommes ci-dessous de façon à n’avoir qu’un seul vecteur.

Fiche 5 : Exercices .

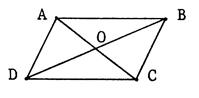
« ABCD »  est un parallélogramme de centre « O ».

Dans chacun des cas ci-dessous, on considère la somme de 2 vecteurs.

Vous allez déterminer, à l’aide des points de la figure, un représentant du vecteur égal à cette somme. Pour cela :

-        Passez en couleur les représentants de ces deux vecteurs sur le dessin.

-        Expliquez votre calcul ( colonne du centre).

-        Donnez votre résultat ( colonne de droite ).

-        Représentez le « vecteur-somme » sur le dessin . ( d’une autre couleur).

exemple

« ABCD »  est un parallélogramme , donc   

Donc   

Or :    ( relation de Chasles)

Donc