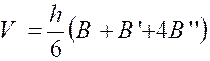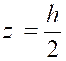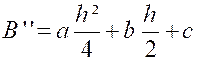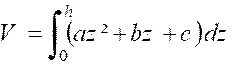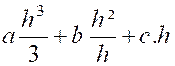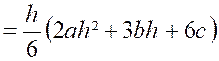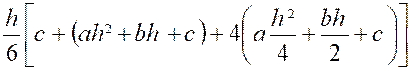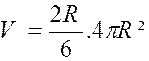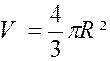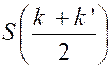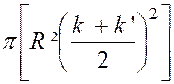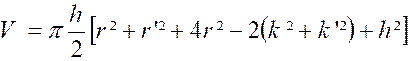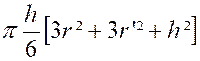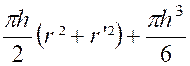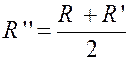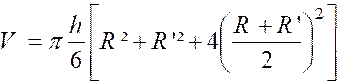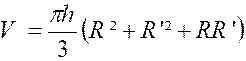Pré requis:
|
Info : liste des
connaissances en algèbre préparant au même concours. |
|
|
|
|
|
|
ENVIRONNEMENT du
dossier:
|
|
AVANT :
2°) Le calcul intégral. (niveau 4) 4°) L’intégration par parties. 5°) application géométrique
d’une intégrale simple :aires planes. |
APRES :
|
Complément
d’Info :
1°)
Liste des cours : prépa concours
A consulter pour
compléments : |
|
|
|
|
|
|
|
|
|
|
|
|
|
TITRE :niveau
III : LES INTEGRALES : APPLICATIONS GEOMETRIQUES DES INTEGRALES
SIMPLES :
VOLUME : FORMULE DES TROIS NIVEAUX .
|
|
1°)
Généralités. Remarque: La formule des trois niveaux s’applique aux
corps usuels : sphère , cylindre,cône et tronc de cône de
révolution,ellipsoïde,hyperboloïde et paraboloïde de révolution. |
|
|
|
2°)
Exemples : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Voir
l’évaluation !!! |
Contrôle |
évaluation |
|||
|
|
|
||
|
|
|
|
|
|
|
1°) Généralités. |
|
|
|
|
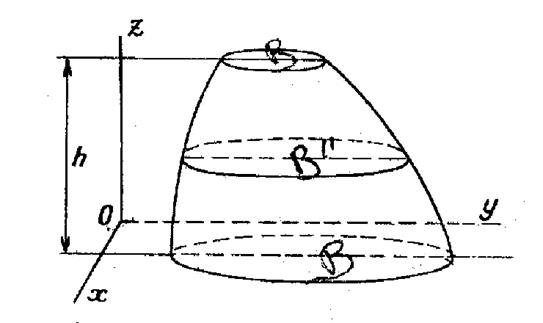
Considérons un trièdre de coordonnées
rectangulaires « 0 x ;y ;z » et
soit un volume tel qu’un plan de cote « z » ,le couple suivant une
section dont la surface est de la forme : « (voir
figure ci contre) On suppose ,de plus, que
le volume est limité à deux plans parallèles au plan « x 0 y ». Ces deux plans déterminent dans le solide des
bases « B » et « B’ ». Leur distance est la hauteur « h » du
volume à évaluer. |
|
|
|
|
Enfin ,
nous appelons « B ‘’ » la section faite dans le solide par un
plan équidistant des bases.. Ceci posé , nous allons
démontrer que le volume a pour valeur : |
|
|
|
|
Nous ne diminuons pas la généralité du problème
en supposant que la base inférieure est dans le plan « x 0 y ». Dans ces conditions, la base inférieure a pour
surface « B » la valeur de « S » pour « z =
0 », soit « B = C » ; de même « B’ »s’obtient
pour « z = h » «
B’ = a h² + b h +c » |
|
|
|
|
Et « B ‘’ » est la valeur de
« S (z) » pour « D’autre part, pour calculer « V » , partageons le
volume en petits éléments par des plans parallèles au plan « x O
y » . Chacun d’eux est assimilable à un cylindre ayant
pour base « S(z) » et pour hauteur « dz ». Par suite , le volume de
l’élément est : « Et le volume lui-même s’obtient en
intégrant : V = = |
|
|
|
|
Remarque 1 : Le même calcul a
déjà été fait à propos de la méthode de « Simpson ».(ici info…) Remarque 2 :
La formule des trois niveaux s’applique aux corps usuels : sphère , cylindre,cône
et tronc de cône de révolution,ellipsoïde,hyperboloïde et paraboloïde
de révolution. |
|
|
|
|
Exemple 1 : Volume de
la sphère. |
|
|
|
|
La hauteur « h » est le diamètre
« 2R » de la sphère ( voir
figure ci contre). Les bases extrêmes se réduisent à des points de
sorte que « B=0 » et « B’=0 ». La section faite par un
plan équidistant des bases est un grand cercle de surface « B’’= Le volume est par suite : La formule
|
|
|
|
|
|
|
|
|
|
Exemple 2 : Volume
du segment sphérique
. |
|
|
|
|
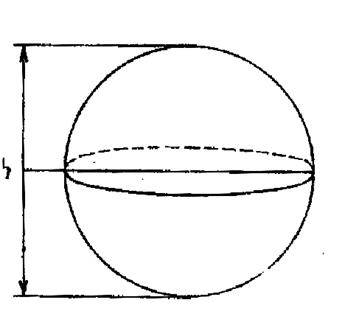
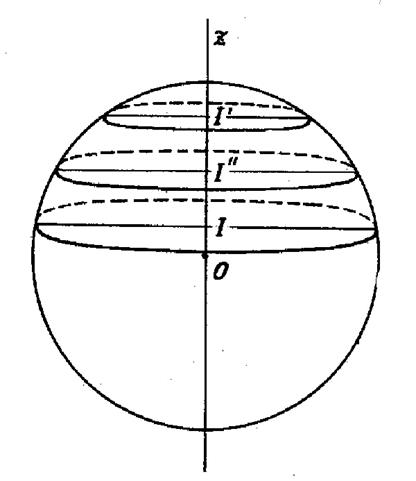
Soient « h » la hauteur ,
« r » et « r ’ »
les rayons des deux bases (voir figure ci contre) La
surface d’une section située à la distance « z » du centre
est :
« R » étant le rayon de la sphère . Désignons « k » et « k ‘ »
les côtes des deux bases : «
k = OI » et « K ‘ = O I
‘ » Nous avons par suite : « B = S ( k) = « B ‘ = S ( k ‘ ) = « B ‘ ‘ = |
|
|
|
|
D’autre part ,
l’identité : « ( k + k ‘)² +
( k² + k ‘ ² ) – h² » par suite
le volume du segment est :
|
|
|
|
|
Nous retrouvons bien le résultat élémentaire. Le volume du segment sphérique est égal à la demi- somme de deux cylindre
ayant pour base les deux bases du segment ,et même hauteur que lui , augmenté du volume
d’une sphère ayant pour diamètre la hauteur du segment. |
|
|
|
|
|
|
|
|
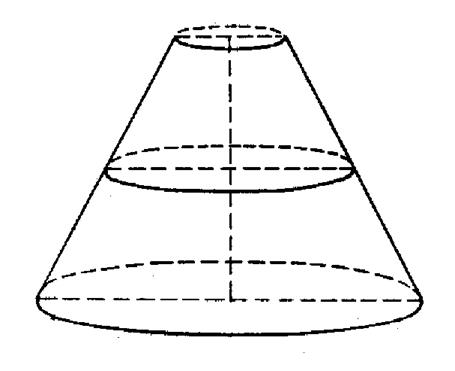
Exemple 3 :
Volume du tronc de cône. |
|
||
|
|
On nome la hauteur « h » , et les rayons des bases , « R » et « R ‘ ». Le rayon de la section équidistante est : Le volume est donc :
ce qui est la formule élémentaire !!!!! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CE qui termine ce cours………….. |
|
|
|
|
|
|
|
||
|
|
TRAVAUX AUTO FORMATIFS. |
||||
|
|
|
|
|||
|
|
CONTRÔLE |
|
|||
|
|
Voir le cours !!!!! |
|
|||
|
|
|
|
|||
|
|
EVALUATION :
|
||||
|
|
calculer : |
|
|||
|
|
Reprendre chaque exercice du cours. |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Voir le cours !!!!! |
|
|||