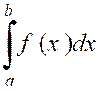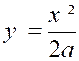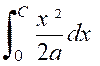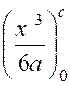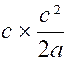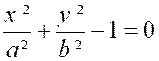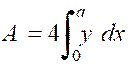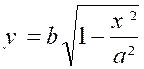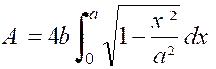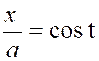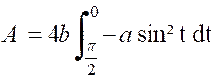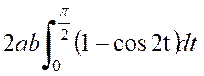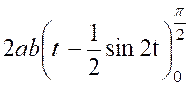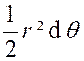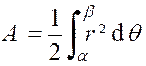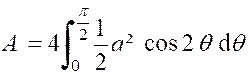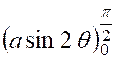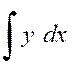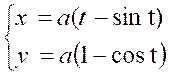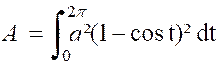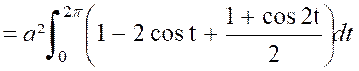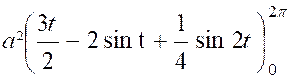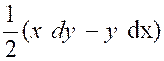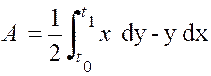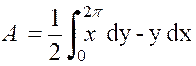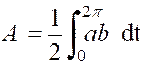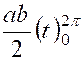1°) L’équation de la courbe est de la forme

2°)  La courbe est définie en coordonnées polaires.

3°) La courbe est définie par  des équations paramétriques.

COURS

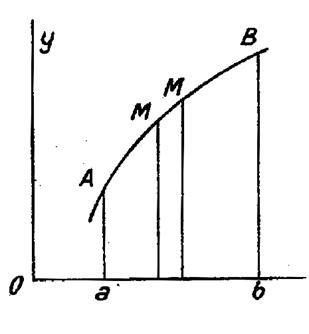
Pour évaluer l’aire limitée par une courbe plane ,il faut distinguer plusieurs cas suivant la manière dont la courbe est définie.

1°) l’équation de la courbe est de la forme

l’aire limitée par la courbe , l’axe « 0x » et les deux droites « x = a » et « x=b » est une intégrale définie ( voir ci contre).

Nous pouvons nous souvenir (voir   ici rappel « aire plane » )  que ceci revient à prendre pour élément d’aire,un « petit rectangle » ayant pour ordonnée «  » d’un point « M » et pour base l’accroissement «  » de l’abscisse.

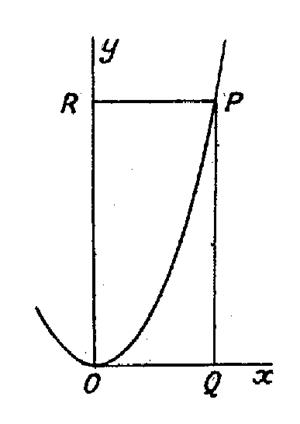
Exemple 1 :

(voir figure ci contre)

Soit l’équation de la parabole :

On demande : Evaluer  l’aire « OPQ » limité par la courbe, l’axe « Ox » et une droite « PQ » d’équation «  x = c ».

Comparer cette aire à celle du rectangle « R P Q O ».

Réponse :

L’aire  « OPQ »  =    =   = 

L’aire du rectangle = ( 0Q)(QP) =   = 

Pour comparer les deux aires on effectue le rapport :     /    =      .

Conclusion :   l’aire  « OPQ » est égale  à   de l’ aire  du rectangle « R P Q O ».

Exemple II .

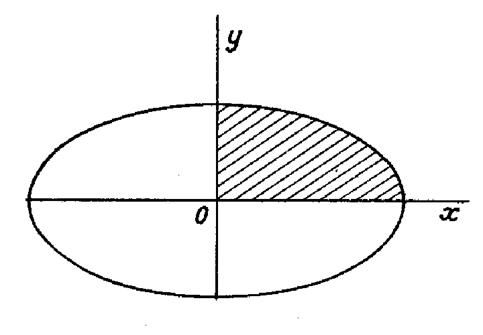
Calculer l’aire de l’ellipse : (voir figure ci contre)

«  »

la partie située dans le premier quadrant est le quart de l’aire totale,par symétrie.

L’aire de l’ ellipse est donc :  

De l’équation de la courbe, on tire :

Par suite :

Pour calculer cette intégrale , posons «  , d’où «  »

et        = =       = 

Info plus.

2°)  La courbe est définie en coordonnées polaires.

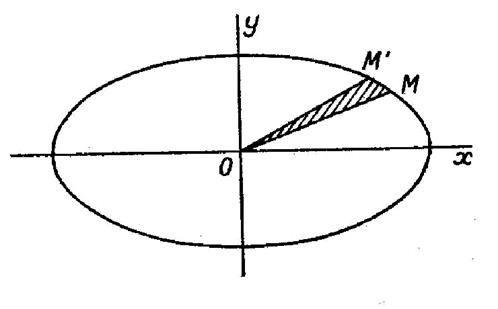
L’élément d’aire est le triangle « O M M’ » (figure ci contre)

La surface est (info +++)     :  .

La surface « A » comprise entre la courbe et deux rayons vecteurs d’angles polaires «  »  et  «  » s’obtient en intégrant : «  »

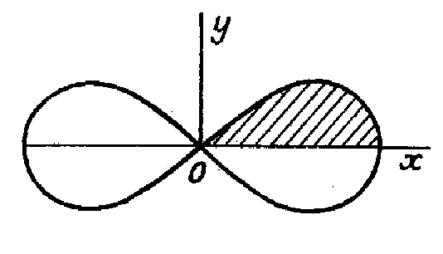
Exemple : Calculer l’aire de la lemniscate :    (voir figure ci contre)

La partie comprise dans le quadrant positif est le quart de l’aire totale « A » cherchée.

Par suite :   =  = a²

3°) La courbe est définie par  des équations paramétriques.

Si l’on cherche l’aire comprise entre la courbe ,l’axe « O x » et deux parallèles à « O y » : «  x = a » et « x = b », il faut calculer l’intégrale «  » dans laquelle on exprime en fonction du paramètre « t »

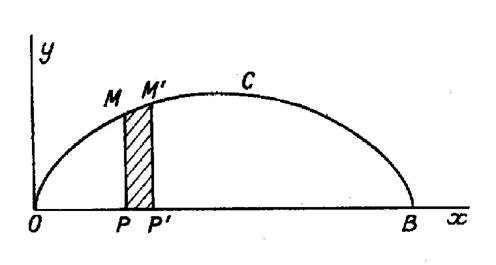
Exemple :  Calculer l’aire de la cycloïde .  ( voir figure ci contre)

L’élément d’aire est le rectangle de hauteur « PM » = « y » = « a ( 1 – cos t )» et la base « PP’ » =  « dx » = « a (1-cos t )».

par suite , l’aire limitée par la courbe « O C B » et l’axe « O x » est :

«  »

«A   ; A   =   ;  A  =

Ainsi :

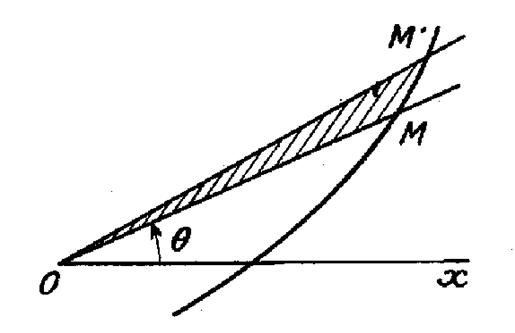
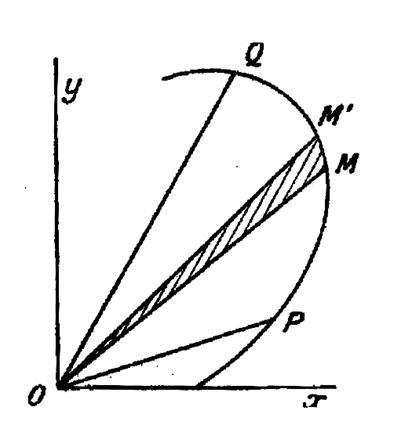
Si l’on veut connaître l’aire d’un secteur limité  par la courbe et deux rayons issus de l’origine  (voir figure ci contre)  on prend comme élément d’aire un petit rectangle tel que « OMM’ » .

Soient « x ; y » les coordonnées de « M » ; et   «  x + dx »  et « y + dy » celles de M ’.

La surface du triangle « M O M’ »est , au signe près ,

L’ aire  « OPQ » s’obtient en intégrant . Sa valeur est :

   ; l’intégrale étant prise entre les limites «  t ₀ » et « t ₁ » qui sont les paramètres des points « P » et « Q ».

Exemple :

Retrouvons , par ce procédé l’aire de l’ellipse  ( voir la figure ci contre).

 «  »

On peut définir l’ ellipse paramétriquement par les équations :

«  x = a cos t »     et «  y = b sin t »

La courbe est décrite entièrement lorsque « t » varie de « 0 » à «  »

D’où l’aire cherchée : 

On a «  »     et     «  »

  = 

par suite :   =    =   

CE qui termine  ce cours…………..

TRAVAUX AUTO FORMATIFS.

CONTRÔLE

Voir le cours !!!!!

EVALUATION :

calculer :

Reprendre chaque exercice du cours.

Voir le cours !!!!!