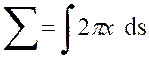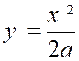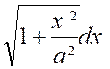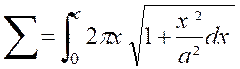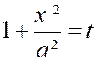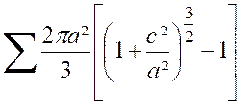Pré requis:
|
Info : liste
des connaissances en algèbre préparant au même concours. |
|
|
|
|
|
|
ENVIRONNEMENT du
dossier:
|
|
AVANT :
2°) Le calcul intégral. (niveau 4) 4°) L’intégration par parties. 5°) application
géométrique d’une intégrale simple :aires
planes. |
APRES :
|
Complément d’Info :
1°) Liste des cours : prépa concours
A consulter pour
compléments : |
|
|
|
|
|
|
|
TITRE :niveau
III : LES INTEGRALES : APPLICATIONS
GEOMETRIQUES DES INTEGRALES SIMPLES :
LES AIRES
DE REVOLUTION .
|
|
1°)
Généralités. Remarque: La formule des trois niveaux s’applique aux
corps usuels : sphère , cylindre,cône et tronc de cône de révolution,ellipsoïde,hyperboloïde
et paraboloïde de révolution. |
|
|
|
|
|
|
|
|
|
|||
|
Voir
l’évaluation !!! |
Applications :
Cours et fiches activités sur les aires et
les volumes |
Contrôle |
évaluation |
||
|
|
|
||
|
|
|
|
|
|
|
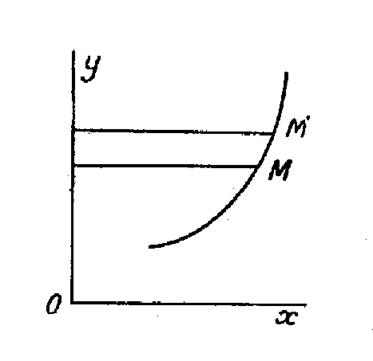
Soit une courbe tournant autour de l’axe « 0
y » (voir la figure ci contre). Nous avons déjà (cliquez ici ) que
l’élément d’aire est assimilable à un tronc de cône ayant pour surface
« Par suite l’aire totale est :
|
|
|
|
|
|
|
|
|
|
Exemple : |
|
|
|
|
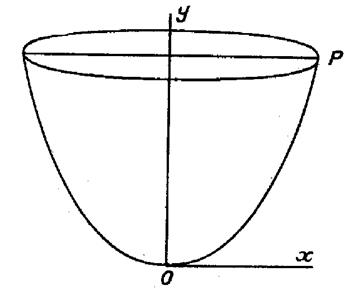
On donne l’équation de l’arc « OP » de la parabole : « On demande de calculer l’aire engendrée par cet
arc en tournant autour de l’axe « 0y ». Cette aire à pour valeur : |
|
|
|
|
D’autre part
( nous avons vu
déjà : cliquer ici) que On a donc : Pour intégrer on peut poser : On trouve, après tous calculs faits : |
|
|
|
|
|
|
|
|
|
CE qui termine ce cours………….. |
|
|
|
|
|
|
|
||
|
|
TRAVAUX AUTO FORMATIFS. |
||||
|
|
|
|
|||
|
|
CONTRÔLE |
|
|||
|
|
Voir le cours !!!!! |
|
|||
|
|
|
|
|||
|
|
EVALUATION :
|
||||
|
|
calculer : |
|
|||
|
|
Reprendre chaque exercice du cours. |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Voir le cours !!!!! |
|
|||