Index warmaths	Liste des leçons
	DOC : Elève.

IV) INFORMATIONS «  formation leçon » :

Test	COURS	Travaux auto - formation.			Corrigé des travaux auto - formation.
		Contrôle	évaluation	INTERDISCIPLINARITE	Corrigé Contrôle	Corrigé évaluation

Leçon	Titre
N°1/	Résumé Fiche 1 : Première équation algébrique

COURS

i9

A)) Idée d’une équation algébrique.

:i

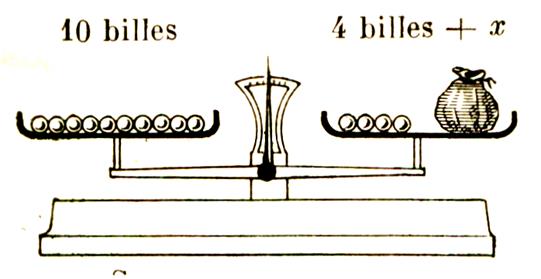
On dispose de billes en métal de même diamètre , de même masse.

Sur le plateau de gauche de la balance posons 10 billes. Sur le plateau de droite, posons quatre billes identiques et un sac contenant un nombre de (même) billes inconnu.

Supposons la balance en équilibre.

Représentons par la lettre « x » le nombre de billes du sac.

On peut dire que :

10 billes équilibrent 4 billes + « x » billes

On réécrit l’égalité :

Cette égalité

Est appelée « équation algébrique »

Une équation algébrique est une égalité qui comprend des « x » (appelés « inconnues »)

; Cette égalité peut s’écrire :

; est la forme simplifiée de l’égalité

i 1 9 et i 2 9

B) Quelques définitions

:i

Membres  et termes :

Dans une égalités il y a deux membres séparés par le signe « = »

Ainsi dans 10 = 4 + x ; 10 est appelé « premier membre »

4 + x est appelé « second membre »

Le second membre : « 4+x » deux quantités qui s’additionnent 4 et x . Ce sont deux termes.

Le premier membre :« 10 » ( ou (+10) » ne comporte qu’une quantité isolée. C’est encore un terme, 10 ; 4 ; x sont des termes.

Un terme est une quantité isolée ou une suite de termes précédés d’un signe + ou - ;

Remarque : dans la mesure du possible il est préférable de transformer une expression algébrique en une « somme algébrique »

Ainsi le nombre « 10 » devient le nombre relatif « (+10) » et 4+x devient la somme « (+4) + (x) »

10 et 4 sont des quantités numériques, on les appelle « termes connus »

« x » représente le nombre de billes inconnu .C’est un terme « inconnu » ou « terme en x ».

Dans une équation , Il y a donc deux sorte de termes : les termes en « x » et les termes connus.

En résumé :

Equation
10	=	4	+	x
Terme connu		Terme connu		Terme en « x »
1^er membre		2^ème membre

Ou

Equation
(+10)	=	(+4)	+	(x)
Terme connu		Terme connu		Terme en « x »
1^er membre		2^ème membre

Ecritures équivalentes

10 = 4 + x

Est la forme « simplifiée » de

(+10) = (+4) + (x)

i9

C) Quelques principes

:i

On utilise une balance dont on a équilibré les plateaux (on met l’aiguille à zéro)

Premier principe : Supposons qu’il y ait 30 billes sur chaque plateau. La balance se trouve en équilibre.

Si l’on ajoute 5 billes ou si l’on retranche 5 billes de chaque côté ( dans chaque plateau) , l’équilibre est maintenu , elle persiste.

On dira : que dans une égalité, on peut ajouter ou retrancher la même quantité aux deux membres d’une égalité sans détruire l’équilibre.

Deuxième principe : Reprenons l’équation 10 = 4 + x (1)

Enlevons  « 4 » à chaque membre :

Le premier membre devient : 10 - 4

Le second membre devient 4 + x - 4 , soit « x »

La nouvelle équation est 10 - 4 = x (2)

Comparons les équations (1) et (2)

Le « 4 » du second membre de l’équation (1) est passé dans le premier membre dans l’équation (2) . Mais il est devenu -4, c’est à dire qu’il a changé de signe.

Ainsi on peut dire : Dans une équation, on peut faire passer un terme d’un membre dans l’autre en changeant son signe.

Remarque : cette règle reste une « recette », à n’utiliser comme telle. Pour en savoir plus il faudra consulter l’objectif « neutraliser un terme dans un membre ».

i9

D) Résolution des équations.

:i

Reprenons la première équation : 10 = 4 + x

On fait passer « 4 » dans le premier membre en changeant de signe, on a : 10 - 4 = x

Soit x = 6

Le sac contient 6 billes.

On a ainsi trouvé la valeur de « x » de l’équation. Cette valeur « 6 » placée à la place de « x » dans l’équation de départ, vérifie que l’égalité numérique existe : 10 = 4 + 6 .

On dit qu’on a résolu l’équation.

Résoudre une équation , c’est rechercher par calcul (s) la valeur numérique de l’inconnue à partir de cette équation.

Quand « x » se trouve accompagné d’un terme connu, on l’isole en chassant le terme connu dans l’autre membre avec un signe contraire.

Autre exemple :

Résoudre 14 = x - 5 ; 14 + 5 = x ; x = 19

Leçon	Titre
N°1	TRAVAUX d ’ AUTO - FORMATION sur leçon N°1

TRAVAUX N° 1 d ’ AUTO - FORMATION : CONTROLE

1°) Qu’appelle-t-on « membre » ?

2°) Qu’appelle- t-on « terme » ?

3°) que signifie « Résoudre une équation » ?

4°) Compléter les phrases suivantes :

- On dira : que dans une égalité, on peut …………. ou ……………… la même quantité aux deux membres d’une égalité sans détruire l’équilibre.

- Ainsi on peut dire : Dans une équation, on peut faire passer un …………….. d’un membre dans l’autre en changeant s…… …………………….

TRAVAUX N° 1 d ‘ AUTO - FORMATION EVALUATION

Résoudre les équations suivantes :

1. a	X + 6 = 10	1. b	14 = 2 + x
2. a	X - 8 = 12	2. b	17= x -7
3. a	6 + x = 13	3. b	14= x+12
4. a	15 = 12 + x	4. b	X+ 12=13
5. a	13 = x - 2	5. b	x-10=1
6. a	11= 5 +x	6. b	7+x= 7
7. a	X + 8 = 12	7. b	12 = 1 + x
8. a	X - 13= 2	8. b	16 = x -15
9. a	6 + x = 9	9. b	11= x +11

N’est pas traité le cas ou « x » est précédé du signe « - » 

Exemple : 6 - x = 12 ( dans ce cas il faut faire passer « -x » dans l’autre membre !!!!!)

CORRIGE : Résoudre les équations suivantes :

10.a	X + 6 = 10 ; x = 4	10.b	14 = 2 + x ; x = 12
11. a	X - 8 = 12; x =20	11. b	17= x -7; x = 24
12.a	6 + x = 13; x = 7	12.b	14= x+12; x = 2
13.a	15 = 12 + x ; x = 3	13.b	X+ 12=13; x = 1
14.a	13 = x - 2; x = 15	14.b	x-10=1; x = 11
15.a	11= 5 +x; x = 6	15.b	7+x= 7; x = 0
16.a	X + 8 = 12; x = 4	16.b	12 = 1 + x; x = 11
17.a	X - 13= 2; x = 15	17.b	16 = x -15; x = 31
18.a	6 + x = 9; x = 3	18.b	11= x +11; x = 0