|
Auteur :
WARME R.
TRAVAUX ETUDE 1
du cours. Rechercher dans le
cours les informations.
|
|
Titre |
|
|
N°8 |
LES
TABLEAUX NUMERIQUES, le REPERAGE sur
une droite et dans un plan . |
corrigé de l ‘ ETUDE 1
DU COURS
ETUDE 1
« tableau »
Info :
Le
tableau numérique est utilisé en statistique ( exemple rangement et
classement de données) , en économie (exemple : facture), et dans les études de fonction
« mathématique ».
Dans
l’étude des fonctions : on rencontrera le tableau numérique
et le tableau dit de « variation » . Ces tableaux sont à remplir , ou a compléter . Les valeurs « contenues » vont permettre d’ identifier ou placer des « points » dans un
repère . ( voir le chapitre « 3 » de cette leçon.)
Dans
l’étude graphique d’une fonction : on reportera dans le tableau des
informations numériques (généralement
des coordonnées) qui sont
« caractéristiques ». ( voir le chapitre « 3 » de cette
leçon.)
Un
tableau numérique , à double entrées , en
particulier ; retiendra
notre attention lors de l’étude de la fonction linéaire ; on
l’appelle : tableau « de proportionnalité »
Compléter
la phrase :
Dans un
tableau numérique à simple entrée , une
information est obtenue par la lecture ………………………………………………
.
+Activité
n°1
On donne la répartition
des 204
élèves d’ un collège est :
58 en 3ème ;
74 en 5ème ; 59 en 4ème ; 65 en
6ème ; 18ème en classe pré professionnelle .
On demande de mettre ces
données dans un tableau à lecture
en ligne , puis à lecture en colonne .
Nota : les classes sont aussi appelées
« secteurs » .
Compléter
le tableau :
On peut reporter ces données
dans un tableau pour une lecture ……………………………………… :
|
Nom des
classes . (secteurs) |
Pré -
professionnelle |
En 6ème |
En 5ème |
En 4ème |
En 3ème |
|
Effectifs |
|
|
|
|
|
Tableau 2 : le compléter avec les données ci dessus.
On peut reporter ces données dans un
tableau pour une lecture ………………………………….. :
|
Nom des
classes : ( secteurs) |
Effectifs |
|
Pré - professionnelle |
|
|
En 6ème |
|
|
En 5ème |
|
|
En 4ème |
|
|
En 3ème |
|
Compléter
la phrase :
Dans ce
tableau à simple entrée, l’effectif d’un « secteur » apparaît dans
une ………………………… ,
au droit de la désignation, du secteur .
Tableaux 3 et
4
Autre exemple :
|
Corps
pur |
Fer |
Cuivre |
Argent |
Zinc |
Plomb |
Etain |
Eau |
Alcool |
|
Température de fusion ( °C) |
1535 |
1083 |
960 |
420 |
327 |
232 |
0 |
- 139 |
|
Température d’ébullition ( °C°) |
2750 |
2336 |
2000 |
907 |
1740 |
2270 |
100 |
79 |
Dire si le tableau ci dessus est un tableau est à
simple entrée ? à double
entrées ? un double tableau à
simple entrée ? R : …………………………………………..
Quelle la température de fusion du cuivre ?
…………………………….. ;
Quelle est la température d’ébullition du plomb
? ……………………..
Dans la liste proposée quel est le corps pur qui a la
plus grande température de
fusion ?........ ....
Dans la liste proposée quel est le corps pur qui a la
plus petit température d ‘ébullition
?...... .......
|
i9 |
I.2. Tableau
à double entrées |
Tableau 5
Dans le collège , les élèves garçons et filles se
répartissent de la façon suivante
. :
|
|
Filles |
Garçons |
Total |
|
Classe
pré professionnelle |
6 |
12 |
18 |
|
6ème |
36 |
29 |
65 |
|
5ème |
39 |
35 |
74 |
|
4ème |
35 |
24 |
59 |
|
3ème |
30 |
28 |
58 |
Exploitation du tableau 5 :
A quelle catégorie appartient l’effectif « 36 » ?
A quelle catégorie appartient l’effectif « 12 » ? .
A quelle catégorie appartient l’effectif « 28 » ?
Tableau 6
Les distances pour s’arrêter sont fonctions de la
vitesse ! ! ! !
Un véhicule
parcours 20 m pour s’arrêter
,s’il roulait à une vitesse de 20 km/h ;
Un véhicule
parcours 40 m pour s’arrêter
,s’il roulait à une vitesse de 40 km/h ;
Un véhicule parcours
80 m pour s’arrêter ,s’il roulait à une
vitesse de 60 km/h ;
Un véhicule
parcours 140 m pour s’arrêter
,s’il roulait à une vitesse de 80 km/h ; …………
Un véhicule
parcours 220 m pour s’arrêter
,s’il roulait à une vitesse de 100 km/h ; …………
Un véhicule
parcours 320 m pour s’arrêter
,s’il roulait à une vitesse de 120 km/h ; …………
Construire le tableau
Ce qui
permet de construire le tableau :
|
Vitesse
en Km/h |
20 |
40 |
60 |
80 |
100 |
120 |
|
Distance
(m) |
|
|
|
|
|
|
Q :
Traduire ce qui peut être lu dans la 5ème colonne :
Tableau 7
Un libraire solde des cahiers en les
vendant par lots de « 3 ».Un lot de « 3 » cahiers est
vendu 5 €.
Compléter le
tableau .
|
Nombre
de lots |
1 |
4 |
6 |
7 |
10 |
|
Prix ( en €) |
|
|
|
|
|
Q :
Comment obtient -on une information dans un tableau à double
entrée ?
Tableau 8
1°) Soit l’extrait d’un relevé de
compte : ( en € )
|
Date |
Valeur |
Nature des opérations |
Débit - |
Crédit + |
|
Ancien solde au 28/04 /200.. |
|
8 411,38 |
||
|
01/04 |
30/ 03 |
Facture CB du 28/03/ |
29,58 |
|
|
01/04 |
01 / 04 |
Retrait guichet |
259,16 |
|
|
04/04 |
03/04 |
Paiement av. prélèvement .Trésor
public 80 impôt |
137,36 |
|
|
10/04 |
09/04 |
EDF Prélèvement pays de l’A |
15,23 |
|
|
13/04 |
12/04 |
Virement faveur du compte . |
|
259,16 |
|
21/ 04 |
08/04 |
Votre chèque n°………. |
14,94 |
|
|
21/04 |
19/04 |
Facture CB du 19/04 |
335,39 |
|
|
28/04 |
29/04 |
Virement TPG Somme Paye |
|
1 884,86 |
|
|
|
|||
Questions :
1°) Mettre le signe plus ou moins devant chaque
opération ( débit = - , crédit = +)
_ 8411,38 ; _ 29, 58 ; _ 259,16 ; _ 137,36 ; _
15,23 ; _ 259,16 ; _ 14,94 ; _ 335,39 ; _ 1884 , 86 .
2°)Calculer le montant total des
débits .
3°) Calculer le montant total des crédits .
4°)Calculer le montant du nouveau
solde avant virement du salaire au 29
/ 04
( Ce
travail faisant suite au cours sur
les nombres relatifs )
|
Cd : Info
plus ! ! |
Donner la définition d’un axe :
De quoi est -
il muni ? précisez .
Comment construit - on une
graduation ?

Exercice 1 : qu’elle est
l’abscisse du point M ? .
A chaque point M de l’axe
correspond un et un seul nombre
relatif noté xM . Ce nombre
est l’ abscisse de M .
Exercice 2
On donne les coordonnée des
points M ( 0,5) ; N ( -2) et P ( 2,25) ,
On demande de les placer sur la droite
graduée :
|
|
|
|
+ Exercice 3
On
donne des points sur une
droite A , B , C et un segment unitaire (O,I);
Graduer la droite et donner les abscisses
de ces points.
|
|
|
|
+ Exercice 4 : Recherche de l’origine d’un repère
connaissant la position de deux points
Enoncé du problème :
Soient 2 points A et B .
On donne leurs abscisses :
on appelle : x
A ( = +1,5
) l’abscisse du point A
et on appelle x B ( = - 5,5 ) l’abscisse du point B
Noter sur l’axe, , après avoir fait le calcul nécessaire , la position de l’origine O de la graduation.
|
|
Donner la procédure de
calcul :
|
III. REPERAGE
DANS UN PLAN. |
Cd :Info
N°1plus ! ;Cd : Info
N°2 plus ! |
Compléter
les phrases suivantes :
1.
Pour repérer un point sur une ligne il faut connaître ……………………………. ( ou ……….
dimension). : « x »
2.
Pour repérer un point dans un plan il faut connaître ……………………………… ( ou ………….
dimensions). : « x ;
y »
3.
Pour repérer un point dans l’espace il faut connaître …………………………… ( ou …………. dimensions).
« x ; y ; z »
4 .
Le repère que l’on utilise est appelé
aussi : « repère ………………………………… » ;
( venant du mathématicien
« Descartes »)
1°
) nomenclature :
Dans un
repère ( O , I , J )
du plan , d’axes ( x’ O x )
et ( y’ O y ) perpendiculaires , chaque point tel que « M » est repéré par ses ……………………….. :
Que désigne x M ?
Que désigne
y M . ?
= x M et y
M sont des nombres …………………….
=On notera : M ( x M ; y M )
|
Représenter
dans un repère cartésien un point M ; Placer : ( O , I , J )
nommer les axes , repérer les coordonnées de ce points. |
|
=Les coordonnées d’un point
dans un repère du plan sont des nombres relatifs ; ils peuvent
être ……………………………………...
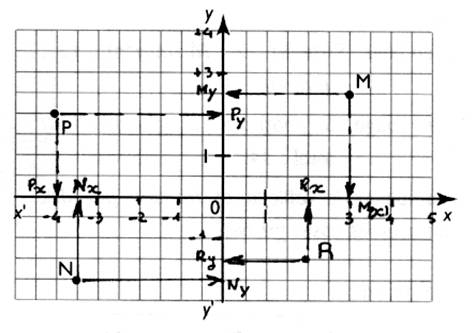
2°) +Activité n° 9
On
place dans un repère cartésien des
points : ( M , P , N, R )
|
|
On en
déduit les informations suivantes :
Compléter le tableau ci dessous :
|
|
Abscisse |
Ordonnée |
Coordonnées |
Nota |
|
M |
|
|
|
|
|
P |
|
|
|
|
|
N |
|
|
|
|
|
R |
|
|
|
|
|
i |
||
|
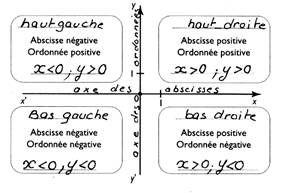
Zones |
Points |
Tracer un repère cartésien
possédant les 4 zones et
placer les points dans la zone correspondante |
|
x <0 ; y > 0 |
R |
|
|
x>0 ; y < 0 |
S |
|
|
x
> 0 ; y > 0 |
T |
|
|
x<0 ; y < 0 |
V |
|
|
3
- Abscisse du milieu d’un segment sur
un axe |
Soit une droite graduée , un point « O » d ‘ abscisse
« 0 » , un point
« I » d ‘abscisse
« 1 » , un point « A » d ‘abscisse « xA » et un point « B » d ‘«
abscisse « xB »

Devoir 1 /2 :
Quel calcul faut -il faire pour connaître l’ abscisse
du point M milieu du segment AB ?
Etablir une
formule :
Formation
niveau V : On doit savoir représenter ou à reconnaître les fonctions. dites « linéaires » et les
fonctions dites « affines ». dans un repère
cartésien
Et savoir identifier ces
fonctions par l’écriture (forme) de leur
équation : la fonction linéaire
à une équation de la forme : y = a x ; la fonction affine à une équation de
la forme y = a x + b .
Informations : Pour
repérer un point il faut 2 valeurs : une appelée « x » et l’autre « y » .
La valeur de « y » est obtenue en fonction de la valeur de
« x » que l’on notera
: y = f ( x ) ;
. Les coordonnées d’un point se
noteront : ( x ; y ) ou (
x ; f(x))
La représentation graphique d’une fonction notée « f(x) »
dans un repère est un ensemble de points
dont de coordonnées ( x ; y
) ; , ces valeurs placées dans l’ordre
permettront de placer chaque point
dans un repère dit
« cartésien » .
Pour
faire cette représentation graphique d’une fonction on a besoin d’une équation
mathématique .
C’est à
partir de cette équation , que l’on calculera la valeur de l’ordonnée ( y
) d ‘ un point
. On déterminera ( ou on
attribuera ) une valeur à
« x » , pour obtenir la valeur de « y » correspondante
.
Pour obtenir les coordonnées d’un point , on
se fixe donc une valeur de l’abscisse « x » ( valeur qui est donnée ou choisie) ,
pour trouver la valeur de l’ordonnée .
Les
valeur de « x » sont soit données ; soit choisies .
En règle générale on choisit des valeurs de
« x » comprises entre une valeur mini et une valeur max. fixées au
préalable , ces valeurs s’appellent « bornes ».
Par exemple : on peut décider
de connaître le tracé d’une fonction , pour des valeurs de x
= [ 0 ; 4 ] ; ( on peut écrire pour des valeurs de
« x » : 0 £ x £ + 4 )
Au niveau V ; on aura une équation ,un
tableau à remplir , ( généralement on nous fixe les valeurs de
« x » ; il faut trouver ,
par calcul , les valeurs « y » .Il reste ensuite à reporter les
points à l’aide des coordonnées dans un repère . ( ce repère
est : soit donné , soit à
construire soit même ) .
La fonction linéaire à une
équation de la forme : y = …………. ; la
fonction affine à une équation de la forme y = …………………
.
La représentation graphique
de la fonction linéaire est une droite passant par « 0 ».
La représentation graphique
de la fonction affine est une droite qui
ne passe pas par « 0 ».
Les droites parallèles
aux axes ne sont ni linéaire ni affine.
Compléter les phrases suivantes :
|
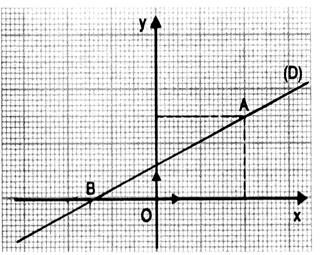
Ci dessous : on vous a tracé une droite passant par
« O » ; toutes les droites passant par « 0 »
sont les représentantes des fonctions dites « ……………………» |
Ci dessous : on vous a tracé une droite ne passant pas par « O » ; toutes
les droites ne passant pas par « 0 » sont les représentantes des
fonctions dites « ……………. » |
|
|
|
La fonction linéaire à une
équation de la forme : y = …………. ; la
fonction affine à une équation de la forme y = ……………
.
La représentation graphique
de la fonction linéaire est une droite passant par « ……………… ».
La représentation graphique
de la fonction affine est une droite qui
ne passe pas par « …………… ».
Les droites parallèles
aux axes ne sont ni linéaire ni affine.
|
On
trouvera , comme ci dessous ,des droites parallèles à l’axe des
« x » |
On
trouvera , comme ci dessous , des droites parallèles à l’axe des
« y » |
|
|
|
|
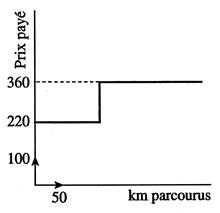
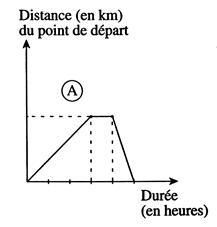
Que se
passe - t- il à 150 km. |
Interpréter le
tracé : |
Des
exercices de ce type sont donnés à
analyser dans les travaux auto formatifs.
+Exercice :
Représenter une fonction dans un repère.
Définition :
La
représentation graphique d’une fonction f dans un repère est constitué par tous
les points dont les coordonnées sont (
x ; y ) ou , puisque y = f(x)
; ( x ; f(x))
Exemples :
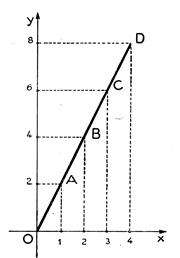
1°) On veut représenter
graphiquement la fonction dont l’équation est f1 (x) =
2,5 x pour des
valeurs de x comprises entre 0 et 4.
On demande de
remplir le tableau suivant : ( il faut calculer pour chaque point sa valeur
« y »)
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
|
x |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
|
f1(x)
( = y) |
? |
? |
? |
? |
? |
? |
? |
? |
? |
On donne le papier millimétré
suivant : on demande de placer les points « A….., » après avoir calculer pour chacun ses
coordonnées
|
|